用线性回归模型预测房价

本文使用sklearn 中自带的波士顿房价数据集来训练模型，然后利用模型来预测房价。这份收据中共收集了13个特征。

1.输入特征

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_boston

boston = load_boston()
X = boston.data
y = boston.target
X.shape

输出为：“(506,13)”共有506个样本 13个特征。

print(X[0])
输出结果为：
array([  6.32000000e-03,   1.80000000e+01,   2.31000000e+00,
         0.00000000e+00,   5.38000000e-01,   6.57500000e+00,
         6.52000000e+01,   4.09000000e+00,   1.00000000e+00,
         2.96000000e+02,   1.53000000e+01,   3.96900000e+02,
         4.98000000e+00])

可以通过boston.feature_names 来查看这些特征的标签

array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
       'TAX', 'PTRATIO', 'B', 'LSTAT'], 
      dtype='|S7')

2.模型训练

LinearRegression 类实现了线性回归算法。在训练之前先把数据集分为两份。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3)

训练模型并测试模型准确性

import time
from sklearn.linear_model import LinearRegression

model = LinearRegression()

start = time.clock()
model.fit(X_train, y_train)

train_score = model.score(X_train, y_train)
cv_score = model.score(X_test, y_test)
print('elaspe: {0:.6f}; train_score: {1:0.6f}; cv_score: {2:.6f}'.format(time.clock()-start, train_score, cv_score))

统计了模型的训练时间，统计模型对训练样本的准确性得分（即对训练样本的拟合好坏程度）train_score,还统计了模型对测试样本的得分 cv_score
运行结果如下：

elaspe: 0.002447; train_score: 0.723941; cv_score: 0.794958

从结果可以看出模型拟合效果一般。

3.模型优化

模型优化的方式
1.观察特征的变化范围从$10^{-3}$级别到$10^2$,先将数据进行归一化的处理，可以加快算法的收敛速度。
2.增加多项式特征

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

def polynomial_model(degree=1):
    polynomial_features = PolynomialFeatures(degree=degree,
                                             include_bias=False)
    linear_regression = LinearRegression(normalize=True)
    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression)])
    return pipeline

接着我们使用二阶多项式来你和数据：

model = polynomial_model(degree=2)

start = time.clock()
model.fit(X_train, y_train)

train_score = model.score(X_train, y_train)
cv_score = model.score(X_test, y_test)
print('elaspe: {0:.6f}; train_score: {1:0.6f}; cv_score: {2:.6f}'.format(time.clock()-start, train_score, cv_score))

输出结果是：

elaspe: 0.016412; train_score: 0.930547; cv_score: 0.860465

训练样本分数和测试样本分数都提高了，模型得到了优化。
把多项式特征改为三阶查看效果。
运行结果为 ：

elaspe: 0.133220; train_score: 1.000000; cv_score: -105.517016

针对训练样本的分数达到了1 ，而对测试样本的分数却是负数，产生了过拟合。

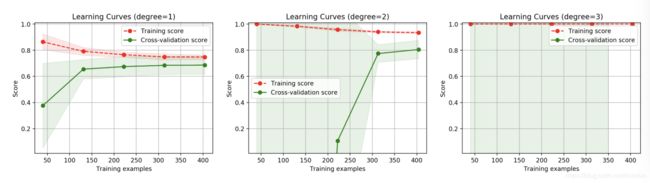
4.学习曲线

通过画出学习曲线，来对模型的状态及优化的方向直观的观察。

from common.utils import plot_learning_curve
from sklearn.model_selection import ShuffleSplit

cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
plt.figure(figsize=(18, 4), dpi=200)
title = 'Learning Curves (degree={0})'
degrees = [1, 2, 3]

start = time.clock()
plt.figure(figsize=(18, 4), dpi=200)
for i in range(len(degrees)):
    plt.subplot(1, 3, i + 1)
    plot_learning_curve(plt, polynomial_model(degrees[i]), title.format(degrees[i]), X, y, ylim=(0.01, 1.01), cv=cv)

print('elaspe: {0:.6f}'.format(time.clock()-start))