【sklearn】SVM（支持向量机） - 预测在网具有单卡转合约倾向的客户

训练数据

本实验的特征维度取自实际工程，但具体数据纯属模拟，只是想以此对SVM理论进行一次实践。

数据集-数据字典

序号	名称	说明	类型	备注
1	user_id	用户标识	int
2	service_kind	业务类型	string	2G、3G、4G
3	call_duration	主叫时长（分）	double
4	called_duration	被叫时长（分）	double
5	in_package_flux	免费流量	double
6	in_package_flux	计费流量	double
7	month_duration	月均上网时长（分）	double
8	net_duration	入网时长（天）	long
9	last_recharge_value	最近一次缴费金额（元）	double
10	total_recharge_value	总缴费金额（元）	double
11	total_recharge_count	缴费次数	int
12	contractuser_flag	是否潜在合约用户	int	1：是， 0：不是

 

SVM介绍

支持向量机属于监督学习类算法，在解决小样本，非线性以及高维识别问题时有很大优势。

sklearn模块中SVM算法参数介绍：

def __init__(self, C=1.0, kernel='rbf', degree=3, gamma='auto_deprecated',
                 coef0=0.0, shrinking=True, probability=False,
                 tol=1e-3, cache_size=200, class_weight=None,
                 verbose=False, max_iter=-1, decision_function_shape='ovr',
                 random_state=None):

1. C：惩罚参数，默认值是1.0. C越大， 相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时的准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。
2. kernel：核函数，默认是rbf，可以是linear，poly，rbf，sigmoid，precomputed；其中0代表线性，1代表多项式，2代表RBF函数，3代表sigmoid
3. degree：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略
4. gamma：rbf，poly和sigmoid的核函数参数。默认是auto，否则会选择1/n_features。gamma参数越高，模型越复杂
5. coef()：核函数的常数项。对于‘poly’和‘sigmoid’有用
6. probability：是否采用概率估计，默认为false
7. shrinking：是否采用shrinking heuristic方法，默认为true
8. tol：停止训练的误差值大小，默认为1e-3
9. cache_size：核函数cache缓存大小，默认为200
10. class_weight：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)
11. verbose：允许冗余输出
12. max_iter：最大迭代次数。-1为无限制
13. decision_function_shape：‘ovo’，‘ovr’ or None
14. random_state：数据洗牌是的种子值，int值

代码实现

模块导入：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn import datasets

from sklearn import svm, metrics  # metrics用于评估模型，例如正确率、召回率等
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV  # 基于网格搜索交叉验证
from sklearn.preprocessing import OneHotEncoder  # 文本转换为数值特征

from pylab import mpl

mpl.rcParams['font.sans-serif'] = ['FangSong']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号‘-’显示为方块的问题

数据读取：

# 读取数据
data = pd.read_csv('./data_carrier_svm.csv', encoding='utf8')
data.head()

 

数据分布状态探索：

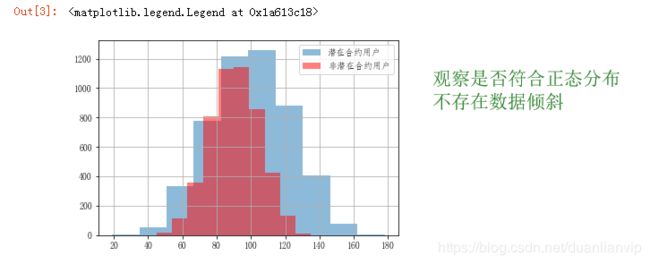
# 不同用户的主叫时长分布情况对比
cond = data['是否潜在合约用户'] == 1  # 若为潜在合约用户，cond=true，否则cond=false
data[cond]['主叫时长（分）'].hist(alpha=0.5, label='潜在合约用户')  # 把潜在合约用户的“主叫时长”使用直方图画出，alpha设置透明度，0为完全透明
data[~cond]['主叫时长（分）'].hist(color='r', alpha=0.5, label='非潜在合约用户')  # 把非潜在合约用户的“主叫时长”使用直方图画出
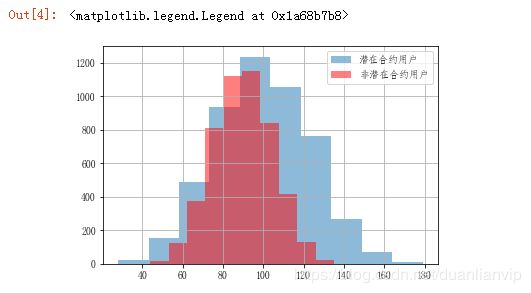
plt.legend()

 

# 不同用户的被叫时长分布情况对比
cond = data['是否潜在合约用户'] == 1
data[cond]['被叫时长（分）'].hist(alpha=0.5, label='潜在合约用户')
data[~cond]['被叫时长（分）'].hist(color='r', alpha=0.5, label='非潜在合约用户')
plt.legend()

# 不同用户的业务类型情况对比
grouped = data.groupby(['是否潜在合约用户', '业务类型'])['用户标识'].count().unstack()  # 对'是否潜在合约用户'和'业务类型'按照‘用户标识’进行统计个数，类似于SQL语句的group by操作
print(grouped)
grouped.plot(kind='bar', alpha=1.0, rot=0)  # rot可以控制轴标签的旋转度数

# 统计各类数据的数量
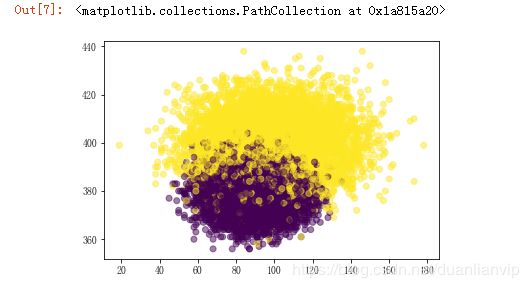
data['是否潜在合约用户'].value_counts()

# 生成数据可视化
y = data.loc[:, '是否潜在合约用户'] # y为标签值，即“是否潜在合约用户”列
plt.scatter(data.loc[:, '主叫时长（分）'], data.loc[:, '免费流量'], c=y, alpha=0.5)  # 散点图，x轴为 '主叫时长（分）'，y轴为'免费流量'

数据预处理：

# 分割特征数据集和便签数据集
X = data.loc[:, '业务类型': '余额']  # 特征
y = data.loc[:, '是否潜在合约用户']  # 标签
print('The shape of X is {0}'.format(X.shape))
print('The shape of y is {0}'.format(y.shape))

X.head()

 

# 自定义转换函数
def service_mapping(cell):
    if cell == '2G':
        return 2
    elif cell == '3G':
        return 3
    elif cell == '4G':
        return 4


# 将业务类型的string型值映射为整数型
service_map = X['业务类型'].map(service_mapping)
service = pd.DataFrame(service_map)  # DataFrame是Python中Pandas库中的一种数据结构，它类似excel，是一种二维表

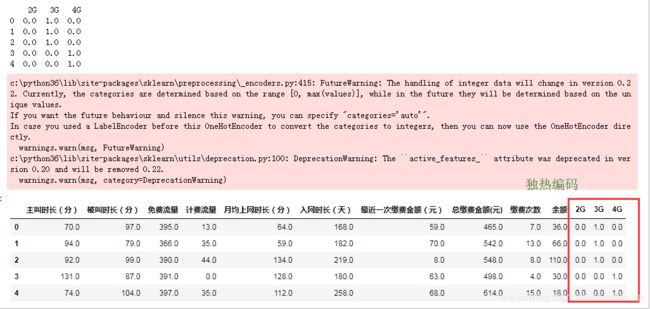
# 使用OneHotEncoder转化类型特征为0/1编码的多维特征
enc = OneHotEncoder()
service_enc = enc.fit_transform(service).toarray()  # service_enc的形状为(10000, 3)的独热编码，例：3G-->[0. 1. 0.]

# 0/1编码的多维特征的名称
service_names = enc.active_features_.tolist()  # service_names为[2, 3, 4]
service_newname = [str(x) + 'G' for x in service_names]  # service_newname为['2G', '3G', '4G']

service_df = pd.DataFrame(service_enc, columns=service_newname)  # service_df形状为(10000, 3)
print(service_df.head())  # 显示前5行
X_enc = pd.concat([X, service_df], axis=1).drop('业务类型', axis=1)  # 追加经过编码转换后的“2G”“3G”“4G”列，从DataFrame中删除“业务类型”列
X_enc.head()

# 数据归一化/正则化
from sklearn.preprocessing import normalize
'''
一般涉及到梯度下降和距离的计算需要进行标准化或正则化。例如Logistic Regression、SVM、PCA等。

标准化是常用的机器学习特征处理的方法，它可以将一列数据的平均值变为0，方差变为1 。改变原来的数据结构分布，将数值进行缩放。使得所有特征在同一量纲下进行数据处理，避免有些特征整体偏大对整体处理造成偏差。
标准化针对的是把整列(特征)作为处理对象，而正则化把行(样本)作为处理对象。
标准化=（原值-均值）/标准差。得到的结果是，对于每个特征（每列），他们的平均值为0，方差为1。

正则化针对的是每行，或者说每个样本的不同特征。一般计算样本之间距离时使用其做归一化处理，比如聚类，K近邻、文本分类。
正则化的过程是将每个样本缩放到单位范数。

sklearn.preprocessing.normalizer(norm='l2', copy=True)
norm：可以为l1、l2或max，默认为l2
若为l1时，样本各个特征值除以各个特征值的绝对值之和。特征值除以其所在行的所有特征值绝对值之和
若为l2时，样本各个特征值除以各个特征值的平方之和的平方根
若为max时，样本各个特征值除以样本中特征值最大的值
'''
X_normalized = normalize(X_enc)
X_normalized

# 分割训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_normalized, y, test_size=0.2, random_state=112)
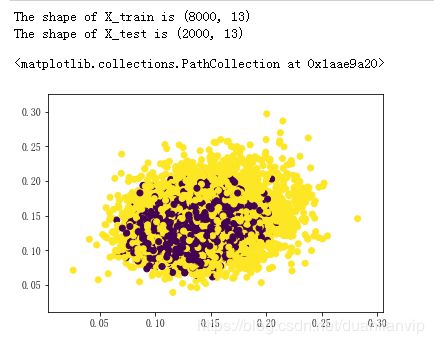
print('The shape of X_train is {0}'.format(X_train.shape))
print('The shape of X_test is {0}'.format(X_test.shape))

# 生成数据可视化
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train)  # X_train[:, 0]：第一列数据，即“主叫时长（分）”； X_train[:, 1]：第二列数据，即“被叫时长（分）”；y_train:训练集标签

 

 

# 模型实例化
linear_clf = svm.LinearSVC()  # LinearSVC支持向量分类器
# 在训练集上训练模型
linear_clf.fit(X_train, y_train)

# 在测试集上预测
y_pred = linear_clf.predict(X_test)  # # 返回预测标签

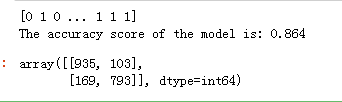
# 计算准确率
score = metrics.accuracy_score(y_test, y_pred)
print('The accuracy score of the model is: {0}'.format(score))

# 查看混淆矩阵
metrics.confusion_matrix(y_test, y_pred)  # 也称误差矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示

# 调试参数，设置调试参数的范围
C_range = np.logspace(-5, 5, 5)  # 惩罚参数
gamma_range = np.logspace(-9, 2, 10)
clf = svm.SVC(kernel='rbf', cache_size=1000, random_state=117)  # cache_size：核函数cache缓存大小，默认为200
param_grid = {'C': C_range, 'gamma': gamma_range}

# GridSearch作用在训练集上
grid = GridSearchCV(clf, param_grid=param_grid, scoring='accuracy', n_jobs=2, cv=5)
grid.fit(X_train, y_train)

# 得到最优参数
print(grid.best_score_)
print(grid.best_params_)
print(grid.best_estimator_)

利用最优参数重新在整个训练集上训练模型，并利用该模型在测试集上进行预测。

# 训练参数调优后的模型
clf_best = svm.SVC(kernel='rbf', C=grid.best_params_['C'], gamma=grid.best_params_['gamma'], probability=True)
# fit on the trainingt data
clf_best.fit(X_train, y_train)
# predict on the testing data
y2_pred = clf_best.predict(X_test)

# 模型评估，模型预测结果估计：精确度和混淆矩阵
accuracy = metrics.accuracy_score(y_test, y2_pred)
print('The accuracy is %f' % accuracy)

# get the confusion matrics
# 混淆矩阵就是分别统计分类模型归错类，归对类的观测值个数，然后把结果放在一个表里展示出来。这个表就是混淆矩阵
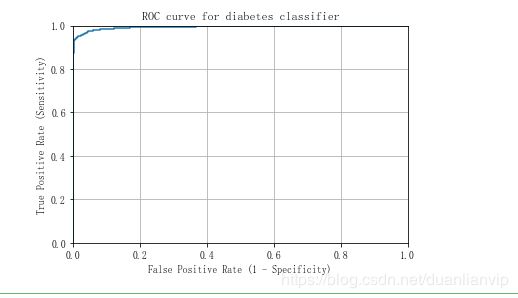
metrics.confusion_matrix(y_test, y2_pred)

# 模型效果评估：roc曲线，roc曲线越趋近于左上角，预测结果越准确
# store the predicted probabilities for class 1
y2_pred_prob = clf_best.predict_proba(X_test)[:, 1]  # 返回预测属于某标签的概率

# IMPORTANT: first argument is true values, second argument is predicted probabilities
# fpr: false positive rate (= 1 - specifity ),  tpr = true postive rate
fpr, tpr, thresholds = metrics.roc_curve(y_test, y2_pred_prob)  # fpr和tpr就是混淆矩阵中的FP和TP的值,thresholds就是y_score逆序排列后的结果
# plt.plot(x,y,format_string,**kwargs) x轴数据，y轴数据，format_string控制曲线的格式字串,format_string 由颜色字符，风格字符，和标记字符 
plt.plot(fpr, tpr)
plt.xlim([0.0, 1.0])  # 设置参数范围
plt.ylim([0.0, 1.0])
plt.title('ROC curve for diabetes classifier')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.grid(True) # 生成网格

 

参考

1. https://blog.csdn.net/kancy110/article/details/75050026#commentsedit
2. https://blog.csdn.net/sscc_learning/article/details/73692374#commentBox
3. https://blog.csdn.net/Orange_Spotty_Cat/article/details/80520839
4. https://www.cnblogs.com/mrtop/p/10309083.html