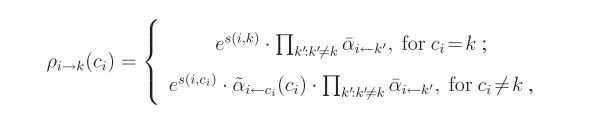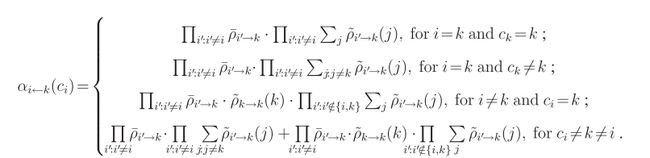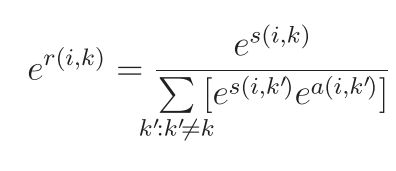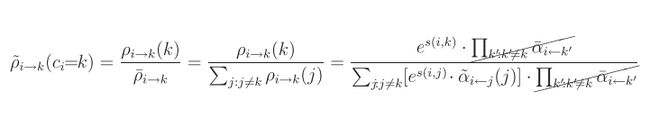Affinity propagation 近邻传播算法

终日乾乾，与时偕行。 — 周易 ⋅ 乾 ⋅ 文言

近邻传播算法是一种基于代表点的聚类方法，它会同时考虑所有数据点都是潜在的代表点，通过结点之间的信息传递，最后得到高质量的聚类。这个信息的传递，是基于sum-product或者说max-product的更新原则，在任意一个时刻，这个信息幅度都代表着近邻的程度，也就是一个数据点选择另一个数据点作为代表点有多靠谱。这也是近邻传播名字的由来。

近邻传播算法输入的信息是一个实值的集合， {s(i,k)} ，每个相似度 s(i,k) 都代表着一个数据k有多适合作为另一个数据i的代表点，可以看成是它们本身的相似度。每一个数据点都有一个对应的变量结点 ci ,其中，如果 ci=k 而 i≠k 就代表着数据点i已经分配给了一个聚类， ck 是它的代表点。 ck=k 就是说数据点k本身就是一个聚类代表点。我们可以构造一张图，用带约束的网相似度（net similarity）来作为图的函数。
图的结构如下：

其中方格的代表函数结点，圆圈代表变量结点。我们定义网相似度如下：

这是带有约束的，其中第一项是k-median 问题演化过来的（也比较好理解，每个点i都和它的代表点的相似度最高），只不过将它放在自然指数的位置，这是为了保证我们的 F(c,s) 总是正数。第二项添加了一致性约束，就是说如果有非k的结点选了k作为代表点，那么k必须同时是本身的代表点。否则就会有惩罚。

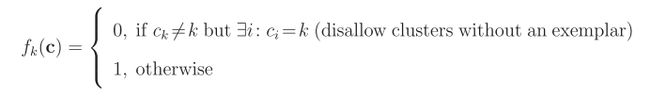
F(c,s) 的两项都各自通过一个函数结点来表示，而标签值（聚类类别值） ci 用一个变量结点来表示。 log F(c,s) 可以写成log函数的sum的形式。

1. Sum-Product Affinity Propagation

我们可以用sum-product 算法来得到变量的组合以完成对 F(c;s) 的最大化，同时这也是对 eS(c) 的最大化。 S(c) 这里是带有约束的。对于这种特殊的图拓扑，使用sum-product 是非常直接的，通过变量结点到函数结点的信息传递，以及函数结点到变量结点的信息传递可以实现。

O(NN) 向量信息更新

从变量结点 ci 到函数结点 fk(c) 包含了N个非负的实值——其中每一个的取值为j( ci 中的一个取值，也就是说是从1到N中的一个数)，我们可以用下图中的 ρi→k 表示。

随后我们用技巧将它们简化为一个标量，使得算法的时间和空间和输入的相似对的数目成线性相关。
而从函数结点 fk(c) 到变量结点 ci 也包含了N个实值，可以表示为 αi←k(j) .在任意时刻，可以通过将所有的 ci 的输入信息求乘积得到 ci 的评估。

我们先用公式来描述前者，所有的 ρ 信息，也就是从变量到函数结点的信息，都是从变量结点出发的，它们可以所有输入信息逐个相乘：

从函数结点到变量结点可以通过对所有输入信息的乘积，随后summing over掉所有的变量（除去我们发送信息过去的那个变量）。因为所有的函数结点都与N的变量结点相连接，这意味着我们需要对N个函数结点中的每一个求N-1次加法。

O(N3) 向量信息更新

上面的时间复杂度明显是不适用的，所幸的是，所有的函数 {fk(c)Nk=1} 都是二值的约束，所以它们是可以因子分解的：

如果我们对 ck=k 和 ck≠k 进行分开讨论，那么函数就可以写到加法里面去，输入信息就可以单独求加法（也就是说，把求和符号 和 乘号 的位置调换一下）。相应的，我们可以将从函数结点 fk 到变量结点 ci 的信息整理如下：

这个公式一眼看去非常让人头疼，为了容易理解，博主贡献一点个人的啃读领悟，在给定 ci 的情况下，比如说我们i=1, N=5,k=2,那么我们要求的从变量结点2到函数结点1的信息，而变量2其实不仅连接了函数结点1，还有函数结点2 3 4 5 ，要把从这些函数结点到它的信息乘起来。
1. 第一种情况，由于 ck=k=i
所以 fk(j1,...,ji−1,ci,...,jN)≡１ ，所以可得原式第一个分式。
2. 第二种情况，由于 ck≠k=i
根据定义，k不选自己，说明也没有别的数据点选它，只有 j1,j2,...,ji−1,jj+1,...,jN 都不等于ｋ可以使得才能使得 fk 取值为１，否则为０求乘法后就是０这项可以忽略，所以可得原式第二个分式。注意乘法和加法交换了位置。
3. 第三种情况，由于有不是ｋ的数据点选择了ｋ作为代表点，所以应该ｋ必须同时选择本身也作为代表点。所以写当 i′==k ，对应那项因子写成 ρk→k(k)
4. 第四种情况，由于 i≠k 并且 ci≠k ,所以有两种情况，一种是 ck=k ，　把这一项 ρk→k(k) 单独写出来如同第三种情况，当 ck≠k 时，必须要求 j1,j2,...,ji−1,jj+1,...,jN 都不等于ｋ,可以写成第二种情况的形式，只不过这里为了后面的计算方便单独把 ∑j:j≠k ρk→k(j) 　这一项写出来了。

如果我们把这些向量信息看成是相对于 ci 的不变量和变量的乘积，那么问题会变得更加简单，也就是说

ρi→k(ci)=ρ¯i→k⋅ρ˜i′→k(ci)

αi←k(ci)=α¯i←k⋅α˜i←k(ci)

.

因此，我们上面的计算responsibilities的式子变换为：
　　　　　　　　　　　　　　　　
相应的计算availabilities的式子
　　　　　　　　　　　　　　　　　　　　　　　

为了方便，可以设定常量的部分为一个固定值，也就是：
　　　　　　

ρ¯i→k＝∑j:j≠kρi→k(j)

这样一来，变量的部分必须满足：
　　　　　　

∑j:j≠kρ˜i→k(j)=1

　　　　　　　　　　　
因为它们连乘要等于原来的数，而常量部分已经等于原来的数了，所以变量部分必须为１。因此我们又可以进一步得出

∑j=ρ˜i→k(j)=1+ρ˜i→k(k)

　
另外，可以发现，在 αi←k(ci) 中没有表达式直接包含 ci ,而依赖于它的是表达式的选择。
对应的，Ｎ维向量 αi←k(ci) 只有两个不同的值：
一个是 ci=k ，一个是 ci≠k 。

设定 α¯i←k=αi←k(ci:ci≠k) ，这会使得所有的 α˜i←k(ci)=1 ( ci≠k )
（理解这个式子，发出信息的函数结点　不等于　变量的标签）
从而，我们可以推导出在这两种情况下的变化：
（１）对于所有的 ci≠k :

∏k′:k′≠kα˜i←k′(ci)=α˜i←ci(ci)

这个式子容易理解，由于上面的设定，发出信息的函数结点(availability 信息传递是从函数结点到变量结点)的变量部分当 k′≠ci （当然也不等于k）时就会得到１，所以所有不是ｋ也不是 ci 的函数结点发给变量结点i的乘积为１。
换言之，用更通俗的说法就是，发出结点如果和标签值 ci 是不同的，那么其值就是1，发出结点我们确定了不为k, 然而我们并不能肯定它是否为 ci , 因为 k≠ci , 所以，最后只剩下 ci 这个函数结点发出的部分了。

（２）对于 ci=k
需要满足

∏k′:k′≠kα˜i←k′(ci)=1

我们自然可以得出，只用排除一种情况，那就是发出结点 k′ 不为ｋ，由于ｋ和 ci 相同，它自然也不等于函数的标签。因此各项都是１，相乘自然也是１。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

公式的变形

得到上面的结论后，我们对之前的公式可以进一步的简化。

同样对于availabilities的变化。

现在，我们可以将之前的表达式再换一种形式

ρi→k(ci)=ρ¯i→k⋅ρ˜i′→k(ci)

返回来写：

ρ˜i→k(ci=k)=ρi→k(ci=k)ρ¯i→k

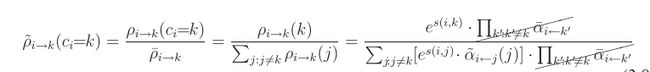
同理，对于 α˜ 也可以重新改写其形式：

从上面式子中可以看出，由于常量的巧妙设置，在 ci=k 的变量部分，其实分别等于对应的上面的公式中第一种情况/第二种情况，　第三种情况/第四种情况。
进一步我们又可以消除其中的常量项。

O(N3)标量信息更新

上面我们最后的计算部分，其实没有包含 ci≠k 的部分，那是因为我们已经计算了。
当 ci≠k 时， ρ˜i→k(ci) 和 α˜i←k(ci) 在实际更新中都没有用到，具体说来，由于 α˜i←k(ci≠k)=1 ,我们其实可以考虑用一个标量来表示信息，而不必要用到一个Ｎ维的矢量。考虑到数值范围的问题，在log domain来工作，我们将从变量结点到函数结点的标量定义为： er(i,k)=ρ˜i→k(k) ,而从函数结点到变量结点的标量定义为: ea(i,k)=α˜i←k(k) 。

代入上一节的公式，我们可以得到。

r(i,k)表示成responsibility,表示从数据点i到候选代表点ｋ，代表着在同时考虑除去ｋ的候选的代表点的evidence的和的情况下，ｋ有多适合作为ｉ的代表点。
a(i,k)表示成availability,综合考虑别的同样认为ｋ适合作为代表点的数据点的信息，ｋ有多适合作为ｉ的代表点。
所有的数据点要不然就是一般的数据点，要不然就是代表点，取决于它们是在发送\接收　availability\responsibility 信息。

在若干轮的迭代后，我们要评估变量 ci 的值，通过将所有输入给变量结点 ci 的信息的乘积，然后求使它最大值的ｊ。

另一种包含了availabilities 和responsibilities但是没有包括输入的相似度做法，可以通过在分子分母乘以一个常量获得，最终结果是不会改变的

O(N2) 标量信息更新

在每一轮迭代中，包含了计算 N2 条availability以及responsibility信息的计算(就是Ｎ个点到Ｎ个点，所以是Ｎ^2),而在公式：

中，每一条信息的更新都需要 O(N) 的计算量，所以整个网络一次迭代的计算量为 O(N3) 。如果我们把表达式中一些中间值定义为：

R(i)=∑k′=1Nes(i,k′)+a(i,k′)

A(k)=∏i′=1N[1+er(i′,k)]

这样之前的公式可以重新写成：


　
而这些累加和累积的运算，我们在迭代的开始可以全部算出，时间复杂度为 O(N2) ,随后的信息更新就可以在 O(1) 的时间完成。这将使得整个算法的时间复杂度为 O(N2)

然而，在实际应用中，这种算法可能会导致数值上的不稳定。这是因为我们在计算 ∑k′≠kes(i,k′)+a(i,k′) 时，用 R(i)−es(i,k)+a(i,k) , 计算机数值的精度有限。为了克服这个问题，我们需要存储和的累积值，同时修改相应的计算 R(k) 和 A(k) 的表达式。

２. Max-Product Affinity Propagation

引入Max-Product 算法，我们可以克服数值精度的问题，同时我们还能使得聚类结果对输入的similarities具有不变性，不会因为加入一个常数项而改变——
什么意思呢？对于sum-product affinity propagation,只有在responsibilities的计算公式中用到了 similarities，在指数的位置加入一个常数项，相当于分子坟墓各乘以一个常数项，对结果没有影响。

er(i,k)=es(i,k)/∑k′：k′≠k[es(i,k′)ea(i,k′)]=es(i,k)+constant/∑k′:k′≠k[es(i,k′)+constantea(i,k′)]

在max-product 中，还增加了一个特点,对乘常数也是具有不变性的。（后文会解释）

相比sum-product的算法，变量结点到函数结点的信息在max-product中是不变的。

ρi→k(ci)=es(i,ci)⋅∏k′:k′≠kαi←k′(ci)

但是，外面的求和符号替换为max运算符。

这４种情况的讨论和上文大同小异，前三个公式都可以直接用max运算符替换求和运算符，所不同的最后一个公式，不再是把两种 ck=k 和 ck≠k 两种情况加起来，而是求它们二者的较大值。为了方便读者阅读，我再把上文的公式，对应的贴一遍：

和sum-product中算法相同，将它们表示成常量和变量的乘积。

ρi→k(ci)=es(i,ci)⋅∏k′:k′≠kα¯i←k′⋅∏k′:k′≠kα˜i←k(ci)

随后设定 ρ¯i→k=maxj:j≠kρi→k(j)
从而得到： maxj:j≠kρ˜i→k(j)=1 .
对于这一步博主的理解是：

ρi→k(ci)=ρ¯i→k⋅ρ˜i′→k(ci)

maxρi→k(ci)=ρ¯i→k⋅maxρ˜i′→k(ci)

所以可得

maxj:j≠kρ˜i→k(j)=1

.

Dueck大牛博士论文这里是有错误的，写成了等于０；

就是说当ｊ不为ｋ时，从变量结点ｉ发送到函数结点k的信息，在标签为ｊ时，它等于０，所以再加上 j=k 的情况就可以综合得到：

maxjρ˜i→k(j)=max[1,ρ˜i→k(k)]

对于availabilities的部分，可以设定 α¯i←k=αi←k(ci:ci≠k) 。这会使得 α˜i←k(ci)=1 对于 ci≠k
和我们上节同样的推理过程，可以得到：
(1) 当 ci≠k 时

∏k′:k′≠kα˜i←k′(ci)=α˜i←ci(ci)

(2) 当 ci=k 时

∏k′:k′≠kα˜i←k′(k)=1

所以可以得到和上文相同的化简形式：

以及：

同样为了方便读者对比，我把sum-product 对应的公式也得出来，可以发现改变的地方是微小的。

再接下来的步骤，想必大家也知道了，我们知道在 ci≠k 时的变量部分，现在要求出在c_i=k ci=k 时的变量部分，而这是一个so easy 的约分的过程，具体推导参考上节。

定义 r(i,k)=logρ˜i→k(k)
a(i,k)=logα˜i←k(k)
第一个公式变成

∀i,k:r(i,k)=s(i,k)−maxk′:k′≠k[s(i,k′)+a(i,k′)]

我们再来看第二个公式，当k=i时

log(∏i′:i′≠imax[1,ρ˜i′→k(k)])=∏i′:i′≠imax[log(1),log(ρ˜i′→k(k))]=∑i′:i′≠imax[0,r(i′,k)]

当 k≠i 时，由于我们存在

logxmax(1,x)=min(0,log x)

所以可以得到：

∀i,k:a(i,k)=min[0,r(k,k)+∑i′:i′∉{i,k}max(0,r(i′,k))]

Affinity propagation算法

我们可以总结，整个算法的流程如下：

---

参考文献：
Affinity propagation: clustering data by passing messages(多伦多大学博士论文)