循环神经网络（Recurrent Neural Network，RNN）

1. 为什么要用循环神经网络

  如下图所示是一个填空系统，他需要做的是给定一句话，然后从这句话中选出需要的词填在对应位置的空中，具体来讲如下图所示

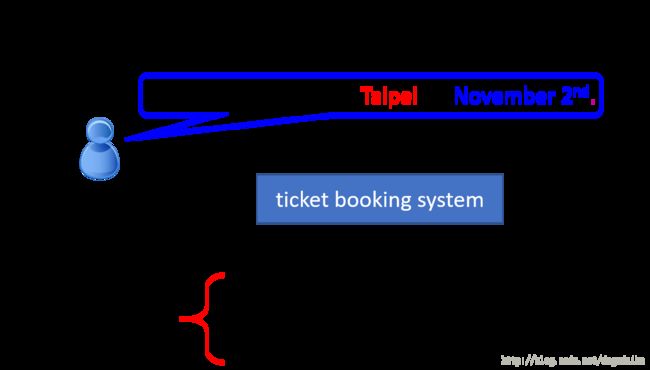
比如说输入一句 “I would like to arrive Taipei on November 2nd.”那么订票系统给就应该自动的在 目的地出填入 Taipei ，在到达时间填入 November 2nd。我们可以使用一个简单的前向传播网络实现这个功能，神经网络的输入可以是单词，输出是这个词是目的地还是出发地。这样样他的输入就应该是单词，以向量形式。获得词向量的方法有很多，比如说最简单的 1-of-N encoding。

  对输入单词的编码也可以采用如下的方式

左侧的这种方法在 1-of-N encoding 的编码过程中加入了其他这一种选项，用这个来表示所有的没有见过的单词。另一种方法是使用字哈希的方法，这样无论出现什么样的单词都可以根据字哈希进行编码表示。

  但是这种方法存在一个问题，就是说对于同样的单词，他没有办法区别它是出发地还是目的地，如下图所示

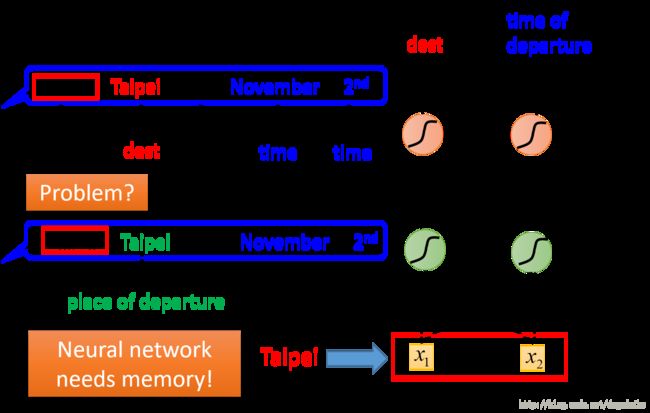
虽然后面的单词都是一样的，但是 arrive 与 leave 完全表示两种不同的意思，但是网络无法记住在 Taipei 前面出现过什么样的单词，也就没有办法判断它到底是出发地还是目的地。但是如果我们的网络存在记忆，就可以很好的解决这个问题。

2. 循环神经网络（Recurrent Neural Network，RNN）

2.1 RNN的简单原理

  RNN 的简单原理如下图所示

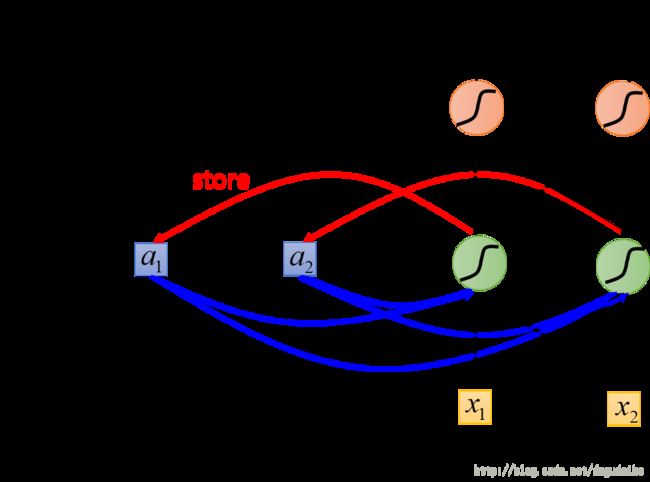
如下是 RNN 的一个原理图，如图所示，他将神经元的输出收集起来并储存，在下一次的时候再输入。

  下面是对这种原理的一种简答的演示

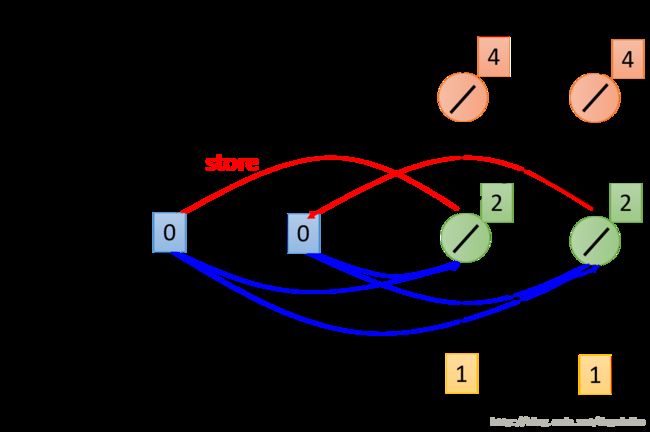
假设神经网络的权重都是1，所有的神经元都是线性神经元，给定记忆单元的初始值为 [0,0]。首先输入向量 [1,1] ，这个时候我们计算第一层神经元的输出是 [2,2]，我们将这个输出的值存贮在记忆单元，计算出此时神经网络的输出为 [4,4]。

  然后输入第二组数据，具体过程如下

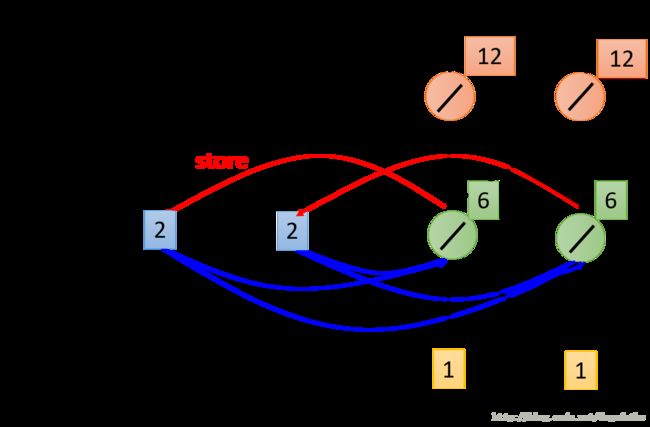
这个时候如果仅仅计算输入的作用的话，第一层神经元的输出值为 [2,2]，但是这个时候因为由于储存单元的存在，还需要加上两个2，所以这个时候第一层神经网络的输出值为 [6,6]，并将这个6放入记忆单元，计算此时的输出为 [12,12]。

  计算最后一组输入数据如下

同样是根据输入数据以及记忆单元的值，计算每一层神经元的输出，最后结果如上图所示。并且在这里值得注意的是，神经网络的输出实际上是和数据的输入顺序相关的，如果调整神经网络的输入顺序，他的输出值就是不同的，这一点恰好说明了RNN似乎有一种记忆力，可以记住之前的输入。

  如下图所示，RNN看起来好像是训练了很多的模型，但实际上并不是，它只是将一个模型使用了多次。

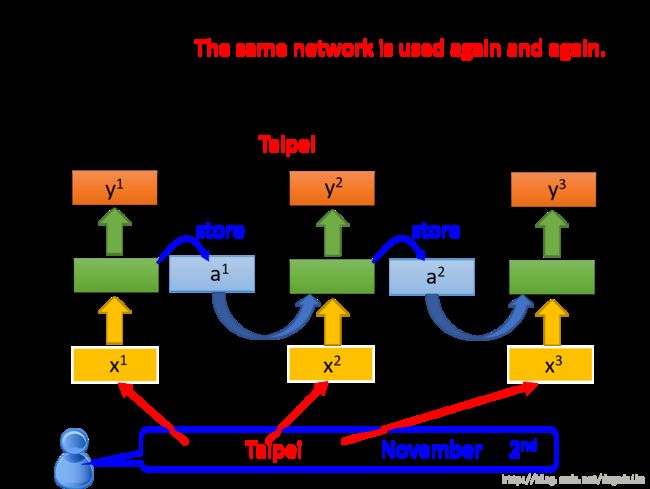
  现在再考虑之前的那个问题，如下图所示

虽然现在我们的输入还是相同的，都是 Taipei 但是这个时候他前面的次是不同的，所以造成记忆单元内的值是不同的，这样 Taipei 也就变得和之前不一样了。

同样 RNN 也存在 deep 的形式，如下图所示叠加了很多的隐层

2.2 RNN 的变形

  当然RNN也存在着以下两种变形

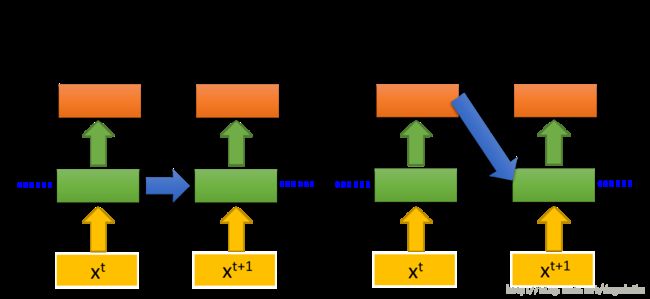
上图中左侧的这种网络称为 Elman Network，它将存下来的值在传递的过程中再乘以相应的系数；另一种网络结构是 Jordan Network ，这种网络结构如上图的右图所示，在这种结构中我们将输出记忆并在下一个数据输入时加入进来，这种网络的有点在于可控。之前的方法，都是将中间层记忆下来，但是这种方法是不可控的，因为中间层是没有办法控制的，但是输出层是有target 的，所以可控性更好。

  双向RNN网络也是一种典型的变形形式，结构如下图所示

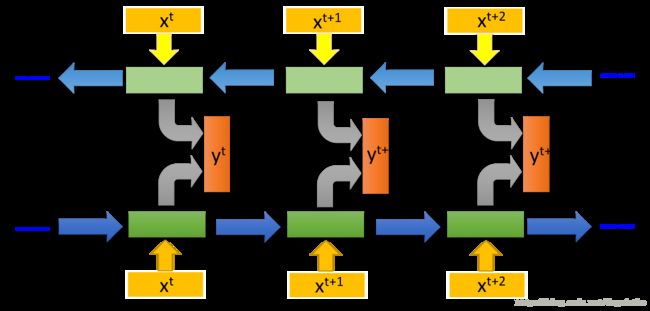
原先的RNN有这样的缺点，对于输入的一个整个句子，他在没有读完整个句子的时候就给出了一个输出，但是如果根绝下个输入恰好可以说明上一个输出是错的话，那么就十分尴尬了。在双向RNN中，句子会正想输入一遍，还会反向输入一遍， 然后将上下两层神经元都放入同一个输出层中，得到最后的输出结果。

2.3 长短时记忆(Long Short-term Memory ，LSTM)

  RNN还有一种很典型的变形就是LSTM，这种形式 RNN 实际上是现在的主流，如果一个人说它使用了RNN，那么实际上他很有可能时使用了LSTM。其中有一个小的细节需要注意，连字符“－”是连接在 short 和 term 之间的，原因在于原来的模型是短时记忆，现在的是比较长的短时记忆。

  对于 LSTM 的说明如下图所示

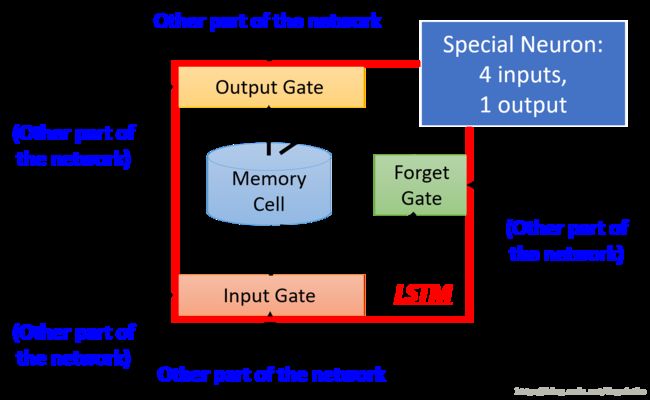
它是一种特殊的神经元，它有4个输入和1个输出，第一个输入就是普通的输入，第二个输入控制输入信号门是否打开的信号，第三个输入是控制遗忘门是否打开的信号，最后一个输入是控制输出门是否打开的信号；而输出就是普通的输出。在这里 Memory Cell 是通过 Forget Gate 和 Input Gate 进行输出的。

  它也可以表示为如下的抽象式的形式

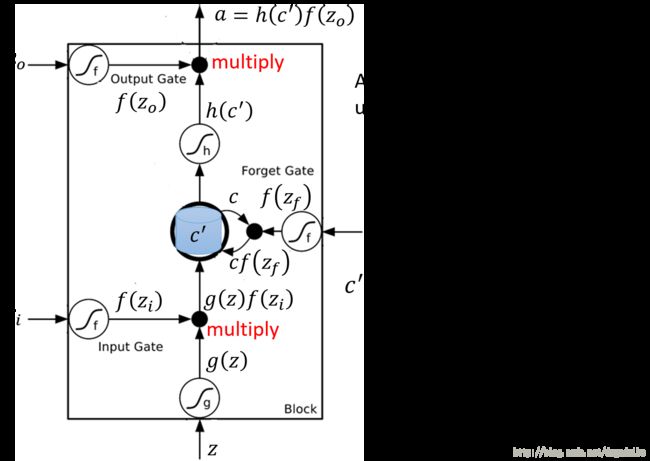
在这里输入信号 z ，经过 sigmoid 神经元获得 g(z) ，输入门控制信号 zi ，经过sigmoid 神经元获得 f(zi) ，将两者相乘获得 g(z)f(zi) ，这里的相乘就可以体现出门信号的控制作用，因为0 的时候就可以控制它不通过，1的时候就可以控制他通过。遗忘门的输入为 zf ，经过sigmoid 神经元获得 f(zf) ，这个时候更新 Memory cell 中的值为 C′=g(z)f(zi)+Cf(zf) ，然后将得到的 C’ 经过sigmoid 神经元获得 h(c′) 。输出门信号 z0 通过sigmoid 神经元获得 f(z0) ，将它们相乘获得输出的值 a=h(c′)f(z0) 。

2.3.1 LSTM 手工计算例子

  手工计算的例子如下

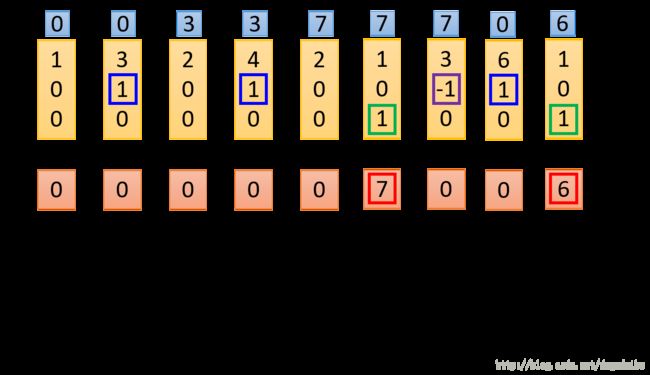
在这里输入是一个三维的向量，输出一个实数值。对于门信号的控制方式如下，其中当 x2=1 的时候，将 x1 的值添加在记忆单元中；当 x2=−1 的时候，将记忆单元中的值清空；当 x3=1 的时候，输出单元中的数值。

  对于第一组输入数据，计算的过程如下图所示

如上图所示，其中黄色的方框是网络的输入，绿色的方框是偏置 b ，对于四个输入信号，它们的权重已经在图中给出了。对于给所给出的这组数据，input 得到的是3，门信号得到的是1，将两者相乘得到的是3。记忆单元中的初始值是0，记忆单元的门信号经过网络的输出是1，更新记忆单元内的值为 c′=3+0∗1=3 。这个值经过线性单元的到3，此时输出门信号为0，所以最后神经元的输出值为0。

  同样可以对第二组数据进行计算，如下图所示

其中需要注意的是记忆单元的计算，在输入上一个数据时，记忆单元内的值为3，此时遗忘门的控制信号为1，所以这个时候遗忘单元的值要进行更新，4+3=7，所以现在看他的值是7。

  剩下三笔数据的更新如下图所示，具体过程省略

2.3.2 循环神经网络 RNN 的简化形式

  正常的前向传播神经网络如下图所示

RNN也可以化简为如上的形式，具体的如下图所示

原先每个神经元相当于接了2个神经元，在这里相当于接了8个神经元。所以使用的参数的数量是原来的4倍。

  为了看出 LSTM 与 RNN 的关系，我们继续将图化简为如下的形式

其中 zi 是输入向量乘以一个权重矩阵的得到的向量，它的每一维都是 input gate 的一个输入，同理我们得到了总共四个向量 zf,zi,z,zo 。

  所以一个单隐层LSTM的形式如下

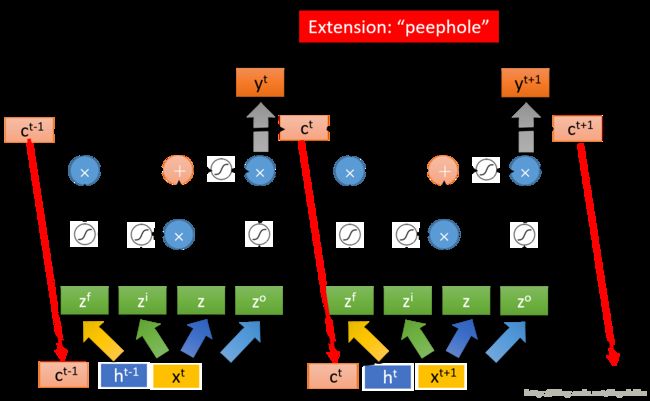
这是LSTM在两个相邻时刻的情况，首先不看输入层的 c 和 h，这里所进行的运算就是之前LSTM所进行的运算。但是这只是一个简化版的LSTM，真正的LSTM的结构是需要添加上面的 c 和 h，它将memory cell 中的值和输出层的值作为输入由返回给了输入层。将 c, h, x 都乘以一个变换矩阵之后，在进行训练。

  当然现在的网络都叠的比较深，多以LSTM也存在deep的形式，如下图所示

这样的网络看起来是十分复杂的，给人的以印象可能是不会work，但是实际上现在这种网络已经成为了RNN的标准，基本上每一个使用RNN的人，他用的基本都是LSTM。

2.4 RNN 的训练

  RNN的训练过程如下图所示

在这个训练过程中，我们的输入是一段句子，他有很多单词，我们将 arrive 标记为 other ，将 Taipei 标记为 dest，将 剩下的都进行了标注，如上图所示。对于 x1 我们的输入是 arrive ，他的输出向量应该是如上图所示的编码，所以损失函数就是实际输出的向量与正确答案之间的交叉熵，之后依次这样训练下去。但是有一点是需要注意的，一定要按照正确的顺序输入，因为RNN的输出与输入的顺序有关。

  训练的过程仍然采用梯度下降法。在之前的前向传播网络中曾经提到过，为了有效地进行梯度下降，我们使用反向传播的方法，同样地在RNN中为了计算梯度方便，也提出了相应的算法，称为　Backpropagation through time (BPTT)

  但是不幸的是，我们并不能总是顺利地训练我们的网络，比如说可能会产生下图所示的情况

有的时候会产生蓝色的那条训练曲线，这时很幸运的；但是有的时候也会会遇到绿色那条线的情况，在一瞬间 loss 变得无穷大使得训练过程就这样终止了。

  提出RNNN的人对这种现象进行了分析，他发现损失函数的曲面是如图所示的

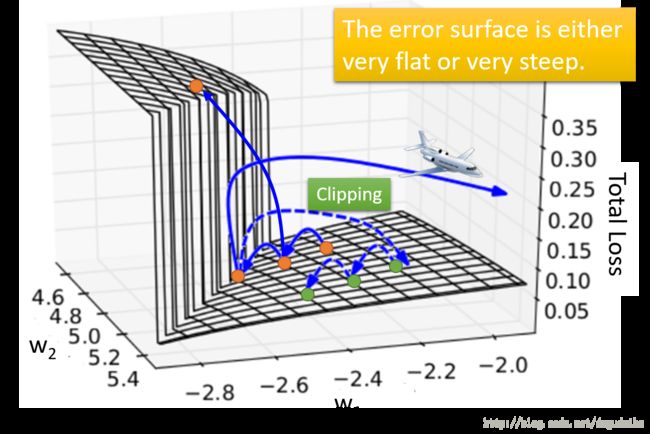
这个误差曲面要么是非常平坦的，要么是非常陡峭的。如橘黄色的点的更更新过程，如果他一不小心调高了悬崖的上面，那么整个损失函数就会突然变大；如果更不小心，直接踩到了悬崖与平原的交界处，这点的梯度是十分大的，会使训练结果直接飞出去。

  那么为什么会产生这样的现象呢？原因主要在于同一个权重被重复使用数次，如下图所示

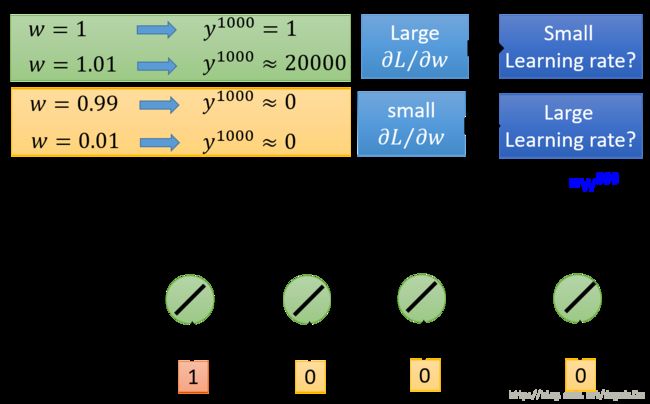
虽然直接通过梯度下降的过程进行分析会比较严密和直接，但是由于形式比较复杂，所以在这里我们考虑 w 一个微小的改变给输出值带来的影响来近似考虑。假如现在有一个十分简单的网络如上图所示，只在第一个时刻的输入为1，其他时候的输入都是0，当权值增加0.01 的时候输出值增加了约20000倍，这个就会造成上述所说的悬崖的产生；当权值减小0.01，达到0.99的时候，此时的输出为0，但是如果我们将权值直接变为 0.01，那么网络的输出同样是0，这个时候就会出现十分平坦的平原。

  解决这个问题的一种技术是，对于梯度的增量给一个限制的值，算出梯度的增量大于这个限制的值的时候，就只能取这个值，用这样的方法可以解决上图中那种类似于梯度爆炸的方法。

  而解决这样的问题的另一种技术就是使用LSTM技术，这种技术的主要目的是取出平坦位置给训练带来的问题，如下图所示

与 RNN 不同，RNN 中的 memory cell 中的值每一次都会被清除，但是在 LSTM 中，一旦这个值对网络产生了影响就会已知存在，除非它通过控制遗忘过程的讯号将自己遗忘了。所以有的人会说，如果想让网络工作的比较好，要尽量少的进行遗忘这部操作；另外一种改进的方式就是GRU，他将 input 与 forget 联动，只有当 input 打开的时候，forget 才会清楚 memory，这样的方法可以减少模型中的参数，抑制模型的过拟合。

  或者也可以采用其他的方法进行改进，如下图所示

比如说使用Clockwise RNN ，或者使用Structurally Constrained Recurrent Network (SCRN)。另外有一种比较有意思的改进是Hitton 提出的，这种方法仅仅使用最普通的 RNN，通过使用单位矩阵初始化和ReLU就可以得到很好的效果，而不是使用LSTM。

3. RNN 的更多应用

3.1 情感分析（Sentiment Analysis）（多对一）

  输入一个句子，输出的对于这句话的情感的分析

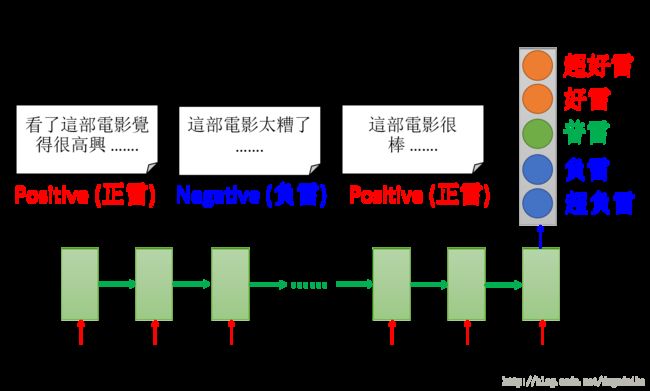
然后把中间的 hidden layer 拿出来，可能后续还需要一些其他的处理转化，得到最后的情感结果。

3.2 提取关键词（多对一）

  给machine 看一些文章，然 machine 自动提取出其中的关键词，如下图所示

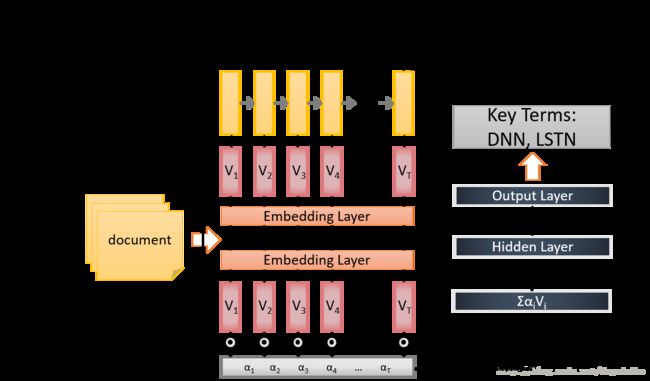
他将文本首先输入 Embedding Layer 之后输入 RNN ，将RNN最后一个时刻的输出接入 attention ，再将结果接入一个DNN，得到最后的结果。

3.3 语音识别（Speech Recognition）（多对多）

  RNN 也可以用于多对多的情况，在这种情况下要求输出的长度小于输入的长度，而语音识别就是这样的一种例子，如下图所示

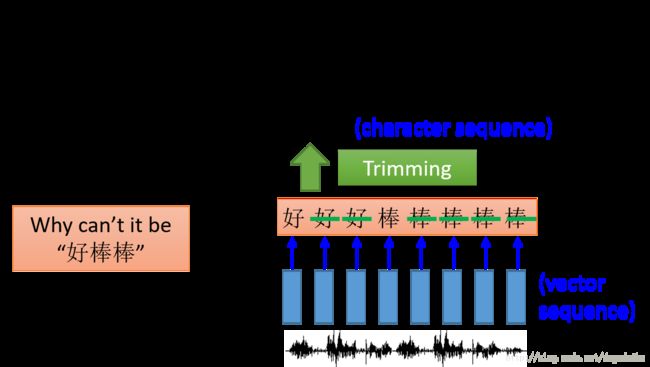
将输入分割成小的向量，之后进行训练。在测试的过程中可能存在很多段这种小的语音对应相同的字的情况，这个时候我们就将重复出现的字去掉，获得最后的结果。但是这样也会出现同样的问题，即无法处理叠词。比如说语音输入为“好棒棒”，但是辨识出的文字是“好棒”，这个时候语音辨识出的结果就与实际的含义完全相反（在台语中，好棒棒与好棒恰好是反义词，实际上在普通话中也有这种含义在其中）。这样我们就需识别叠词的方法，具体如下

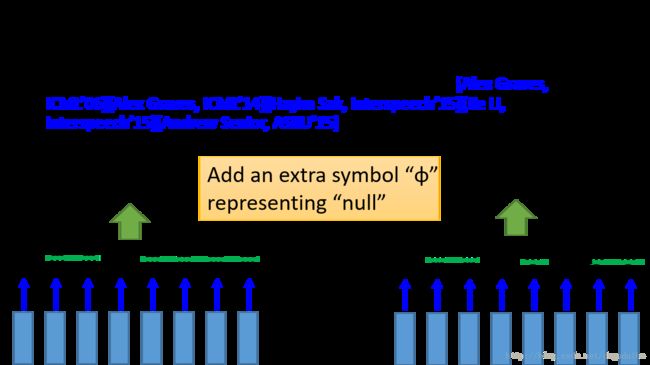
  在这将空的输出用 ϕ 表示，这样就可以区别出好棒与好棒棒，这一种方法的名字交CTC。那这种方法是如何进行训练的呢？如下图所示

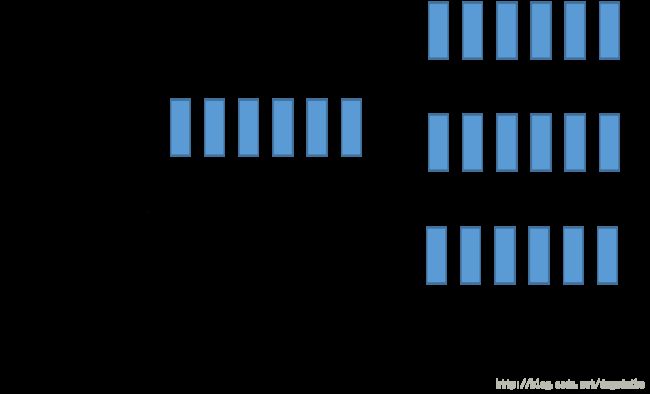
我们现在只是知道这样的一段语音，他对应着好棒，但是我们并不知道具体是哪一个小部分对应着棒，哪一个部分对应着 null，所以就穷举所有的可能，将它们一同输入进行训练，这样的看起来是很麻烦的，但是实际上有着一个巧妙的演算法。

  这种方法的一个具体如下所示

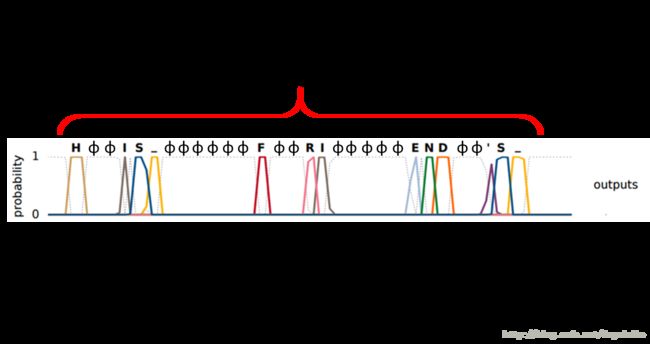
他输入一段语音，输出是字母，如果单词之间存在着空白的部分用下划线表示，如上图为输出的结果。传说中，目前谷歌的语音辨识系统已经全面换成了这种CTC的形式。

3.4 机器翻译（Machine Translation ）（多对多）

  在上面的例子中，要求输出的向量的长度要小于输入向量的长度，但是在机器翻译中对长度是没有要求的，如下图所示

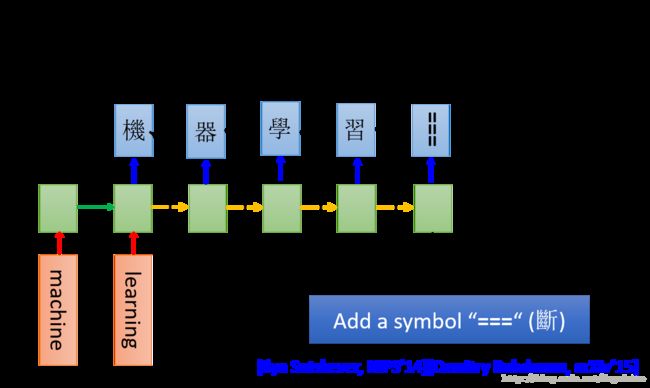
我们将整个句子输入RNN，这个时候最后一刻的输出就已经看完了整个句子，假设这个时候输出的是“机”，然后将“机”作为下一时刻的输入，再产生“器”，就这样一直执行下去，理论上他会一直执行下去，并不知道应该在什么时间停止，所以这个时候我们就应该在输出中增加一种可能是“===”，代表断，即停止的意思。

  另一种做机器翻译的方法是直接将语音输出，然后直接输出翻译的文字，而不需要先进行语音辨识再进行翻译，具体的例子如下

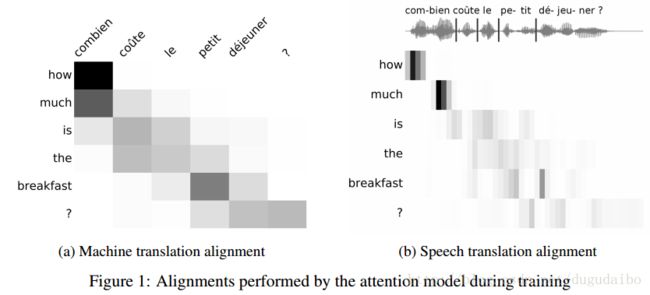
这种方法的好处在于对于某一种文字不是很完备的语种，可以直接收集语音并进行翻译，在搜集数据的时候比较方便。

3.5句法分析（Syntactic parsing）

  使用RNN同样可以实现句法分析，具体方法如下

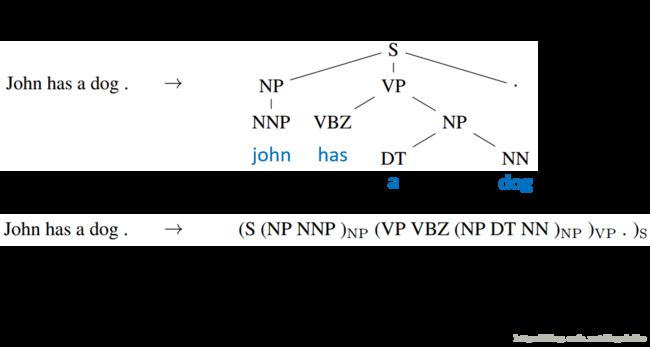
我们将一句话额句法树表示为如下的向量形式，直接利用RNN进行训练，可以完成句子的句法分析。

3.6 文本自编码

  如果我们使用 bag of word 的方法，往往没有办法得到句子的含义，如下图所示

这两个句子的 bag of word 是完全相同的，却有着完全相反的意思，为了解决这中问题需要提取出句子的语义，便采用了如下的文本自编码的方法

这样 encode 中就包含了句子中的重要含义，也就可以很好的区别上面这两个句子了。

  他也可以使用如下这种分层的网络结构

在这种网络中他首先将单词变成 encode word ，然后转成句子的编码，最后再一路解码回去。

3.7语音自编码器

  我们也可以类似地将语音进行自编码，编码得到的向量可以用于检索，如下图所示

通过计算两个编码之间的相似程度进行检索。