PAC与样本复杂度

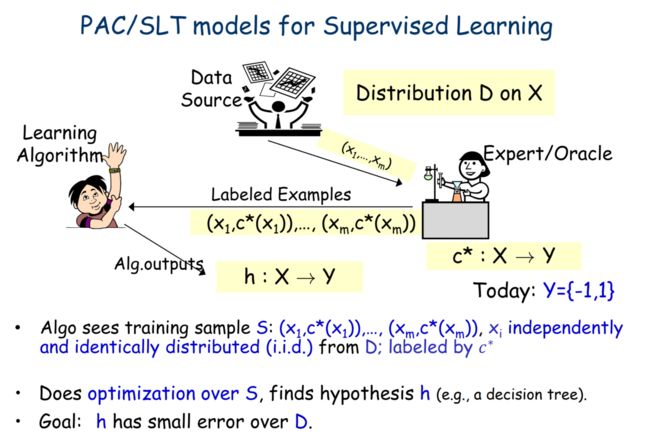
这篇文章主要总结 PAC 学习框架以及样本复杂度相关的东西，大致来说就是:要保证以概率 $1-\delta$ 使得 generalized error 小于 $ϵ$ 需要多大的样本复杂度，以及时间复杂度才是好的。

问题及约定

符号约定

两个 error 符号

就是我们常说的 train error 与 true error

接下来是定义我们要研究的问题

简单的来说就是 依赖于 $m,H,ϵ,\delta$ 这四个东西，我们找到一个 样本复杂度以及计算复杂度的界.或者说找到他们的一些关系

定义

consistent hypothesis:

$consistent(h,S)|=h(x)=c(x),\forall (x,c(x))\in S$

一个 假设称为是 consistent 的，if and only if, $\forall (x,c(x))\in S$ 都有，$h(x)=c(x)$

Version Space:

$V{S}_{H,S}:\{h\in H|consistent(h,S)\}$

$ϵ-exhausted$

$V{S}_{H,S}$ 称为 $ϵ-exhausted$,当且仅当,

$\forall h\in H,erro{r}_D(h)<ϵ$

throme

这个定理的证明会在文末给出，接下来的核心就在于理解这个定理

理解

这个定理的前提:

1. $Hfinite$
2. $c\in H$

注意这个定理说的是 not，将这个定理翻译一下就是

$\mathrm{Pr}(\exists h\in H,(erro{r}_S(h)=0)\&(erro{r}_D(h)>ϵ))<|H|{\exp }^{-ϵm}$

也就是说 如果 $erro{r}_S(h)=0$, 那么 $erro{r}_D(h)<ϵ$ 的概率至少是 $|H|{\exp }^{-ϵm}$

如果我们想要让 $|H|{\exp }^{-ϵm}<\delta$, 那么我们需要

$m>{ϵ}^{-1}(\log (|H|)+\log ({\delta }^{-1}))$,这么多变量

if $erro{r}_S(h)=0$ 那么 至少我们有 $1-\delta$ 的概率保证

$erro{r}_D(h)\le m^{-1}(\log (|H|)+\log ({\delta }^{-1}))$

PAC learnable

简单的说，一个算法是 PAC(Probability Approximation Correct) 可学习的，要满足，时间复杂度和样本复杂度都是多项式的

agnostic learning

上面都说的是 $c\in H$ ，那如果， $c\notin H$ 呢？

根据 Hoeffding 不等式(see wiki)

fix a $h$,

$\mathrm{Pr}(erro{r}_D(h)-erro{r}_S(h)>ϵ)\le 2{\exp }^{-2m{ϵ}^2}$

修改前面的定理，

$\mathrm{Pr}(\exists h\in H,erro{r}_D(h)-erro{r}_S(h)>ϵ)<|H|2{\exp }^{-2m{ϵ}^2}$

因此在概率为 $\delta$ 的情况下，需要的样本 bound

就可以很容易求解了

erm

最后不加证明的给出

即 如果我们知道 $er{r}_S(h)$ 那么 $erro{r}_D(h)$ 的bound 在哪里?
所有的证明和材料，都可见reference

reference

1. 10716 f16 Eric Xing
2. 10715 f18 Maria-Florina Balcan

版权声明

本作品为作者原创文章，采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议

作者: taotao

转载请保留此版权声明，并注明出处