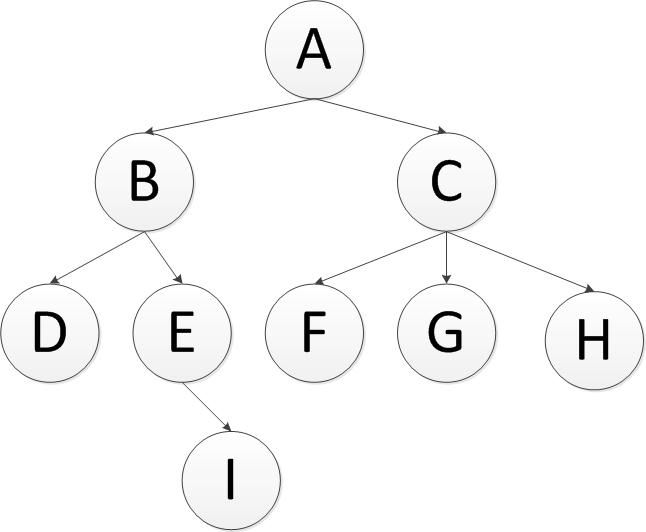
在编程生活中,我们总会遇见属性结构,这几天刚好需要对树形结构操作,就记录下自己的操作方式以及过程。现在假设有一颗这样树,(是不是二叉树都没关系,原理都是一样的)
1、深度优先
英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。对于上面的例子来说深度优先遍历的结果就是:A,B,D,E,I,C,F,G,H.(假设先走子节点的的左侧)。
深度优先遍历各个节点,需要使用到堆(Stack)这种数据结构。stack的特点是是先进后出。整个遍历过程如下:
首先将A节点压入堆中,stack(A);
将A节点弹出,同时将A的子节点C,B压入堆中,此时B在堆的顶部,stack(B,C);
将B节点弹出,同时将B的子节点E,D压入堆中,此时D在堆的顶部,stack(D,E,C);
将D节点弹出,没有子节点压入,此时E在堆的顶部,stack(E,C);
将E节点弹出,同时将E的子节点I压入,stack(I,C);
...依次往下,最终遍历完成,Java代码大概如下:
public void depthFirst() {
Stack> nodeStack = new Stack>();
Map node = new HashMap();
nodeStack.add(node);
while (!nodeStack.isEmpty()) {
node = nodeStack.pop();
System.out.println(node);
//获得节点的子节点,对于二叉树就是获得节点的左子结点和右子节点
List> children = getChildren(node);
if (children != null && !children.isEmpty()) {
for (Map child : children) {
nodeStack.push(child);
}
}
}
}
//节点使用Map存放 2、广度优先
英文缩写为BFS即Breadth FirstSearch。其过程检验来说是对每一层节点依次访问,访问完一层进入下一层,而且每个节点只能访问一次。对于上面的例子来说,广度优先遍历的结果是:A,B,C,D,E,F,G,H,I(假设每层节点从左到右访问)。
广度优先遍历各个节点,需要使用到队列(Queue)这种数据结构,queue的特点是先进先出,其实也可以使用双端队列,区别就是双端队列首位都可以插入和弹出节点。整个遍历过程如下:
首先将A节点插入队列中,queue(A);
将A节点弹出,同时将A的子节点B,C插入队列中,此时B在队列首,C在队列尾部,queue(B,C);
将B节点弹出,同时将B的子节点D,E插入队列中,此时C在队列首,E在队列尾部,queue(C,D,E);
将C节点弹出,同时将C的子节点F,G,H插入队列中,此时D在队列首,H在队列尾部,queue(D,E,F,G,H);
将D节点弹出,D没有子节点,此时E在队列首,H在队列尾部,queue(E,F,G,H);
...依次往下,最终遍历完成,Java代码大概如下:
public void breadthFirst() {
Deque> nodeDeque = new ArrayDeque>();
Map node = new HashMap();
nodeDeque.add(node);
while (!nodeDeque.isEmpty()) {
node = nodeDeque.peekFirst();
System.out.println(node);
//获得节点的子节点,对于二叉树就是获得节点的左子结点和右子节点
List> children = getChildren(node);
if (children != null && !children.isEmpty()) {
for (Map child : children) {
nodeDeque.add(child);
}
}
}
}
//这里使用的是双端队列,和使用queue是一样的