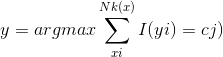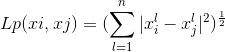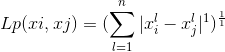机器学习常用算法总结(一)
最近一直在学习机器学习的算法知识,由于是转专业的找着方面的工作的,所以决定通过写博客自己总结常用的算法来加强自己的理解。在这里我会总结常用机器学习算法的原理,公式,参数调优,优点以及缺点。尽量用比较通俗的语言来理解这些知识点,以便记忆
- k-近邻算法(KNN K-Nearest neighbor)
其中x是特征向量,y是实例的类别
输出: 实例x所属的类别y
(1). 根据给定的距离度量方法,在训练集T中找出与x最邻近的k个点,涵盖这个k个点的领域记做Nk(x);
(2). 在Nk(x)中根据分类决策规则(比如多数表决)决定x的类别y:
其中I为指示函数,即当yi = cj时,I为1否则为0.
knn模型有三个基本要素:距离度量,k值的选择和分类决策规则
(1) 距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映。一般使用的是欧式距离来度量两个点的距离但是也有其他的方法
Lp距离定义为:
其中p>=1,当p=2的时候,这个公式表示的就是欧式距离,即:
p=1的时候表示的是曼哈顿距离即
(2) k值的选择
k值的选择会对knn算法的结果产生很大的影响。
简单的总结是k值小是整体模型变复杂,预测结果会对近邻的实例点非常敏感,容易发生过拟合。
如果k值过大模型太简单容易发生欠拟合。在实际应用中
k值一般都会选择一个较小的数值,通常采用交叉验证的方法来选取最优的k值。
通常采用错误率来测试算法优劣
(3)分类决策规则一般都采用多数表决规则,其等价于经验风险最小化
knn算法的优缺点:
优点:精度高,对异常值不敏感,无数据输入的假定
缺点: 计算复杂度高,空间复杂度高
knn的实现方法
knn最简单的实现方法是线性扫描(liner scan)。 这时需要计算每个点与实例点的距离,当训练集很大的时候,
计算非常耗时。kd树是针对这种情况的
另一种实现knn的方法
构造方法如下:
输入:
数据集T={x1,x2, x3...xN},其中每个数据x是k维的
输出:kd树
(1)开始:构造根节点,根节点对应于包含T的k维空间的超矩形区域。
选择x(1)为坐标轴(此处的1表示的是第一维),以T中所有实例的x(1)坐标的中位数为切分点,
将根节点对应的超矩形区域分为两个区域。切分由通过切分点并与 x(1)垂直的超平面实现。由根节点生成的深度为1的
左右子节点。左子节点对应于坐标x(1)小于切分点的子区域,相反右节点对应于坐标x(1)大于切分点的子区域(
此处
的思想有点类似二叉搜索树BST)。将落在切分超平面的实例点放在根节点上。
(2) 重复: 深度为j的节点,选择x(j)为切分轴,l=j(mod k)+ 1。以
x(j)的所有实例的中位数
为切分点,生成超平面分成j+1的左右两个子区域,左边的都
小于切分点,右边区域都大于切分点。切分点落在超平面的实例放在根节点上。
(3) 直到两个子区域没有实例时停止,从而形成kd树
有了kd树,如何实现对实例x的分类呢,这里给出kd搜索树实现最近邻分类
输入:kd树,目标x
输出:x的最近邻
(1) 在kd树中找出目标点x的叶子节点:从根出发,递归向下访问,如果x的当前维的坐标小
于切分点,则移动到左边节点,否则到右边。直到子节点为叶子停止
(2) 在全局中记录此节点为“最近邻节点”,递归的向上回退,在每个节点进行:
(a) 如果该节点与实例的距离小于全局变量“最近邻节点”,则更新
“最近邻节点”为当前节点
(b) 检查当前节点的兄弟节点一下的区域有没有可能有更近的点。具体的以当前节点与目标
点的距离为半径,构建超球体,如果球体与兄弟区域相交
则,另一区域有更近的点,移动到另一个子节点,接着递归进行最近邻搜索。如果不相交,向上回退
(3)当回退到根节点的时候,搜索结束,当前“最近邻节点”就是x的最近邻。
注意到kd树更适合训练实例数远大于维树的knn。(因为O(logn)约等于O(n),当n与维度接近的时候)