数字图像处理--锐化处理
图像边缘锐化基本方法
锐化处理可以用空间微分来完成。
- 微分运算
- 梯度锐化
- 边缘检测
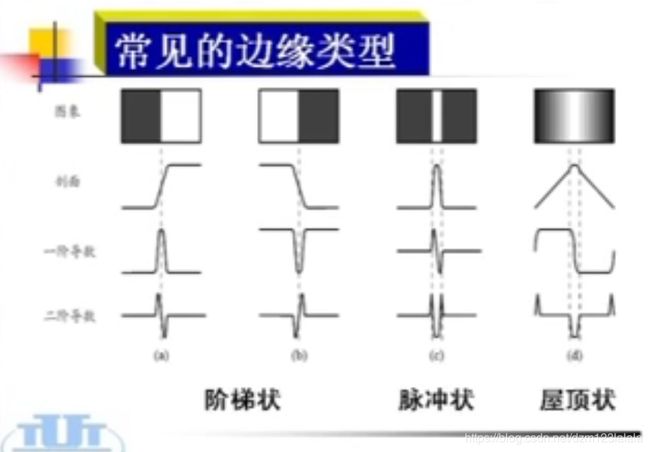
通常,边缘上的灰度值变化平缓,而边缘两侧灰度值变化较快,图像的边缘一般指在局部不连续的图像特征,一般是局部亮度变化最显著的部分,灰度值的变化,颜色分量的突变,纹理结构的突变都可以构成边缘信息。
用差分定义一元函数f(x)的一阶微分:
∂ f ∂ x = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x} =f(x+1)-f(x) ∂x∂f=f(x+1)−f(x)
用差分定义一元函数f(x)的二阶微分:
∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^2 f}{\partial x^2} =f(x+1)+f(x-1)-2f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)
如果被运算点在边缘内部,差分值为很低的值,若是在边缘,则为很高的值。
双向一次微分运算
对灰度图像f在纵方向和横方向两个方向进行违反。改算法同时增强水平和垂直方向的边缘。
计算方法:纵方向求差分,横方向求差分,然后求平方和然后开方
梯度运算
▽ t = [ G x G y ] = [ ∂ f ∂ x ∂ f ∂ y ] \bigtriangledown t=\begin{bmatrix} G_x \\ G_y \\ \end{bmatrix}=\begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \\ \end{bmatrix} ▽t=[GxGy]=[∂x∂f∂y∂f]
▽ f ≈ ∣ G x ∣ + ∣ G y ∣ \bigtriangledown f \approx |G_x|+|G_y| ▽f≈∣Gx∣+∣Gy∣
▽ f = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 \bigtriangledown f=\sqrt{(\frac{\partial f}{\partial x})^2+(\frac{\partial f}{\partial y})^2} ▽f=(∂x∂f)2+(∂y∂f)2
上面这两个公式近似等效
∣ ▽ f ( ∞ ) ∣ = m a x { ∣ ∂ f ∂ x ∣ , ∣ ∂ f ∂ y ∣ } |\bigtriangledown f_(\infty_) |=max \lbrace |\frac{\partial f}{\partial x}|,|\frac{\partial f}{\partial y}| \rbrace ∣▽f(∞)∣=max{∣∂x∂f∣,∣∂y∂f∣}
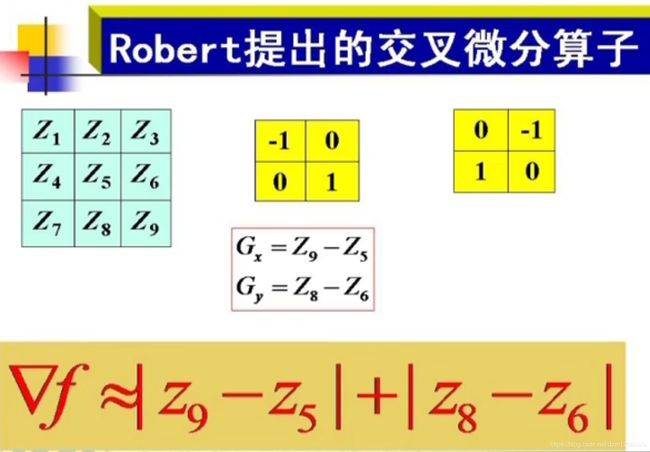
Robert提出的交叉微分算子
Sobel算子
Sobel算子既有平滑作用又有差分作用
Prewitt算子
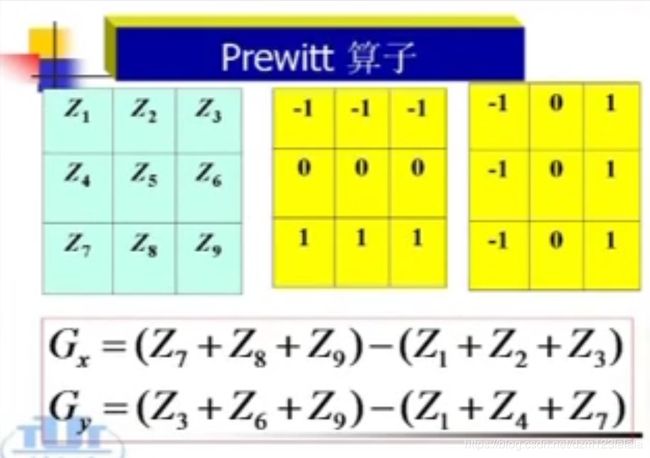
sobel算子和Prewitt算子的区别在于系数,这些求梯度的运算可以利用卷积模板实现。
梯度锐化模板
二阶微分 --拉普拉斯算子
二元图像函数f(x,y)的拉普拉斯变换:
▽ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \bigtriangledown^2 f = \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} ▽2f=∂x2∂2f+∂y2∂2f
x方向:
∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^2 f}{\partial x^2}=f(x+1)+f(x-1)-2f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)
y方向:
∂ 2 f ∂ y 2 = f ( y + 1 ) + f ( y − 1 ) − 2 f ( y ) \frac{\partial^2 f}{\partial y^2}=f(y+1)+f(y-1)-2f(y) ∂y2∂2f=f(y+1)+f(y−1)−2f(y)
由以上两个分量相加,
▽ 2 f = [ f ( x + 1 , y ) + f ( x − 1. y ) + f ( x , y + 1 ) + f ( x , y − 1 ) ] − 4 f ( x , y ) \bigtriangledown^2 f=[f(x+1,y)+f(x-1.y)+f(x,y+1)+f(x,y-1)]-4f(x,y) ▽2f=[f(x+1,y)+f(x−1.y)+f(x,y+1)+f(x,y−1)]−4f(x,y)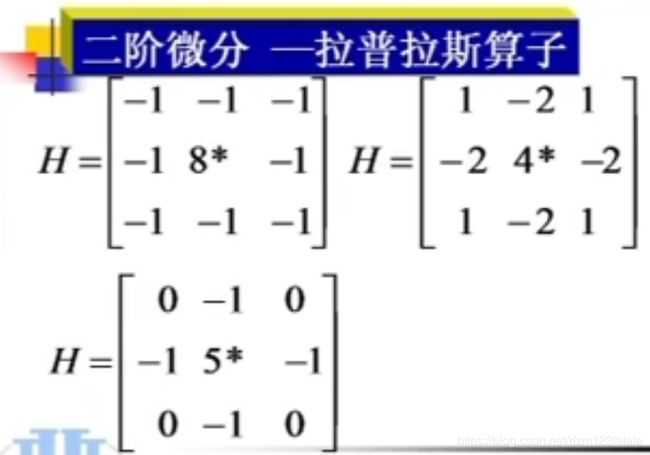
拉普拉斯算子特点:
强调突变,弱化慢变,产生一幅把浅灰色边线,突变点叠加到暗背景中的图像。
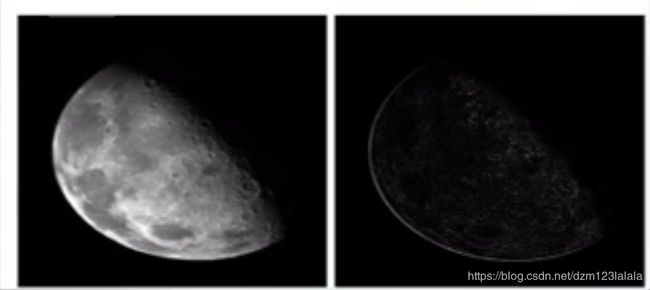
卷积核中心为5的原因:将原始图像和拉普拉斯算子的图像叠加到了一起,原图像为1,Laplace为4,加起来就是5
这样做的好处:既能保持瑞华处理的效果,又能复原背景信息。
高斯-拉普拉斯(log)算子
高斯-拉普拉斯算子是效果更好的边缘检测其,把高斯平滑器是效果更好的边缘检测器,把高斯平滑器和拉普拉斯锐化结合起来,先平滑去掉噪声,再进行边缘检测。
[ − 2 − 4 − 4 − 4 − 2 − 4 0 8 0 − 4 − 4 8 2 4 ∗ 8 − 4 − 4 0 8 0 − 4 − 2 − 4 − 4 − 4 − 2 ] \begin{bmatrix} -2 & -4 & -4 & -4 & -2 \\ -4 & 0& 8& 0& -4 \\ -4 & 8& 24^*& 8& -4 \\ -4 & 0& 8& 0& -4 \\ -2 & -4 & -4 & -4 & -2 \\ \end{bmatrix} ⎣⎢⎢⎢⎢⎡−2−4−4−4−2−4080−4−4824∗8−4−4080−4−2−4−4−4−2⎦⎥⎥⎥⎥⎤
高频提升滤波器
微分运算可以用来求信号的变化率,具有加强高频分量的作用,微分处理厚度图像非常暗,不适用。
如果纪要i去图像的轮廓清晰,又要求保持目标物体的内部灰度不变,这就是高频提升滤波器的目的。
微分运算会使低频成分损失很多,而高频成分突出,为了使得图像边缘清晰,内容完整保留,采用下式:
g ( x , y ) = α f ( x , y ) ± ▽ f ( x , y ) g(x,y)=\alpha f(x,y) \pm \bigtriangledown f(x,y) g(x,y)=αf(x,y)±▽f(x,y)
高斯-拉普拉斯(log)算子就是高频提升滤波器的一种。

自适应检测
采用多个边缘检测算子,不同的检测算子采用不同的方向,不同的邻域导数,用求卷积的方法,计算每个模板,求最大值。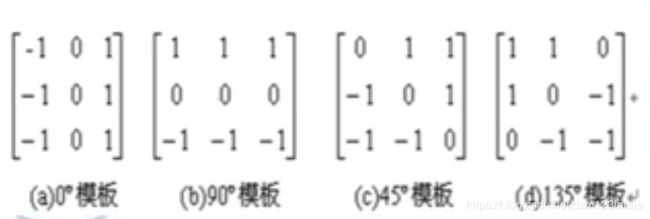
Kirsch边缘检测算子
锐化算子小结
- 好的检测结果:对边缘检测的错误率要低,在检测真实边缘的同时 ,避免检测出虚假的边缘。
- 好的边缘定位精度:标记的边缘位置要和图像上真正的边缘位置尽量接近;
- 对同一边缘要有低的响应次数:有的算子会对一个边缘产生多个相应,本来只有一共边缘点,可是检测出来会出现多个边缘点。要克服噪声的影响。
Roberts算子
利用局部差分算子寻找边缘,边缘定位精度较高,但容易丢失一部分边缘,同时由于图像没有经过平滑处理,因此不具备抑制噪声能力。对陡峭边缘且含噪声较少的有效。
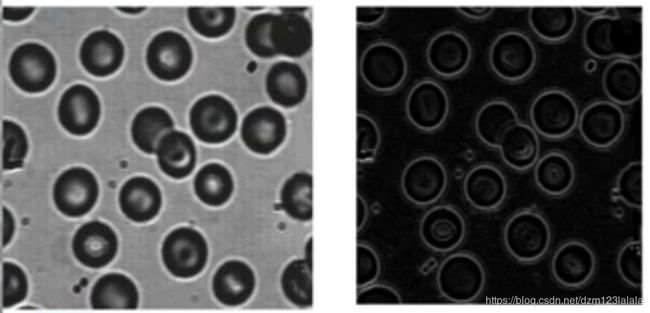
Sobel算子和Prewitt算子
先做加权平滑处理,再做微分运算。平滑部分的权值有些差异,对噪声又一定的抑制能力。但不能完全排除虚假边缘。虽然两个算子定位效果不错,但检测出的边缘容易出现多像素宽度。

Laplacian算子
不依赖于边缘方向的二阶微分算子,对阶跃型边缘定位准确,对噪声非常敏感,使噪声加强,噪声能力差,容易丢失一部分边缘方向信息,造成一些不连续的检测边缘。
LOG算子
先用高斯函数平滑滤波,后用Laplacian算子检测边缘,克服了Laplacian算子抗噪声差的缺点,同时页平滑掉比较尖锐的边缘,尖锐边缘无法被检测到。