《机器学习基石》2-Learning to Answer Yes/No

这节课主要介绍感知器算法（Perceptron Learning Algorithm）。

Perceptron Hypothesis Set

对于一个线性可分的二分类问题，我们可以采用感知器 （Perceptron）这种假设集。

采用这种假设集进行分类的思想是这样的：
我们假设样本的类别是由样本每一个特征 xi x i 共同决定，其中不同的特征的重要程度不一样。于是我们通过对所有的特征进行加权 ∑di=1wixi ∑ i = 1 d w i x i ，得到一个“分数”，将这个“分数”与一个阈值 threshold t h r e s h o l d 进行比较，如果“分数”大于阈值，那么这个样本属于一个类别（类别“+1”），如果“分数”小于阈值，那么这个样本属于另一个类别（类别“-1”）。

这种模型可以用下面的表达式表示出来：

h(x)=sign((∑i=1dwixi)−threshold)    h∈H=sign((∑i=1dwixi)+(−threshold)⋅(+1))=sign(∑i=0dwixi)=sign(wTx) h ( x ) = s i g n ( ( ∑ i = 1 d w i x i ) − t h r e s h o l d )         h ∈ H = s i g n ( ( ∑ i = 1 d w i x i ) + ( − t h r e s h o l d ) ⋅ ( + 1 ) ) = s i g n ( ∑ i = 0 d w i x i ) = s i g n ( w T x )

其中不同的向量 w w 代表了不同的假设函数 h(x) h ( x ) ，我们的目标是使用一些算法调整 w w 的值，使得假设函数 h(x) h ( x ) 与我们要预测的函数 f(x) f ( x ) 尽可能的接近。

我们的想法是：如果 h(x) h ( x ) 与 f(x) f ( x ) 足够接近，那么它们作用在训练集 D D 上的结果会是一样的，即对训练集中的 x x ，有 f(x)=h(x) f ( x ) = h ( x ) 。反过来说，如果对所有训练集中的 x x ，有 f(x)=h(x) f ( x ) = h ( x ) ，那么在一定程度上，我们可以认为 h(x) h ( x ) 与 f(x) f ( x ) 是接近的。

Perceptron Learning Algorithm (PLA)

这个模型中训练 w w 的算法称为感知器算法（Perceptron Learning Algorithm），算法的思想是（尽可能地）对预测错误的样本进行修正，使得分类器的预测结果越来越好。预测错误的样本可以分为以下两种类型：

当 f(x)=y=+1 f ( x ) = y = + 1 而预测结果 h(x)=sign(wTx)=−1 h ( x ) = s i g n ( w T x ) = − 1 时，说明此时 w w 与 x x 的内积过小，夹角过大，需要让 w w 靠近 x x ，因此将 w w 改为 w+x=w+yx w + x = w + y x ;

当 f(x)=y=−1 f ( x ) = y = − 1 而预测结果 h(x)=sign(wTx)=+1 h ( x ) = s i g n ( w T x ) = + 1 时，说明此时 w w 与 x x 的内积过大，夹角过小，需要让 w w 远离 x x ，因此将 w w 改为 w−x=w+yx w − x = w + y x ;

反复修正预测错误的样本点直到所有训练样本都预测正确，选择预测错误的样本的顺序没有限制，可以按自然顺序，也可以随机选择。

算法描述如下图：

A Example

我们举一个例子来说明 PLA 算法的过程。

Guarantee of PLA

目前我们还有一些问题没有讨论，其中比较重要的一个问题是，PLA是不是收敛的，即算法最终能不能停止下来。

首先我们讨论线性可分的情况，线性不可分的情况在下一节中讨论。当数据集是线性可分时，表示存在 wf w f 使得 yn=sign(wTfxn) y n = s i g n ( w f T x n ) ，下面证明PLA是收敛的，即 w w 能收敛到 wf w f ，即算法能停止下来。

1. wf w f 与 wt w t 的内积会单调递增
   
2. wt w t 的长度有限制
   

以上两点可以推出：

当算法从 w0=0 w 0 = 0 开始时，算法更新次数 T≤R2ρ2 T ≤ R 2 ρ 2
其中

R2=maxn{f(x)} R 2 = max n { f ( x ) }

ρ=minnynwTf||wTf||xn ρ = min n y n w f T | | w f T | | x n

因此说明了算法最终会收敛。

Conclusion

我们对PLA进行一下总结：（先用一张图说明，后面再用文字说明）

Convergence

在数据是线性可分的条件下，算法能收敛。

Pros and Cons

• 算法的优点
  算法容易简单、实现；
  算法速度快；
  在任意维度下都能工作。

• 算法的缺点
  需要数据是线性可分的条件；
  不知道算法什么时候收敛。

Non-Separable Data

当数据集是线性不可分时，表示数据中有噪声（这里的噪声是相对于感知器这个假设集而言的）。在这种情况下，学习的过程发生了一点改变：

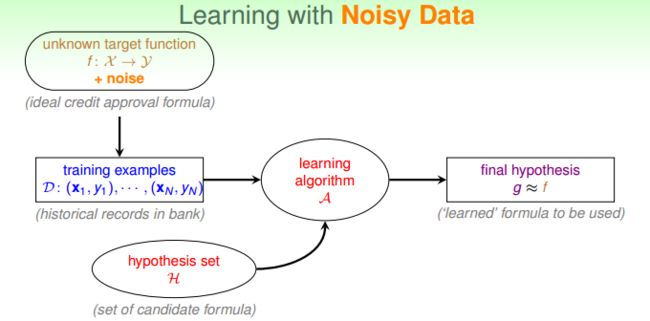
对感知器模型来说，此时可能无法使所有样本都正确分类，此时我们应该退而求其次，找尽可能犯错少的分界面，我们的学习的目标从

argwyn=sign(wTxn) arg w ⁡ y n = s i g n ( w T x n )

变成了

argminw∑[[yn≠sign(wTxn)]] arg ⁡ min w ∑ [ [ y n ≠ s i g n ( w T x n ) ] ]

不幸的是，这是一个 NP-hard 问题。

此时的一种思路是使用贪心算法，于是PLA可以改进成Pocket算法：