【算法专题】数论专题：组合数学

引入

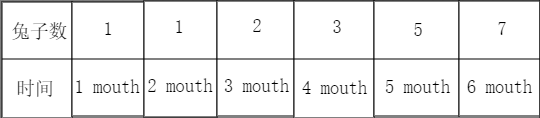
列题：兔子问题
这道题可以怎么写呢？这里有两种方法：找规律&&数学归纳法

找规律

找规律来讲就是递归:

#include
using namespace std;
int main()
{
	int f0=1,f1=1,f2;
	int n;
	cin>>n;
	if (n==1)
    { cout<<"1"<

数学归纳法

找规律在数据量大的情况下，很容易超时，此时，我们必须换一种方法.我们还是以兔子问题举例，找更优的方法。

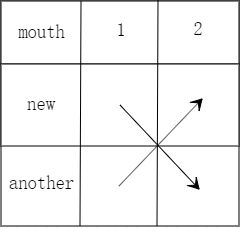
于是，我们就重新合成了一段代码：

f[i]=a[i-1]+b[i-1]+c[i-1]+b[i-1]+a[i-1];

然后，问们进一步简化这个代码：

f[i]=f[i-1]+f[i-2];

把多个算式简化成一种数量关系，这就是数学归纳法.

---

组合数学

基本计数原理

• 加法计数
  做一个事有n类办法，第i类办法有fi种方法，总的方法数为：f1+f2+f3+…fn

经典列题比如说有兔子问题，骨牌铺法。

• 乘法原理
  做一个事分成n个步骤，第i步有fi种方法，那么完成这件事共有f1f2f3*…fn种

经典列题

数的划分I
数的划分II
错排问题
出栈序列问题
括号序列问题
二叉树计数

解析列题（节选）

• 错排问题

n个有序的元素应有n！种不同的排列。如果一个排列使得所有的元素都不在原来的位置上，则称这个排列为错排。任给一个n，求出1，2，3，。。。，n的错排个数D为多少，并且给出所有的错排方案。

定义:f(n)=(n-1)*( f(n-1) + f(n-2) )，f(1)=0 , f(2)=1

• [1 ] 当第k个人的贺卡放在第一个人的位置上时，剩下的问题就是n-2错排问题，即D(n-2)。
• [2 ] 当第k个人的贺卡不放在第一个人的位置上时，我们可以把第一个人的位置看作第k个人的位置（因为第k个人的贺卡根据前提条件不能放在上面），剩下的问题就是n-1错排问题，即D(n-1)。k有（n-1）种情况。

#include 
#define MAXN 20+10
#define ll long long
using namespace std;
ll cc(ll n, ll m){
    ll ans=1; 
    for(ll i=n, k=1; k<=m; k++, i--){
        ans*=i;
    }
    for(int i=1; i<=m; i++){
        ans/=i;
    }
    return ans;
}
int main( ){
    ll n, m, a[MAXN];
    a[2]=1, a[3]=2;
    for(int i=4; i>n>>m){
        ll ans=cc(n, n-m)*a[m];
        cout << ans << endl;
    }
    return 0;
}

• 数的划分

题目描述 将整数n分成k份，且每份不能为空，任意两个方案不相同(不考虑顺序)。

例如：n=7，k=3，下面三种分法被认为是相同的。

1,1,5; 1,5,1; 5,1,1;

问有多少种不同的分法。

输入输出格式 输入格式： n,k (6

输出格式： 11个整数，即不同的分法。

输入输出样例 输入样例#1 7 3 输出样例#1 4

说明 四种分法为 1,1,5; 1,2,4; 1,3,3; 2,2,3.

解析：
利用DP，把i平均分成j份，从中再找出数字规律，（如i,j的关系），即可。

我们用dp[i][j]来表示i有几个数，j来表示分成几份，dp[i][j]就表示i个数被分成j份。显然，当i=j时，只有一种情况;当i 最后，我们来想如果这k个数中不含1时，（如2,2,3），我们就必须将每个数都减1，就成了1,1,2，这时和为4，不够为7，因此，我们还要将地i-1里面j-1的数，用来相加，但是，第j个数必须为1，得dp[i-1][j-1].
综上所述，得转移态方程：dp[i][j]=dp[i-j][j]+dp[i-1][j-1];
这样，可以简化程序。

#include 
using namespace std;
int n,k;
int dp[1000][1000];
int main() {
	cin>>n>>k;
	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			dp[i][j]=dp[i-j][j]+dp[i-1][j-1];
		}
	}
	cout<

• 青蛙的约会
  两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。

我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。

这道题变量名太多了，让我本来简短的代码，变得十分混乱。
这哼明显是个一次不定方程，函数部分如下：
这是根据裴蜀定理得出的模板。

long long f(long long a,long long b,long long &xx,long long &yy){
	if(b==0){
		xx=1,yy=0;
		return a;
	}
	cnt=f(b,a%b,xx,yy);
	long long t=xx;
	xx=yy;
	yy=t-a/b*yy;
	return cnt;
}

裴蜀定理：

线性不定方程ax+by=1有解的充要条件是 a,b互质。
线性不定方程 ax+by=c有解的充要条件是 c=gcd(a,b)。
线性不定方程要么无解，要么有无数个解。
接下来，就要根据题目描述是算出其结果。
因为x-y为两只青蛙的纬度距离,m-n为两只青娃相差跳米数。
于是得出：[（x-y）+跳的次数*（m-n）]%l=0这一方程。
设(m-n)=A,k=X,(a-b)+Y,l=B,(x-y)=K
此时再套用求最小整数解的公式
((xx(s/cnt))%(l/cnt)+(l/cnt))%(l/cnt)

#include
using namespace std;
long long cnt,xx,yy;
long long f(long long a,long long b,long long &xx,long long &yy){
	if(b==0){
		xx=1,yy=0;
		return a;
	}
	cnt=f(b,a%b,xx,yy);
	long long t=xx;
	xx=yy;
	yy=t-a/b*yy;
	return cnt;
}
int main(){
	long long a,b,x,y,l;
	cin>>a>>b>>x>>y>>l;
	long long t=y-x,s=a-b;
	if(t<0){
		t=-t;
		s=-s;
	}
	f(t,l,xx,yy);
	if(s%cnt!=0)cout<<"Impossible";
	else cout<<((xx*(s/cnt))%(l/cnt)+(l/cnt))%(l/cnt);
	return 0;
}

TWO.组合数学

容斥原理

在计数时，必须注意没有重复，没有遗漏。
为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包
含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又
无重复，这种计数的方法称为容斥原理。
典型例子：公元纪年中的闰年；前缀和->区间和；二维前缀和。

抽屉原理

• 把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件

• 把（m*n－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体。

• 越不平均，则原理越明显；

• 类似的计数问题，选最平均的情况分析即可。

习题

小朋友的球
组合数问题
栈
球迷买彩票问题
墙壁涂色
三只小猪
排列计数

讲解（节选）

• 栈

题目背景
栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作，即poppop（从栈顶弹出一个元素）和pushpush（将一个元素进栈）。
栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。
题目描述
宁宁考虑的是这样一个问题：一个操作数序列，1,2,…,n1,2,…,n（图示为1到3的情况），栈AA的深度大于nn。
现在可以进行两种操作，
将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的pushpush操作）
将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的poppop操作）
使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由1 2 3123生成序列2 3 1231的过程。
（原始状态如上图所示）

你的程序将对给定的nn，计算并输出由操作数序列1,2,…,n1,2,…,n经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数n(1≤n≤18)n(1≤n≤18)
输出格式
输出文件只有11行，即可能输出序列的总数目
输入输出样例
输入 #1 复制
3
输出 #1 复制
5

#include
using namespace std;
int n,ans;
int dp[1000]={1,1,2,5,14,42,132,429,1430,
4862,16796,58786,208012,742900,2674440,9694845,35357670,
129644790,477638700,1767263190,6564120420,
24466267020,91482563640,343059613650,1289904147324,4861946401452};
int main(){
	cin>>n;
	cout<

• 球迷购票问题

题目背景
盛况空前的足球赛即将举行。球赛门票售票处排起了球迷购票长龙。
按售票处规定，每位购票者限购一张门票，且每张票售价为50元。在排成长龙的球迷中有N个人手持面值50元的钱币，另有N个人手持面值100元的钱币。假设售票处在开始售票时没有零钱。试问这2N个球迷有多少种排队方式可使售票处不致出现找不出钱的尴尬局面。
题目描述
例如当n=2是，用A表示手持50元面值的球迷，用B表示手持100元钱的球迷。则最多可以得到以下两组不同的排队方式，使售票员不至于找不出钱。
第一种:A A B B
第二种:A B A B
[编程任务]
对于给定的n (0≤n≤20),计算2N个球迷有多少种排队方式，可以使售票处不至于找不出钱。
输入格式
一个整数，代表N的值
输出格式
一个整数，表示方案数
输入输出样例
输入 #1 复制
2
输出 #1 复制
2
说明/提示
必开QWORD
测试：N=15
回溯:1秒（超时）
模拟栈：大于10分钟
递归算法：1秒（超时）
动态规划：0 MS
组合算法：16 MS

#include
using namespace std;
int n;
long long dp[500][500];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		dp[i][0]=1;
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			dp[i][j]=dp[i-1][j]+dp[i][j-1];
		} 
	}
	cout<