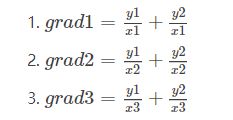灵活使用Tensorflow执行梯度下降算法
之前写过有关tensorflow中各种梯度的意义了,这里结合一下梯度下降算法,讲一下如何使用tensorflow进行相关梯度下降算法的实验。
还是再啰嗦一遍吧。。嫌不够仔细的可以参见:
https://blog.csdn.net/edward_zcl/article/details/90345318
声明:
- 参考官方文档
- 参考tensorflow学习笔记(三十)
- 关于神经网络中的梯度计算,推荐吴恩达的deeplearning公开课
tf.gradients()
在tensorflow中,tf.gradients()的参数如下:
tf.gradients(ys, xs,
grad_ys=None,
name='gradients',
colocate_gradients_with_ops=False,
gate_gradients=False,
aggregation_method=None,
stop_gradients=None)
先不给出参数的意义~
对求导函数而言,其主要功能即求导公式:∂y∂x∂y∂x都是tensor。
更进一步,tf.gradients()接受求导值ys和xs不仅可以是tensor,还可以是list,形如[tensor1, tensor2, …, tensorn]。当ys和xs都是list时,它们的求导关系为:
gradients()adds ops to the graph to output the derivatives ofyswith respect toxs. It returns a list ofTensorof lengthlen(xs)where each tensor is thesum(dy/dx)for y inys.
意思是:
tf.gradients()实现ys对xs求导- 求导返回值是一个list,list的长度等于
len(xs) - 假设返回值是[grad1, grad2, grad3],
ys=[y1, y2],xs=[x1, x2, x3]。则,真实的计算过程为:
基础实践
以线性回归为例,实践tf.gradients()的基础功能。线性回归:y=3×x+2y=3×x+2
import numpy as np
import tensorflow as tf
sess = tf.Session()
x_input = tf.placeholder(tf.float32, name='x_input')
y_input = tf.placeholder(tf.float32, name='y_input')
w = tf.Variable(2.0, name='weight')
b = tf.Variable(1.0, name='biases')
y = tf.add(tf.multiply(x_input, w), b)
loss_op = tf.reduce_sum(tf.pow(y_input - y, 2)) / (2 * 32)
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(loss_op)
'''tensorboard'''
# gradients_node = tf.gradients(loss_op, w)
# print(gradients_node)
# tf.summary.scalar('norm_grads', gradients_node)
# tf.summary.histogram('norm_grads', gradients_node)
# merged = tf.summary.merge_all()
# writer = tf.summary.FileWriter('log')
init = tf.global_variables_initializer()
sess.run(init)
'''构造数据集'''
x_pure = np.random.randint(-10, 100, 32)
x_train = x_pure + np.random.randn(32) / 10 # 为x加噪声
y_train = 3 * x_pure + 2 + np.random.randn(32) / 10 # 为y加噪声
for i in range(20):
_, gradients, loss = sess.run([train_op, gradients_node, loss_op],
feed_dict={x_input: x_train[i], y_input: y_train[i]})
print("epoch: {} \t loss: {} \t gradients: {}".format(i, loss, gradients))
sess.close()
输出:
epoch: 0 loss: 94.6083221436 gradients: [-187.66052]
epoch: 1 loss: 1.52120530605 gradients: [3.0984864]
epoch: 2 loss: 101.41834259 gradients: [241.91911]
...
epoch: 18 loss: 0.0215022582561 gradients: [-0.44370675]
epoch: 19 loss: 0.0189439821988 gradients: [-0.31349587]
可以看到梯度逐渐减小,说明模型逐渐收敛。同时也可以看到参数更新的方向主要是梯度下降的方向(尽管伴随着震荡)。
其他参数
其他参数都不太常用(其实是比较难用)。
grad_ys
grad_ys也是一个list,其长度等于len(ys)。这个参数的意义在于对xs中的每个元素的求导加权种。
假设grad_ys=[grad_ys1, grad_ys2, grad_ys3],xs=[x1, x2, x3],则list中每个元素,如grad_ys1的shape与xs的shape相同。
举个简单的例子:
import tensorflow as tf
w1 = tf.get_variable('w1', shape=[3])
w2 = tf.get_variable('w2', shape=[3])
w3 = tf.get_variable('w3', shape=[3])
w4 = tf.get_variable('w4', shape=[3])
z1 = 3 * w1 + 2 * w2+ w3
z2 = -1 * w3 + w4
grads = tf.gradients([z1, z2], [w1, w2, w3, w4], grad_ys=[[-2.0, -3.0, -4.0], [-2.0, -3.0, -4.0]])
with tf.Session() as sess:
tf.global_variables_initializer().run()
print(sess.run(grads))
如果不考虑参数grad_ys,输出应该是:
[array([ 3., 3., 3.], dtype=float32),
array([ 2., 2., 2.], dtype=float32),
array([ 0., 0., 0.], dtype=float32),
array([ 1., 1., 1.], dtype=float32)]
现在在权重参数grad_ys = [[-2.0, -3.0, -4.0], [-2.0, -3.0, -4.0]]的加权下,输出实际为:
[array([ -6., -9., -12.], dtype=float32),
array([-4., -6., -8.], dtype=float32),
array([0., 0., 0.], dtype=float32),
array([-2., -3., -4.], dtype=float32)]
stop_gradients
stop_gradients也是一个list,list中的元素是tensorflow graph中的op,一旦进入这个list,将不会被计算梯度,更重要的是,在该op之后的BP计算都不会运行。
例如:
a = tf.constant(0.)
b = 2 * a
c = a + b
g = tf.gradients(c, [a, b])
计算得g = [3.0, 1.0]。因为∂c∂a=∂a∂a+∂b∂a=3.0∂c∂a=∂a∂a+∂b∂a=3.0
但如果冻结operator a和b的梯度计算:
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
计算得g=[1.0, 1.0]。
上面的代码也等效于:
a = tf.stop_gradient(tf.constant(0.))
b = tf.stop_gradient(2 * a)
g = tf.gradients(a + b, [a, b])
接下来借助tensorflow来介绍一下梯度下降算法,这是目前深度学习的核心算法。
参考:
https://blog.csdn.net/flyfish1986/article/details/79128424
嗯。。说白了就是设定一个损失函数,对所有系数(变量)求解梯度,借助于tensorflow强大的计算图,大量使用链式法则,全导数,以及各种矩阵对矩阵的求导等等,然后再借助SGD及其其变体最小化算法,去利用得到的梯度修改那些系数(变量),使得损失函数最小化。。
这里着重介绍一下另外一种更灵活的用法。实现手动或者自动梯度下降算法。
参考:
https://blog.csdn.net/huqinweI987/article/details/82899910
tensorflow中提供了自动训练机制(见tensorflow optimizer minimize 自动训练和var_list训练限制),本文主要展现不同的自动梯度下降并附加手动实现。
learning rate、step、计算公式如下:
在预测中,x是关于y的变量,但是在train中,w是L的变量,x是不可能变化的。所以,知道为什么weights叫Variable了吧(强行瞎解释一发)
下面用tensorflow手动实现梯度下降:
为了方便写公式,下边的代码改了变量的命名,采用loss、prediction、gradient、weight、y、x等首字母表示,η表示学习率,w0、w1、w2等表示第几次迭代时w的值,不是多个变量。
loss=(y-p)^2=(y-w*x)^2=(y^2-2*y*w*x+w^2*x^2)
dl/dw = 2*w*x^2-2*y*x
代入梯度下降公式w1=w0-η*dL/dw|w=w0
w1 = w0-η*dL/dw|w=w0
w2 = w1 - η*dL/dw|w=w1
w3 = w2 - η*dL/dw|w=w2
初始:y=3,x=1,w=2,l=1,dl/dw=-2,η=1
更新:w=4
更新:w=2
更新:w=4
所以,本例x=1,y=3,dl/dw巧合的等于2w-2y,也就是二倍的prediction和label的差距。learning rate=1会导致w围绕正确的值来回徘徊,完全不收敛,这样写主要是方便演示计算。改小learning rate 并增加循环次数就能收敛了。
学习率大的话,大概就是这个效果
手动实现梯度下降Gradient Descent:
-
#demo4:manual gradient descent in tensorflow
-
#y label
-
y = tf.constant(
3,dtype = tf.float32)
-
x = tf.placeholder(dtype = tf.float32)
-
w = tf.Variable(
2,dtype=tf.float32)
-
#prediction
-
p = w*x
-
-
#define losses
-
l = tf.square(p - y)
-
g = tf.gradients(l, w)
-
learning_rate = tf.constant(
1,dtype=tf.float32)
-
#learning_rate = tf.constant(0.11,dtype=tf.float32)
-
init = tf.global_variables_initializer()
-
-
#update
-
update = tf.assign(w, w - learning_rate * g[
0])
-
-
with tf.Session()
as sess:
-
sess.run(init)
-
print(sess.run([g,p,w], {x:
1}))
-
for _
in range(
5):
-
w_,g_,l_ = sess.run([w,g,l],feed_dict={x:
1})
-
print(
'variable is w:',w_,
' g is ',g_,
' and the loss is ',l_)
-
-
_ = sess.run(update,feed_dict={x:
1})
结果:
learning rate=1
-
[[
-2.0],
2.0,
2.0]
-
variable
is w:
2.0 g
is [
-2.0]
and the loss
is
1.0
-
variable
is w:
4.0 g
is [
2.0]
and the loss
is
1.0
-
variable
is w:
2.0 g
is [
-2.0]
and the loss
is
1.0
-
variable
is w:
4.0 g
is [
2.0]
and the loss
is
1.0
-
variable
is w:
2.0 g
is [
-2.0]
and the loss
is
1.0
缩小learning rate
-
variable
is w:
2.9964619 g
is [
-0.007575512]
and the loss
is
1.4347095e-05
-
variable
is w:
2.996695 g
is [
-0.0070762634]
and the loss
is
1.2518376e-05
-
variable
is w:
2.996913 g
is [
-0.0066099167]
and the loss
is
1.0922749e-05
-
variable
is w:
2.9971166 g
is [
-0.0061740875]
and the loss
is
9.529839e-06
-
variable
is w:
2.9973066 g
is [
-0.0057668686]
and the loss
is
8.314193e-06
-
variable
is w:
2.9974842 g
is [
-0.0053868294]
and the loss
is
7.2544826e-06
-
variable
is w:
2.9976501 g
is [
-0.0050315857]
and the loss
is
6.3292136e-06
-
variable
is w:
2.997805 g
is [
-0.004699707]
and the loss
is
5.5218115e-06
-
variable
is w:
2.9979498 g
is [
-0.004389763]
and the loss
is
4.8175043e-06
-
variable
is w:
2.998085 g
is [
-0.0041003227]
and the loss
is
4.2031616e-06
-
variable
is w:
2.9982114 g
is [
-0.003829956]
and the loss
is
3.6671408e-06
-
variable
is w:
2.9983294 g
is [
-0.0035772324]
and the loss
is
3.1991478e-06
SGD:
注意,tensorflow中没有SGD(Stochastic Gradient Descent)这种梯度下降算法接口,SGD更像是一个喂数据的策略,而不是具体训练方法,按吴恩达教程,严格的说,SGD甚至一次只能训练一个样本,实际常见的更多是多个样本的mini-batch,只要喂数据的时候随机化就算是SGD(mini-batch)了。
Momentum梯度下降:
链接:Gradient Descent、Momentum、Nesterov的实现及直觉对比
-
#demo5.2 tensorflow momentum
-
-
-
y = tf.constant(
3,dtype = tf.float32)
-
x = tf.placeholder(dtype = tf.float32)
-
w = tf.Variable(
2,dtype=tf.float32)
-
#prediction
-
p = w*x
-
-
#define losses
-
l = tf.square(p - y)
-
g = tf.gradients(l, w)
-
Mu =
0.8
-
LR = tf.constant(
0.01,dtype=tf.float32)
-
-
init = tf.group(tf.global_variables_initializer(),tf.local_variables_initializer())
-
-
#update w
-
update = tf.train.MomentumOptimizer(LR, Mu).minimize(l)
-
-
with tf.Session()
as sess:
-
sess.run(init)
-
sess.run(tf.global_variables_initializer())
-
sess.run(tf.local_variables_initializer())
-
print(sess.run([g,p,w], {x:
1}))
-
for _
in range(
10):
-
w_,g_,l_ = sess.run([w,g,l],feed_dict={x:
1})
-
print(
'variable is w:',w_,
' g is ',g_,
' and the loss is ',l_)
-
-
sess.run([update],feed_dict={x:
1})
-
这是前几次迭代的数据,注意看,和下边的手动实现做对比
-
variable
is w:
2.0 g
is [
-2.0]
and the loss
is
1.0
-
variable
is w:
2.02 g
is [
-1.96]
and the loss
is
0.96040004
-
variable
is w:
2.0556 g
is [
-1.8888001]
and the loss
is
0.8918915
-
variable
is w:
2.102968 g
is [
-1.794064]
and the loss
is
0.80466646
-
variable
is w:
2.158803 g
is [
-1.682394]
and the loss
is
0.7076124
-
variable
is w:
2.220295 g
is [
-1.5594101]
and the loss
is
0.60793996
-
variable
is w:
2.2850826 g
is [
-1.4298348]
and the loss
is
0.5111069
-
variable
is w:
2.351211 g
is [
-1.2975779]
and the loss
is
0.42092708
-
variable
is w:
2.4170897 g
is [
-1.1658206]
and the loss
is
0.3397844
-
variable
is w:
2.4814508 g
is [
-1.0370984]
and the loss
is
0.26889327
下边是手动实现的,这里边有个速度v,是根据每一步的梯度累加的(注意,两步update必须分开执行,不能用tf.group)
-
#demo5.2:manual momentum in tensorflow
-
-
y = tf.constant(
3,dtype = tf.float32)
-
x = tf.placeholder(dtype = tf.float32)
-
w = tf.Variable(
2,dtype=tf.float32)
-
#prediction
-
p = w*x
-
-
#define losses
-
l = tf.square(p - y)
-
g = tf.gradients(l, w)
-
Mu =
0.8
-
LR = tf.constant(
0.01,dtype=tf.float32)
-
#v = tf.Variable(0,tf.float32)#error?secend param is not dtype?
-
v = tf.Variable(
0,dtype = tf.float32)
-
init = tf.global_variables_initializer()
-
-
#update w
-
update1 = tf.assign(v, Mu * v + g[
0] * LR )
-
update2 = tf.assign(w, w - v)
-
#update = tf.group(update1,update2)#wrong sequence!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
-
-
with tf.Session()
as sess:
-
sess.run(init)
-
print(sess.run([g,p,w], {x:
1}))
-
for _
in range(
10):
-
w_,g_,l_,v_ = sess.run([w,g,l,v],feed_dict={x:
1})
-
print(
'variable is w:',w_,
' g is ',g_,
' v is ',v_,
' and the loss is ',l_)
-
-
_ = sess.run([update1],feed_dict={x:
1})
-
_ = sess.run([update2],feed_dict={x:
1})
注意看前边这组数据,和tf自动实现的是一样的。
-
variable
is w:
2.0 g
is [
-2.0] v
is
0.0
and the loss
is
1.0
-
variable
is w:
2.0 g
is [
-2.0] v
is
-0.02
and the loss
is
1.0
-
variable
is w:
2.02 g
is [
-1.96] v
is
-0.0356
and the loss
is
0.96040004
-
variable
is w:
2.0556 g
is [
-1.8888001] v
is
-0.047367997
and the loss
is
0.8918915
-
variable
is w:
2.102968 g
is [
-1.794064] v
is
-0.05583504
and the loss
is
0.80466646
-
variable
is w:
2.158803 g
is [
-1.682394] v
is
-0.06149197
and the loss
is
0.7076124
-
variable
is w:
2.220295 g
is [
-1.5594101] v
is
-0.06478768
and the loss
is
0.60793996
-
variable
is w:
2.2850826 g
is [
-1.4298348] v
is
-0.06612849
and the loss
is
0.5111069
-
variable
is w:
2.351211 g
is [
-1.2975779] v
is
-0.06587857
and the loss
is
0.42092708
-
variable
is w:
2.4170897 g
is [
-1.1658206] v
is
-0.06436106
and the loss
is
0.3397844
-
variable
is w:
2.9999995 g
is [
-9.536743e-07] v
is
-4.7683734e-08
and the loss
is
2.2737368e-13
-
variable
is w:
2.9999995 g
is [
-9.536743e-07] v
is
-4.7683734e-08
and the loss
is
2.2737368e-13
-
variable
is w:
2.9999995 g
is [
-9.536743e-07] v
is
-4.7683734e-08
and the loss
is
2.2737368e-13
-
variable
is w:
2.9999995 g
is [
-9.536743e-07] v
is
-4.7683734e-08
and the loss
is
2.2737368e-13
-
variable
is w:
2.9999995 g
is [
-9.536743e-07] v
is
-4.7683734e-08
and the loss
is
2.2737368e-13
接下来是adagrad的例子:
adagrad有点使用Hessian矩阵的意思,不过用的是近似二次导数,因为真求出二次导数,在深度学习中代价还是很大的。
-
#demo6:adagrad optimizer in tensorflow
-
-
y = tf.constant(
3,dtype = tf.float32)
-
x = tf.placeholder(dtype = tf.float32)
-
w = tf.Variable(
2,dtype=tf.float32)
-
#prediction
-
p = w*x
-
-
#define losses
-
l = tf.square(p - y)
-
g = tf.gradients(l, w)
-
LR = tf.constant(
0.6,dtype=tf.float32)
-
optimizer = tf.train.AdagradOptimizer(LR)
-
update = optimizer.minimize(l)
-
init = tf.global_variables_initializer()
-
-
-
with tf.Session()
as sess:
-
sess.run(init)
-
#print(sess.run([g,p,w], {x: 1}))
-
for _
in range(
20):
-
w_,l_,g_ = sess.run([w,l,g],feed_dict={x:
1})
-
print(
'variable is w:',w_,
'g:',g_ ,
' and the loss is ',l_)
-
-
_ = sess.run(update,feed_dict={x:
1})
手动实现adagrad的例子(注意,两步update必须分开执行,不能用tf.group)
可以用依赖关系。
-
#demo6.2:manual adagrad
-
-
#with tf.name_scope('initial'):
-
-
y = tf.constant(
3,dtype = tf.float32)
-
x = tf.placeholder(dtype=tf.float32)
-
w = tf.Variable(
2,dtype=tf.float32,expected_shape=[
1])
-
second_derivative = tf.Variable(
0,dtype=tf.float32)
-
LR = tf.constant(
0.6,dtype=tf.float32)
-
Regular =
1e-8
-
-
#prediction
-
p = w*x
-
#loss
-
l = tf.square(p - y)
-
#gradients
-
g = tf.gradients(l, w)
-
#print(g)
-
#print(tf.square(g))
-
-
#update
-
update1 = tf.assign_add(second_derivative,tf.square(g[
0]))
-
g_final = LR * g[
0] / (tf.sqrt(second_derivative) + Regular)
-
update2 = tf.assign(w, w - g_final)
-
-
#update = tf.assign(w, w - LR * g[0])
-
-
init = tf.global_variables_initializer()
-
-
with tf.Session()
as sess:
-
sess.run(init)
-
print(sess.run([g,p,w], {x:
1}))
-
for _
in range(
20):
-
_ = sess.run(update1,feed_dict={x:
1.0})
-
w_,g_,l_,g_sec_ = sess.run([w,g,l,second_derivative],feed_dict={x:
1.0})
-
print(
'variable is w:',w_,
' g is ',g_,
' g_sec_ is ',g_sec_,
' and the loss is ',l_)
-
#sess.run(g_final)
-
-
_ = sess.run(update2,feed_dict={x:
1.0})
结果接近,可惜不完全一样,我也不知道optimizer中的参数都是多少,有没有正则化,太不透明了。
-
[[
-2.0],
2.0,
2.0]
-
variable
is w:
2.0 g
is [
-2.0] g_sec_
is
0.0
and the loss
is
1.0
-
variable
is w:
2.6 g
is [
-0.8000002] g_sec_
is
4.0
and the loss
is
0.16000007
-
variable
is w:
2.8228343 g
is [
-0.3543315] g_sec_
is
4.6400003
and the loss
is
0.0313877
-
variable
is w:
2.920222 g
is [
-0.15955591] g_sec_
is
4.765551
and the loss
is
0.006364522
-
variable
is w:
2.9639592 g
is [
-0.072081566] g_sec_
is
4.791009
and the loss
is
0.0012989381
-
variable
is w:
2.9837074 g
is [
-0.032585144] g_sec_
is
4.7962046
and the loss
is
0.0002654479
-
variable
is w:
2.9926338 g
is [
-0.014732361] g_sec_
is
4.7972665
and the loss
is
5.4260614e-05
-
variable
is w:
2.9966695 g
is [
-0.0066609383] g_sec_
is
4.7974834
and the loss
is
1.1092025e-05
-
variable
is w:
2.9984941 g
is [
-0.0030117035] g_sec_
is
4.797528
and the loss
is
2.2675895e-06
-
variable
is w:
2.999319 g
is [
-0.0013618469] g_sec_
is
4.797537
and the loss
is
4.6365676e-07
-
variable
is w:
2.9996922 g
is [
-0.0006155968] g_sec_
is
4.7975388
and the loss
is
9.4739846e-08
-
variable
is w:
2.9998608 g
is [
-0.0002784729] g_sec_
is
4.797539
and the loss
is
1.9386789e-08
-
variable
is w:
2.999937 g
is [
-0.00012588501] g_sec_
is
4.797539
and the loss
is
3.961759e-09
-
variable
is w:
2.9999716 g
is [
-5.6743622e-05] g_sec_
is
4.797539
and the loss
is
8.0495965e-10
-
variable
is w:
2.9999871 g
is [
-2.5749207e-05] g_sec_
is
4.797539
and the loss
is
1.6575541e-10
-
variable
is w:
2.9999943 g
is [
-1.1444092e-05] g_sec_
is
4.797539
and the loss
is
3.274181e-11
-
variable
is w:
2.9999974 g
is [
-5.2452087e-06] g_sec_
is
4.797539
and the loss
is
6.8780537e-12
-
variable
is w:
2.9999988 g
is [
-2.3841858e-06] g_sec_
is
4.797539
and the loss
is
1.4210855e-12
-
variable
is w:
2.9999995 g
is [
-9.536743e-07] g_sec_
is
4.797539
and the loss
is
2.2737368e-13
-
variable
is w:
2.9999998 g
is [
-4.7683716e-07] g_sec_
is
4.797539
and the loss
is
5.684342e-14
-
-
variable
is w:
2.0 g: [
-2.0]
and the loss
is
1.0
-
variable
is w:
2.5926378 g: [
-0.81472445]
and the loss
is
0.16594398
-
variable
is w:
2.816606 g: [
-0.3667879]
and the loss
is
0.033633344
-
variable
is w:
2.9160419 g: [
-0.1679163]
and the loss
is
0.0070489706
-
variable
is w:
2.9614334 g: [
-0.07713318]
and the loss
is
0.0014873818
-
variable
is w:
2.9822717 g: [
-0.035456657]
and the loss
is
0.00031429363
-
variable
is w:
2.9918494 g: [
-0.016301155]
and the loss
is
6.6431916e-05
-
variable
is w:
2.9962525 g: [
-0.0074949265]
and the loss
is
1.404348e-05
-
variable
is w:
2.998277 g: [
-0.0034461021]
and the loss
is
2.968905e-06
-
variable
is w:
2.9992077 g: [
-0.0015845299]
and the loss
is
6.2768373e-07
-
variable
is w:
2.9996357 g: [
-0.0007286072]
and the loss
is
1.327171e-07
-
variable
is w:
2.9998324 g: [
-0.00033521652]
and the loss
is
2.809253e-08
-
variable
is w:
2.999923 g: [
-0.0001540184]
and the loss
is
5.930417e-09
-
variable
is w:
2.9999645 g: [
-7.104874e-05]
and the loss
is
1.2619807e-09
-
variable
is w:
2.9999835 g: [
-3.2901764e-05]
and the loss
is
2.7063152e-10
-
variable
is w:
2.9999924 g: [
-1.5258789e-05]
and the loss
is
5.820766e-11
-
variable
is w:
2.9999964 g: [
-7.1525574e-06]
and the loss
is
1.2789769e-11
-
variable
is w:
2.9999983 g: [
-3.33786e-06]
and the loss
is
2.7853275e-12
-
variable
is w:
2.9999993 g: [
-1.4305115e-06]
and the loss
is
5.1159077e-13
-
variable
is w:
2.9999998 g: [
-4.7683716e-07]
and the loss
is
5.684342e-14
这个例子只供演示,真正体现Adagrad优势的,还得是多参数情形,单参数用Adagrad不能显现很大优势,Adagrad的一大优点,是能协调不同参数的学习速率,每个参数都被自己的“二次微分”约束,最后就公平了。
源码
进行梯度下降之后,其实对于计算机而言,可能还会有一些问题,比如数值计算问题,数值精度问题,无穷大无穷小以及loss的NaN问题等等。
除此之外,以防万一自己写错,或者调试监测方便的目的,一般会设置梯度检查,生成tensorboard或者log日志,打印相关信息等。
参考:机器学习算法的调试 —— 梯度检验(Gradient Checking)
https://blog.csdn.net/lanchunhui/article/details/51279293