OpenCV学习入门（三）：kmeans原理及代码

Kmeans是一种非监督的聚类方法，是最常用的聚类技术之一。kmeans尝试找到数据的自然类别，通过用户设定的类别个数K，它可以快速的找到“好的”类别中心，“好的”意味着聚类中心位于数据的自然中心。

（一）算法步骤

Kmeans算法一般步骤如下：

1、输入样本数据集合和用户指定的类别数K。

2、分配类别初始化中心点的位置（随机或指定）。

3、将每个样本点放入离它最近的聚类中心所在的集合。

4、移动聚类中心点到它所在集合的中心。

5、转到第3步，直到满足给定的收敛条件。

下图展示了kmeans到底是怎么工作的：

图1.（a）随机设置聚类中心然后将数据样本聚到离它最近的中心（b）将初始中心移动到新聚类集合所在中心（c）数据样本点根据最近邻规则重新聚到类别中心（d）聚类中心再次移到它所在新类别的中心

（二）Kmeans优缺点

Kmeans有以下几个优点：

1、是解决聚类问题的一种经典算法，算法简单、快速。

2、对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度是线性的，大约是O（nkt），其中n是所有样本的数目，k是簇的数目,t是迭代的次数。通常k<

3、该算法是收敛的（不会无限迭代下去）。

4、算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，而簇与簇之间区别明显时，它的聚类效果很好。

Kmeans也存在如下缺点：

1、只有在簇的平均值被定义的情况下才能使用，不适用于某些应用，如涉及有分类属性的数据不适用。它的前提假设是样本数据的协方差矩阵已经归一化。

2、虽然理论证明它是一定可以收敛的，但是不能保证是全局收敛，可能是局部收敛，这样的话找到的聚类中心不一定是最佳方案。

3、要求用户必须事先给出要生成的簇的数目K。对于同一个数据样本集合，选择不同的K值，得到的结果是不一样的，甚至是不合理的。

4、对中心初值敏感，对于不同的初始值，可能会导致不同的聚类结果。

5、对于"噪声"和孤立点数据敏感，少量的该类数据能够对平均值产生极大影响。

6、不适合于发现非凸面形状的簇，或者大小差别很大的簇。

改进的方法如下：

1、对样本数据进行归一化处理，这样就能防止某些大值属性的数据左右样本间的距离。给定一组含有n个数据的数据集，每个数据含有m个属性，分别计算每一个属性的均值、标准差对每条数据进行归一化。另外，距离度量选择也很重要。常见的距离度量方法包括：Euclidean距离（欧氏距离），Mahalanobis距离（马氏距离），余弦距离等。马氏距离：表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法，是尺度无关的。如果协方差矩阵为单位矩阵,那么马氏距离就退化为欧氏距离。余弦距离：不受指标刻度的影响，值域[-1,1]，值越大，差异越小。具体选择哪种距离度量，需要根据数据情况具体选择。

2、对于初始化中心/质心的改进：

选择适当的初始质心是kmeans算法的关键步骤。常见的方法是随机的选取初始质心（利用OpenCV中的随机函数），但是这样生成的聚类簇的质量常常很差。一种常用的解决方法是：多次运行，每次使用一组不同的随机初始质心，然后选取具有最小误差的平方和（SSE）的簇集。这种策略简单，但是效果可能不好，这取决于数据集和寻找的簇的个数。

第二种有效的方法是，取一个样本，并使用层次聚类技术对它聚类。从层次聚类中提取K个簇，并用这些簇的质心作为初始质心。该方法通常很有效，但仅对下列情况有效：（1）样本相对较小，例如数百到数千（层次聚类开销较大）；（2）K相对于样本大小较小

第三种选择初始质心的方法，随机地选择第一个点，或取所有点的质心作为第一个点。然后，对于每个后继初始质心，选择离已经选取过的初始质心最远的点。使用这种方法，确保了选择的初始质心不仅是随机的，而且是散开的。但是，这种方法可能选中离群点。此外，求离当前初始质心集最远的点开销也非常大。为了克服这个问题，通常该方法用于点样本。由于离群点很少（多了就不是离群点了），它们多半不会在随机样本中出现。计算量也大幅减少。

3、对于K值选择的改进：首先将类别数设为1，然后逐渐提高类别数直到某个上限，每次聚类都使用方法2保证是近似最佳结果。一般情况下，总方差会快速下降到达一个拐点，这意味着再增加一个新的聚类中心不会显著的较少总方差。在拐点处停止，保存此时的类别数。

4、对孤立点的改进：

     经典k均值算法中没有考虑孤立点。所谓孤立点都是基于距离的, 是数据集中与其最近邻居的平均距离最大的对象。基于距离法移除孤立点, 具体过程如下:

     首先扫描一次数据集, 计算每一个数据对象与其邻近对象的距离, 累加求其距离和, 并计算出距离和均值。如果某个数据对象的距离和大于距离和均值, 则视该点为孤立点。把这个对象从数据集中移除到孤立点集合中, 重复直到所有孤立点都找到。最后得到新的数据集就是聚类的初始集合。

5 收敛条件

一般是目标函数达到最优或者达到最大的迭代次数即可终止。对于不同的距离度量，目标函数往往不同。当采用欧式距离时，目标函数一般为最小化簇成员到其簇质心的距离的平方和。收敛的目标是：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。

（三）代码示例

以下代码说明：随机产生sampleCount（范围[1,1000]）个二维样本，随机产生clusterCount(范围[2,5])个类别，每个类别的样本数据都服从高斯分布，该高斯分布的均值是随机的，方差是固定的。然后对这sampleCount个样本数据使用kmeans算法聚类3次，取其中最好的一次作为最后的结果，最后将不同的类用不同的颜色显示出来。

// kmeans.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/core/core.hpp"
#include 

using namespace cv;
using namespace std;

// static void help()
// {
//     cout << "\nThis program demonstrates kmeans clustering.\n"
//             "It generates an image with random points, then assigns a random number of cluster\n"
//             "centers and uses kmeans to move those cluster centers to their representitive location\n"
//             "Call\n"
//             "./kmeans\n" << endl;
// }

int main(int /*argc*/, char** /*argv*/)
{
	const int MAX_CLUSTERS = 5; //最大聚类数目
	Scalar colorTab[] =         //为最大的5种聚类分配5种不同的颜色，用以区分不同类的数据
	{
		Scalar(0, 0, 255),
		Scalar(0, 255, 0),
		Scalar(255, 100, 100),
		Scalar(255, 0, 255),
		Scalar(0, 255, 255)
	};

	Mat img(500, 500, CV_8UC3);  //建立一个500X500，3通道的彩色图
	RNG rng(12345); //随机数产生器
	for (;;)
	{
		int k, clusterCount = rng.uniform(2, MAX_CLUSTERS + 1);		//在[2,6]之间产生均匀随机数作为该次实验聚类个数，保证至少有两个及以上待聚类，才能体现kmeans方法
		int i, sampleCount = rng.uniform(1, 1001);					//在[1,1001]之间均匀随机产生所有样本点
		Mat points(sampleCount, 1, CV_32FC2), labels;				//存放样本点，是sampleCount行2通道的行向量

		clusterCount = MIN(clusterCount, sampleCount);				//保证聚类数小于数据样本数
		Mat centers(clusterCount, 1, points.type());				//用来存储聚类后的中心点

		/* generate random sample from multigaussian distribution */
		for (k = 0; k < clusterCount; k++) 
		{
			Point center;
			center.x = rng.uniform(0, img.cols);					//均匀随机产生初始化聚类中心
			center.y = rng.uniform(0, img.rows);
			Mat pointChunk = points.rowRange(k*sampleCount / clusterCount,	//每个聚类中样本数目都是sampleCount / clusterCount
				k == clusterCount - 1 ? sampleCount :				//K至少能取到0,1，保证有两个及以上待聚类
				(k + 1)*sampleCount / clusterCount);				
			//每个聚类的随机初始化中心作为均值，方差都相等
			rng.fill(pointChunk, CV_RAND_NORMAL, Scalar(center.x, center.y), Scalar(img.cols*0.05, img.rows*0.05));
		}

		randShuffle(points, 1, &rng);								//随机打乱points里面的样本点，注意points和pointChunk是共用数据的。
		//聚类3次，取结果最好的那次，KMEANS_PP_CENTERS表示初始化中心使用Arthur and Vassilvitskii的kmeans++初始化方法。
		kmeans(points, clusterCount, labels,
			TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 10, 1.0),
			3, KMEANS_PP_CENTERS, centers);  

		img = Scalar::all(0);
		//遍历所有点，根据不同聚类中心使用不同的颜色绘制出来
		for (i = 0; i < sampleCount; i++)
		{
			int clusterIdx = labels.at(i);
			Point ipt = points.at(i);
			circle(img, ipt, 2, colorTab[clusterIdx], CV_FILLED, CV_AA);
		}

		imshow("clusters", img);

		char key = (char)waitKey();     
		if (key == 27 || key == 'q' || key == 'Q') // 退出条件：按键'ESC','q','Q'
			break;
	}

	return 0;
}

（四）代码说明

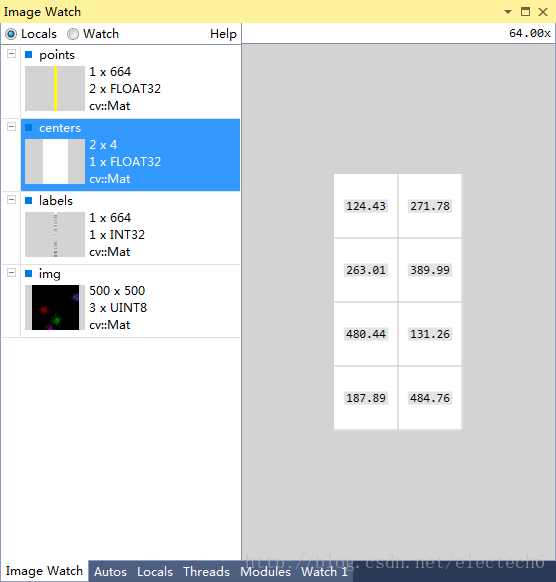
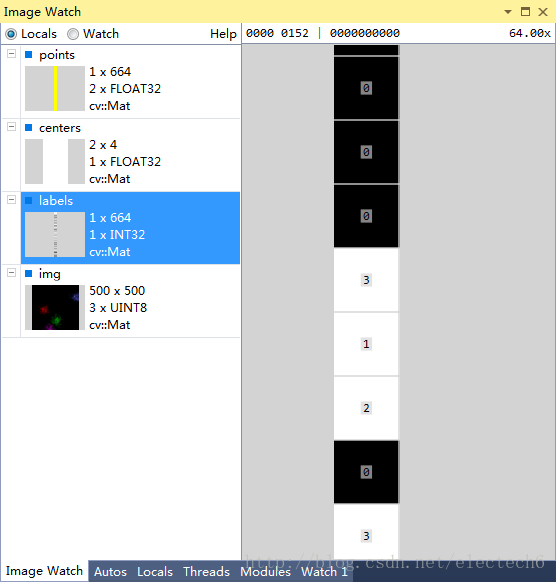
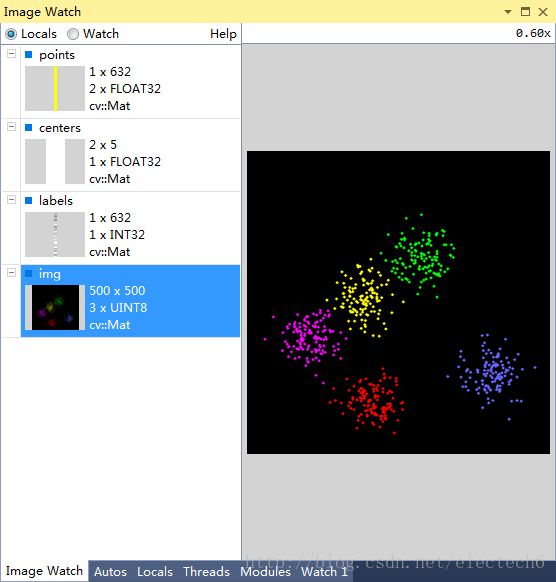
我用image watch 观察了聚类的过程中变量，具体如下：
                               

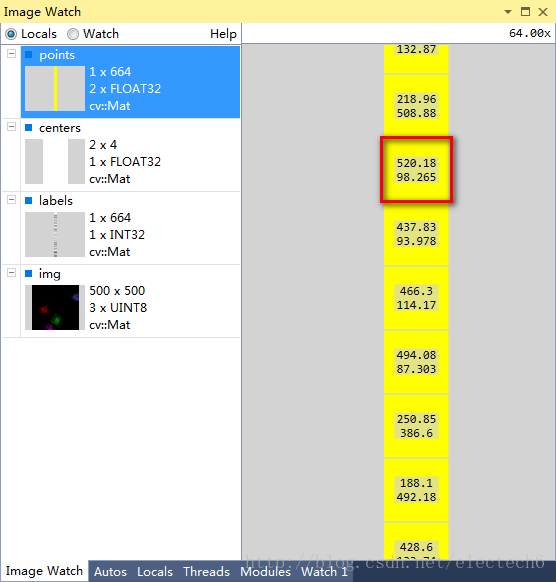
                  图2 输入的样本数据，高斯随机得到，总共664行，每行是一个二维数据，表示样本点的坐标

图3 最后得到的聚类中心

图4 样本数据最后的标号

图5 最终聚类结果图示