动态规划——编辑距离
1. 实践题目
编辑距离
2.问题描述
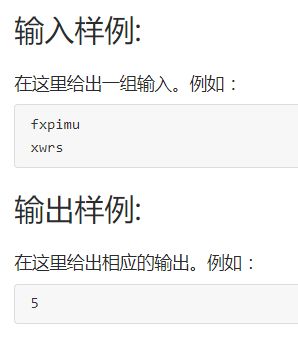
设A和B是2个字符串。要用最少的字符操作将字符串A转换为字符串B。这里所说的字符操作包括 (1)删除一个字符; (2)插入一个字符; (3)将一个字符改为另一个字符。 将字符串A变换为字符串B所用的最少字符操作数称为字符串A到 B的编辑距离,记为d(A,B)。对于给定的字符串A和字符串B,计算其编辑距离 d(A,B)。
3. 算法描述
这是一个动态规划问题。我们定义一个二维数组d[i][j]来保存这些编辑最小操作,它表示将串a[0:i-1]转变为b[0:j-1]的最小步骤(a[]和b[]是两个字符数组,从下标0开始初始化)。
然后我们分情况先讨论:
当i = 0时:a串为空,那么转变为b串就是不断添加字符,d[0][j] = j。
当j = 0时:b串为空,那么转变为b串就是不断删除字符,d[i][0] = i。
接下来是一般情况:我们考虑到字符的操作有三种,分别是删除、增加和替换,那么它们的操作就是在前一步的操作下以最少的次数增删改。现在分三种情况:
1)假设把a[1:i] -> b[1:j-1]要x个步骤,那只要在b[j]增加a[i]后面就搞定了,那就需要x+1步操作。
2)假设把a[1:i-1] -> b[1:j]要x个步骤,那么只要在删除a[i]就好了,需要x+1步操作。
3)假设把a[1:i-1] -> b[1:j-1]要x个步骤,那么只需要把a[i]替换为b[j]就ok了,那就需要x+1步操作。如果a[i] == b[j],只需要x步。
所以填表法的思想来讲,就是从上面三种情况中选最小的,填入表格中。
递归公式: 1<=i<=length_a, 1<=j<=length_b
d[i][j] =min(d[i-1][j-1], d[i][j-1]+1, d[i-1][j]+1), a[i-1] == b[j-1]时
(之前和同学讨论的时候,有人提到在上面这种情况的时候,只需要让d[i][j] = d[i-1][j-1]就可以了,我交了一下确实也可以……但是我找不出特例。如果从这三个中取最小反而更好理解,解释得通,也让这个递归公式有通用性,我觉得)
d[i][j] =min(d[i-1][j-1]+1, d[i][j-1]+1, d[i-1][j]+1), a[i-1] != b[j-1]时
最优值:d[length_a][length_b]
我们初始化d[][]数组
| x | w | r | s | ||
| 0 | 1 | 2 | 3 | 4 | |
| f | 1 | 1 | 1 | 2 | 3 |
| x | 2 | ||||
| p | 3 | ||||
| i | 4 | ||||
| m | 5 | ||||
| u | 6 |
其他以此类推。
最优值:d[length_a][length_b]
4.算法时间及空间复杂度分析
时间复杂度:其实是对一个二维数组d[length_a+1][length_b+1]进行填写的花销,其他的只是一些简单的加减运算和比较,所以双重循环对算法的花销贡献最大,时间复杂度为O(mn)。
空间复杂度:因为用到了二维数组d[][],故为O(mn)。
5.代码
#include
#include
using namespace std;
int d[2005][2005];
/*
输入的两个字符数组为a[], b[],从下标为0开始初始化
长度分别为length_a, length_b
数组d[m][n]存放从a[1:m] 变为 b[1:n]所需要的最少操作
递归公式:
d[i][j] = 0, i=0或j=0 时(即数组的第一行和第一列均为0)
1<=i<=length_a, 1<=j<=length_b
d[i][j] = d[i-1][j-1], a[i-1] == b[j-1]
d[i][j] = min(d[i-1][j-1]+1, d[i][j-1]+1, d[i-1][j]+1), a[i-1] != b[j-1]
最优值:d[length_a][length_b]
*/
int min(int a, int b, int c){
int temp = a;
if(temp > b){
temp = b;
}
if(temp > c){
temp =c;
}
return temp;
}
int edit(char *a, char *b){
int length_a = strlen(a);
int length_b = strlen(b);
for(int i = 0; i <= length_a; i++){
d[i][0] = i;
}
for(int i = 0; i <= length_b; i++){
d[0][i] = i;
}
for(int i = 1; i <= length_a; i++){
for(int j = 1; j <= length_b; j++){
if(a[i-1] == b[j-1]){
//d[i][j] = d[i-1][j-1];
d[i][j] = min(d[i-1][j-1], d[i][j-1]+1, d[i-1][j]+1);
}
else{
d[i][j] = min(d[i-1][j-1]+1, d[i][j-1]+1, d[i-1][j]+1);
}
}
}
return d[length_a][length_b];
}
int main(){
char a[2000], b[2000];
cin>>a>>b;
cout<