退而求其次(4)——椭圆中的最大矩形

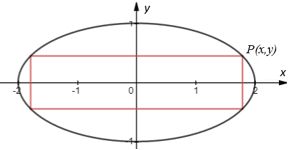
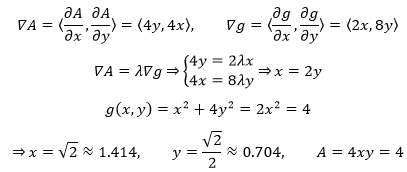　　在椭圆x²+4y²=4 中有很多内接的矩形，这些矩形的边平行于x轴和y轴，找出它们中面积最大的一个。

　　先作图，椭圆的中心在原点，其内接矩形的中心也在原点。设矩形的其中一点内接椭圆于P(x,y) ， P在第一象限：

　　矩形的两条边长分别是2x和2y，面积是A=4xy 。还知道x和y都在椭圆上，因此问题可以转换为约束条件下的极值：

数学方案

　　最直接的方案是使用拉格朗日乘子法：

　　由于拉格朗日乘子法无法确定最值的类型，所以还要计算函数边界值。当P在椭圆上移动时，如果正好落在x轴上，则长方形退化成直线，此时面积是0；另一个边界值是P落在y轴上，面积也是0。所以判定4是面积的最大值，P的坐标是(1.414, 0.707)

抛开数学的遗传算法

　　格朗日乘子法很简单，但前提是需要了解偏导、梯度、拉格朗日乘子等一系列前置知识，而遗传算法的优点是不需要复杂的数学知识，可以直接对问题编程求解，这对庞大的程序员群体来说无疑是个福音。

　　可以通过椭圆得到x和y的关系：

　　矩形的面积可以写成：

　　只需要对x进行基因编码就可以利用遗传算法求得最优解。在编写代码前，可以考虑是否能够去掉影响算法运行速度和计算精度根号。

　　由于x和y都大于等于0，所以当4xy达到最大值时，(4xy)²也将达到最大。在求最值问题时，常系数起不到任何作用，因此求(4xy)²的最大值相当于求x²y²的最大值。结合x和y的关系，原问题转换为：

　　现在看起来简单多了。

　　我们把问题精确到小数点后3位，从0.000到1.000之间有999个数，由于999转换成二进制是1111100111，因此可以使用10位二进制基因编码表示y。

　　代码如下：

  1 import math
  2 import random
  3 import numpy as np
  4 import matplotlib.pyplot as plt
  5
  6 MAX, MIN = 0.999, 0 # y的最大值和最小值
  7 CODE_SIZE = 10 # 基因编码长度
  8 POPULATION_SIZE = 20 # 种群数量
  9
 10 def print_solution(code):
 11     '''
 12      打印解决方案
 13     :param code: 基因编码
 14     '''
 15     x, y, A = decode(code)
 16     print('x = {0}, y = {1}, A = {2}'.format(x, y, A))
 17
 18 def decode(code:list):
 19     '''
 20     解码
 21     :param code: 基因编码
 22     :return: x,y,4xy （x,y都放大了1000倍）
 23     '''
 24     y = int(''.join(code), 2) * 0.001  # 将code转换成十进制数
 25     if y > MAX:  # y超过了边界
 26         return -1, -1, -1
 27     x = math.sqrt(4 - 4 * (y ** 2)) # x = sqrt(4 -4(y^2))
 28     # 使用退一法保留小数点后三位有效数字
 29     x, y = float('%.3f' % x), float('%.3f' % y)
 30     return x, y, 4 * x * y
 31
 32 def fitness_fun(code):
 33     ''' 适应度函数 '''
 34     return decode(code)[2]
 35
 36 def max_fitness(population):
 37     ''' 种群中的最优适应个体 '''
 38     return max([fitness_fun(code) for code in population])
 39
 40 def init_population():
 41     ''' 构造初始种群 '''
 42     population = []
 43     for i in range(POPULATION_SIZE):
 44         population.append(random.choices(['0', '1'], k=CODE_SIZE))
 45     return population
 46
 47 def selection(population):
 48     ''' 精英选择策略'''
 49     # 按适应度从大到小排序
 50     pop_parents = sorted(population, key=lambda x: fitness_fun(x), reverse=True)
 51     # 选择种群中适应度最高的40%作为精英
 52     return pop_parents[0: int(POPULATION_SIZE * 0.4)]
 53
 54 def crossover(population):
 55     ''' 单点交叉 '''
 56     pop_new = []  # 新种群
 57     code_len = len(population[0])  # 基因编码的长度
 58     for i in range(POPULATION_SIZE):
 59         p = random.randint(1, code_len - 1)  # 随机选择一个交叉点
 60         r_list = random.choices(population, k=2)  # 选择两个随机的个体
 61         pop_new.append(r_list[0][0:p] + r_list[1][p:])
 62     return pop_new
 63
 64 def mutation(population):
 65     '''单点变异'''
 66     code_len = len(population[0])  # 基因编码的长度
 67     mp = 0.2 # 变异率
 68     for i, r in enumerate(population):
 69         if random.random() < mp:
 70             p = random.randint(0, code_len - 1)  # 随机变异点
 71             r[p] = '1' if r[p] == '0' else '1'
 72             population[i] = r
 73
 74 def ga():
 75     ''' 遗传算法 '''
 76     population = init_population() # 构建初始化种群
 77     max_fit = max_fitness(population) # 种群最优个体的适应度
 78     max_fit_list = [max_fit]  # 每一代种群的最优适应度
 79     i = 0
 80     while i < 5: # 如果连续5代没有改进，结束算法
 81         pop_next = selection(population) # 选择种群
 82         pop_new = crossover(pop_next) # 交叉
 83         mutation(pop_new) # 变异
 84         max_fit_new = max_fitness(pop_new) # 新种群中最优个体的适应度
 85         if max_fit < max_fit_new:
 86             max_fit = max_fit_new
 87             i = 0
 88         else:
 89             i += 1
 90         population = pop_new
 91         max_fit_list.append(max_fit_new)
 92     # 按适应度值从大到小排序
 93     population = sorted(population, key=lambda x: fitness_fun(x), reverse=True)
 94     # 返回最优的个体和每一代种群中最优个体的适应度
 95     return population[0], max_fit_list
 96
 97 def pop_curve(max_fit_list):
 98     ''' 显示种群进化曲线 '''
 99     x = np.arange(1, len(max_fit_list) + 1, 1)
100     y = np.array(max_fit_list)
101     plot = plt.plot(x, y, '-')
102     plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
103     plt.title('种群进化曲线')
104     plt.xlabel('种群代数')
105     plt.ylabel('种群总成本')
106     plt.show()
107
108 if __name__ == '__main__':
109     # code = ['1','0','1','1','0','0','0','0','1','1']  # 707的二进制基因编码
110     # print_solution(code)
111     best, max_fit_list = ga()
112     print_solution(best)
113     pop_curve(max_fit_list)

　　decode方法先将y的基因编码转换成对应的十进制数，之后乘以0.001变成相应的小数。适应度函数的值是矩形的面积。遗传算法的主体方法ga()除了得到最优个体外，还额外返回了每一代种群中最优个体的适应度，以便展示种群进化曲线。在实际应用中，可以通过观察进化曲线来观察算法在哪里收敛，从而调整算法的终止条件。

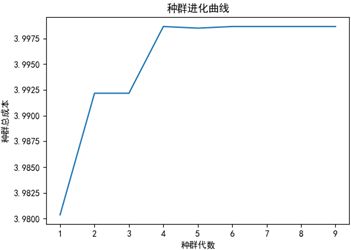
　　种群的进化曲线

　　可以看到，算法收敛的相当快。一种可能的结果是：

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”