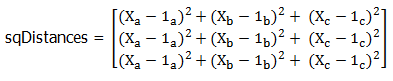【机器学习笔记】来吧！解析k-NN

序：

　　监督型学习与无监督学习，其最主要区别在于：已知的数据里面有没有标签（作为区别数据的内容）。

　　监督学习大概是这个套路：

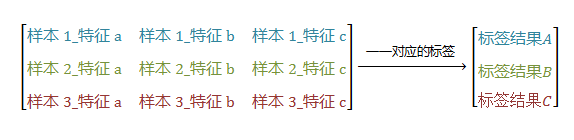
　　1.给定很多很多数据（假设2000个图片），并且给每个数据加上标签（与图片一一对应的2000个标签数据），以上统称为样本数据；

　　2.取一定比例的样本数据集（剩下的数据还有别的作用，此处一般可设为取90%）放入到训练模型，训练之后得到一个目标模型；

　　3.出模型后，还需要确定模型（识别或分类等的）准确度，

　　　此时，需要投入测试数据集（即剩下那10%的数据集），从模型得到结果之后比较对应的标签值，以得到准确率如何。

 

一、k-NN原理

　　k-邻近（k-NearestNeighbor）：

　　　　通过近邻数据的类别来对无标签样本进行分类。

　　　　首先找到样本集中与输入样本数据差距最小的k个样本，然后根据这k个样本里哪个分类最多从而确定输入样本的分类是什么。

　　　　k-NN是一种基于实例的学习，其分类并非取决于内在模型，而是对带标签的测试集进行参考比较，是一种非归纳的方法。

 

　　字面上应该是很好理解的，我跟着《机器学习实战》跑第二章代码，发现代码还是得写得很细致。

　　我用的是Win7 Python3.6的环境，与书本的语言版本可能不同，不过下文贴出的代码都有修改，验证能跑的。

　　有意思的是一些类库的方法，至于如何看待这些类库，一个原则：“只要觉得合理存在的就应该有”。

 

　　已知有数据：

　　求待预测数据与 已作分类的各个样本 的差距（对，就是粗暴的减法）：

　　据矩阵加减法的格式要求，样本数据要稍作处理（使用numpy提供的tile()），结果设为diffMat：

　　避免出现负值，加个平方（是点乘，仅矩阵内的数值操作平方）：

　　此时diffMatsq是1000 * 3的矩阵，内容是待测样本X与所有样本的差距，但是不同特征之间如何看待这个差距呢？每个特征信息对于分类结果的影响，可能是不一样的，这里就涉及到归一化、赋予权重的问题，但此处仅为捋过程，暂且不做处理，粗暴地当每个特征的影响程度都是平等的。现取行之和作为矩阵sqDistances：

　　numpy里的 .sum(axis = 1) 处理过后，会为矩阵转置，也即矩阵大小变化：n * m –> n * 1 –> 1 * n 。（注：sum函数中axis = 0 是一列当中的每行数据相加，axis = 1 是一行中的每列数据相加）

　　接下来就很明显了，取前 k 个最小差距的样本，这里用到一个很有意思的函数 .argsort()，它可以返回从小到大排序的索引值。注意，是索引值。下表为一个数值demo：

索引号	0	1	2	3	4
差值	1.4	0.4	0.1	0	2.5
.argsort() 设为sortedDistIndicies	3	2	1	0	4

　　这样解读第三行，.argsort() 就发光发热了：

　　第一个最小的数值，索引编号在3；第二小的索引号在2，以此类推。

　　回归正题，k-NN是要干嘛？是时候展现k-NN的技术了：

　　取到前k个最小差距的样本，再记录这个样本的标签值，最后统计哪个标签出现次数最多，就判断带分类样本为该标签分类结果。

    for i in range(k):
        voteIlabel  =  labels[sortedDistIndicies[i]]
        classCount[voteIlabel]  =  classCount.get(voteIlabel, 0) + 1

　　这个 i 表面上是k里面的第几个，但实际上，也是表示第几个最小差值，那个标签索引就在 sortedDistIndicies 里面找。

　　这波操作结束之后，再排序（classCount是字典类型，{标签,出现次数}），返回出现次数最多的标签值就完事了。

 

二、python3.6实现k-NN

　1.踏踏实实，一个勤恳的宝宝：

def classify0(inX, dataSet, labels, k):                   # inX：待分类目标，dataSet：数据集，labels：数据集对应标签
    dataSetSize = dataSet.shape[0]                        # 1000
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet       # 1000 * 3
    sqDiffMat = diffMat ** 2                              # 矩阵内数值平方 1000 * 3
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5
    sortedDistIndicies = distances.argsort()
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)
    return sortedClassCount[0][0]

 

　2. Scikit-learn，k-NN带回家

　　既然“只要觉得合理存在，就应该存在”，那么k-NN有没有省事点调用的方法呢？

　　Scikit-learn类库帮助你！pip install sklearn即刻免费带回家 ~ 只要添加引用：

from sklearn.neighbors import KNeighborsClassifier as knn

　　麻麻再也不担心我不会写啦：

import numpy as np
from sklearn.neighbors import KNeighborsClassifier as knn
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def knnDemo(X, y, k):
    res = 0.05
    k1 = knn(n_neighbors = k, p = 2, metric = 'minkowski')
    k1.fit(X,y)

    # sets up the grid
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1        # 第一行数据最值
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1        # 第二行数据最值
                                                                 # xx1，xx2是伪造的数据①
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, res), np.arange(x2_min, x2_max, res))

    Z = k1.predict(np.array([xx1.ravel(), xx2.ravel()]).T)       # 括号里矩阵大小 2 * 9856
    Z = Z.reshape(xx1.shape)                                     # 9856个结果。因为下文是按照xx1和xx2构建的直角坐标系，所以点的(x,y)这样换算

    # creates the color map
    cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF']) # 3个标签，3个颜色
    cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])

    # plots the decision surface
    plt.contourf(xx1, xx2, Z, alpha = 0.4, cmap = cmap_light)    # 渲染背景色
    plt.xlim(xx1.min(), xx1.max())                               # x、y轴起始
    plt.ylim(xx2.min(), xx2.max())

    # plots the samples
    for idx, c1 in enumerate(np.unique(y)):
        plt.scatter(X[:, 0], X[:, 1], c = y, cmap = cmap_bold)   # 绘制散点
    plt.show()

iris = datasets.load_iris() 　　　　　　　　　　　　　　　　　　　　　　# 数据集②
X1 = iris.data[:, 0:3:2]   　　　　　　　　　　　　　　　　　　　　　　 # 0:3:2 意思是，取所有行，取列中由0~3以2递增的索引值。
X2 = iris.data[:, 0:2]
X3 = iris.data[:, 1:3]
y = iris.target
knnDemo(X2, y, 15)

太长的备注放在这里八：

①   # xx1是伪造的数据，是第一行；xx2是伪造数据的第二行

      #     np.array([xx1.ravel(), xx2.ravel()]).T 是创造出来的待分类数据

      #        np.arange(start, end, step) 创建从start开始到end并且以step步伐递增的矩阵

      #        （n * m 变为 nm * 1 大小的矩阵，与flatten()相似，后者占据内存空间，而ravel()是视图）

 

②  # 鸢尾属植物数据集，该数据集包含了三种iris类型（Setosa、Versicolor 和 Virginica）的150个样本，每个样本具有4个特征，也即 iris.data 矩阵大小是 150 * 4

      # 特征分别是萼片宽度、萼片长度、花瓣长度和花瓣宽度，单位是cm。

 

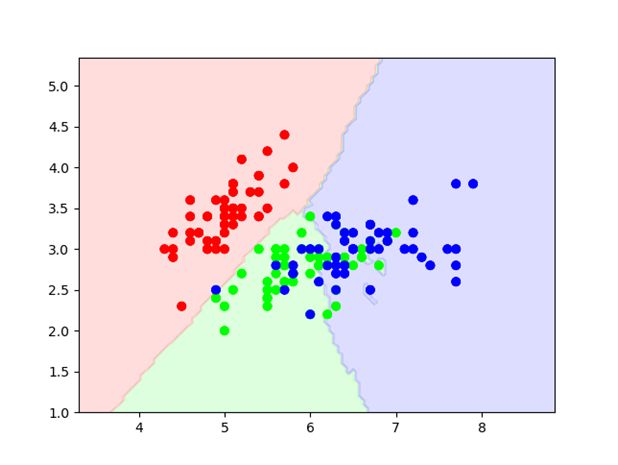
图1 3-Class classification(k=15, weight=’uniform’)

　　图像可见分类，红色、绿色、蓝色三个类别的花朵。后面懒得写了，自行感悟吧。

 

三、我的k-NN之感（k-NN优势与劣势）

优：

　　比较简单亲民？还有……可能某些方面的分类效果还是不错的？

劣：

　　数据收集这方面，就不多说了。首先，有些难以确定没想特征值对结果影响的比重（归一化感觉还是有些粗暴？）；其次，算待分类样本与已分类样本的差距，感觉这个很有拓展性；还有，如果得出多个标签出现次数相同的情况，可能还得进一步处理？

　　另外，矩阵运算量还蛮多的，如果每一次都要计算样本差值，求平方再开，遍历一次求最值，感觉代价有些大。

 

====================================  题外  ====================================

　　一开始没get到 .argsort() 的神奇作用，还写了快速排序，既然写了，那就贴吧：

 1 def QuickSort(array1):
 2     left = 0
 3     right = array1.shape[0] - 1
 4     pilot = array1[0]
 5     while left < right :
 6         while right != left and array1[right] > pilot :
 7             right -= 1
 8         array1[left] = array1[right]
 9         while left != right and array1[left] < pilot :
10             left += 1
11         array1[right] = array1[left]
12     array1[left] = pilot
13 
14     count = array1.shape[0]
15     if left > 1 :
16         array2 = array1[0 : left]
17         array1[0 : left] = QuickSort(array2)
18     if right < count - 2:
19         array3 = array1[right + 1 : count]
20         array1[right + 1 : count] = QuickSort(array3)
21     return array1

View Code

　　写到后来我也觉得莫名的，感觉不太“好看”，语法不熟悉？于是search，我是有空间性能上的一点点优势吧，但感觉可读性没这么好。

==================================  结束题外  ==================================

 

立Flag：下一波应该是关于回归。

 

参考书目：

-       机器学习系统设计 David Julian

-       机器学习实战 Perter Harrington