一:学习总结:
(一)查找的基本概念:
查找(Searching)就是根据给定的某个值,在查找表中确定一个其关键字等于给定值得数据元素(或记录)。
查找表(Search Table)是同一类型的数据元素(或记录)构成的集合。
查找表按照操作方式分为两大类:
静态查找表:只作查找操作的查找表。
顺序表查找、有序表查找、线性索引查找
动态查找表:在查找过程中同时插入查找表中不存在的数据元素,或者从查找表中删除已经存在的某个元素。
二叉排序树、平衡二叉树(AVL树)、多路查找树(B树)
(二)顺序表的查找:
这是最简单的一种,从表中的最后一个记录开始,逐个进行记录的关键字与给定值进行比较,若某个记录的关键字与给定值相等,则查找成功,找到所查的记录;反之,若直到第一个记录,其关键字和给定值比较都不相等,则表明表中没有所查的记录,查找失败。
平均的查找长度为(n+1)/2,最好的长度为1,最差的查找长度为n。时间复杂度o(n)
优化措施:
设置哨兵
设置a[0] 为关键字值,称之为哨兵,当返回值为0则表示未找到。从尾部开始查找。
免去了查找过程中每一次比较后都要判断查找位置是否越界的小技巧。
将查找概率大的记录放到查找表的前面。
(三)有序表的查找:
折半查找(二分法查找)
平均查找长度:log(n+1)-1,通过二分查找树的判断树来推的。二分查找的最坏性能和平均性能非常接近。时间复杂度o(lgn)。
插值查找
这种方法是在二分查找基础上改进的,核心是对mid的取值,公式为:
mid = low + (key - arr[low])*(high-low)/(arr[high]-arr[low])
至于为什么这么改进,因为key小的话,那么我趋向于在表中低地址端去查找,而key大的话那么我们趋向在表的高地址端去查找。
时间复杂度也是 o(lgn)。
斐波那契查找
不是采用二分,而是斐波拉契序列的值去缩小我们的范围。时间复杂度o(lgn)。
(四)平衡查找树: 由于二叉排序树一般都不是平衡的,而二叉排序树的查找性能取决于二叉排序树的形状,所以构造一种平衡的二叉树。左右子树高度相差不到1。所以此树总是平衡的。提高了查找效率。
二叉树上的结点的左子树的深度减去右子树的深度的值称为平衡因子BF。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。
平衡二叉树的构建过程:
总之就是把不平衡消灭在最早的时刻。
查找时间复杂度为O(logn),而插入和删除的时间复杂度也为O(logn)。
红黑树,二叉排序树的另外一种平衡算法。
(五)多路查找树:
目的:为了降低对外存设备的访问次数。
定义:多路查找书,其每一个结点的孩子树可以多于两个,且每一个结点处可以存储多个元素。
堵路查找树的形式:
2-3树
2-3-4树
B树 平衡的多路查找树
B+树 为了解决所有元素遍历的问题
结点最大的孩子数目称为B树的阶,因此,2-3树是3阶B数。
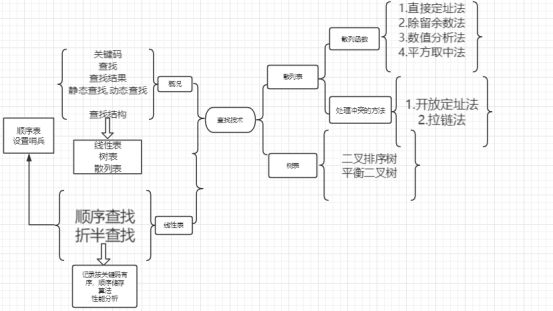
二:思维导图:
题目一:
1.题目名称:6-2 是否二叉搜索树
本题要求实现函数,判断给定二叉树是否二叉搜索树。
函数接口定义:
bool IsBST ( BinTree T );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
函数IsBST须判断给定的T是否二叉搜索树,即满足如下定义的二叉树:
定义:一个二叉搜索树是一棵二叉树,它可以为空。如果不为空,它将满足以下性质:
- 非空左子树的所有键值小于其根结点的键值。
- 非空右子树的所有键值大于其根结点的键值。
- 左、右子树都是二叉搜索树。
如果T是二叉搜索树,则函数返回true,否则返回false。
2.2 设计思路(伪代码或流程图)
1.空树是二叉排序树;
2.只有一个结点的树是二叉排序树;
3.左右子树都是二叉排序树,那这棵树是二叉排序树吗?再加一个条件就是啦——根节点大于左子树的最大值,并且小于右子树的最小值。
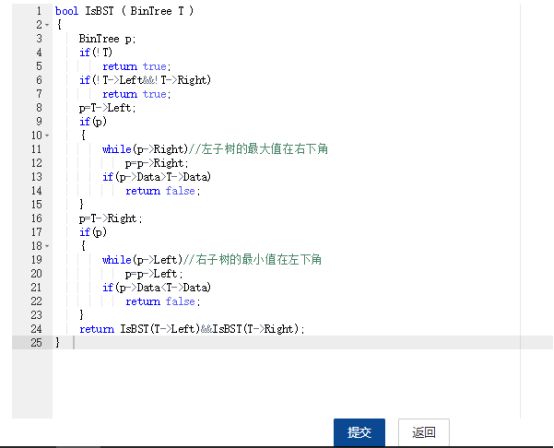
2.3 代码截图
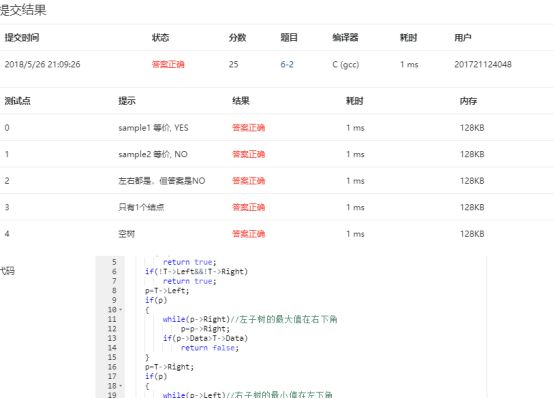
2.4 PTA提交列表说明
最开始没有考虑到T的条件问题,在 while(p->Right)//左子树的最大值在右下角的情况下没有实现p=T->Right,而是直接到判断p->Left的情况去;导致部分正确的结果;
题目二:
1.题目名称:6-3 二叉搜索树中的最近公共祖先(25 分)
在一棵树T中两个结点u和v的最近公共祖先(LCA),是树中以u和v为其后代的深度最大的那个结点。现给定某二叉搜索树(BST)中任意两个结点,要求你找出它们的最近公共祖先。
函数接口定义:
int LCA( Tree T, int u, int v );
其中Tree的定义如下:
typedef struct TreeNode *Tree;
struct TreeNode {
int Key;
Tree Left;
Tree Right;
};
函数LCA须返回树T中两个结点u和v的最近公共祖先结点的键值。若u或v不在树中,则应返回ERROR。
- 设计思路及流程图:
设计思路:有两种情况:一:u,v不在树中;
二:u,v在树中:(1)u,v都在左子树上面;
(2)u,v一个在左子树上面,一个在右子树上面;
(3)u,v有一个在根上面;
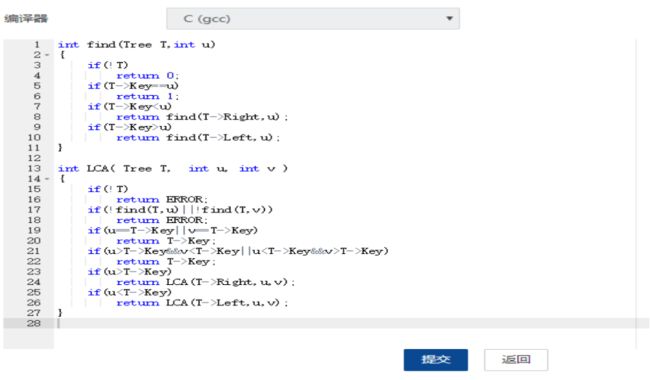
代码截图:
题目三:
1.题目名称:7-2 航空公司VIP客户查询
不少航空公司都会提供优惠的会员服务,当某顾客飞行里程累积达到一定数量后,可以使用里程积分直接兑换奖励机票或奖励升舱等服务。现给定某航空公司全体会员的飞行记录,要求实现根据身份证号码快速查询会员里程积分的功能。
输入格式:
输入首先给出两个正整数N(≤105)和K(≤500)。其中K是最低里程,即为照顾乘坐短程航班的会员,航空公司还会将航程低于K公里的航班也按K公里累积。随后N行,每行给出一条飞行记录。飞行记录的输入格式为:18位身份证号码(空格)飞行里程。其中身份证号码由17位数字加最后一位校验码组成,校验码的取值范围为0~9和x共11个符号;飞行里程单位为公里,是(0, 15 000]区间内的整数。然后给出一个正整数M(≤105),随后给出M行查询人的身份证号码。
输出格式:
对每个查询人,给出其当前的里程累积值。如果该人不是会员,则输出No Info。每个查询结果占一行
- 设计思路:
这是一道考察快速查找匹配的题目,可以使用哈希表的方法做,单较为繁琐。
设计思路:
int main()
{
char id[20];
定义变量tmp,n,m,k;
Scanf(输入身份照号;)
Hashlist H = Init(n);
for(LL i=0;i { 调用函数Insert(id,tmp,H); } scanf("%lld",&m); for(LL j=0;j { 调用函数 Find(id,H); if(f==NULL) printf("No Info\n"); else printf("%lld\n",f->miles); } }3.代码截图: 4.提交列表说明: 最开始调用函数不正确导致运行失误,然后编译器换成了c++才答案正确; 注意hash函数的选取,一开始我选取了后四位果断超时,选取了后五位即可AC,尽量让Hash函数取值接近数据最大值,这样能减少很多冲突。 请编写26个字母按特定字母值插入或删除的完整程序。 #include #include Typedef struct liuyu{char data;struct liuyu *link;} Liuyu *p,*q,*r,*head; Int L; //元素的个数 Int m=sizeof(test); Void build(); //主函数中被调用的函数应当预先说明; Void display(); //插入一个字母,在第Y字母之前,若无字母则加到末尾; int insert_char(char,char); //删除元素X,注意保存X的前驱元素指针; Int delet_char(char) Void build() //字母链表的生成; { Int i; Head=(test*)malloc(m); P=head; For(i=1;i { P->data=i+a-1; p->link=(test*)malloc(m); P=p->link;} Q->data=i+’a’-1; p->link=NULL; Void display()//字母链表的输出 { P=head; While(p->link!=NULL) { Printf(“%c”,p->data); P=p->link;} Printf(“%c”,p->data); Int insert_char(char X,char Y) //插入一个字母X在某个字母Y之前,若找不到字母Y则加到末尾; { P=head;r=(test*)malloc(m);r->data=X;if(head->data==Y) { Head=r;r->link=p;}else{while(p->data!=Y)&&(p->link!=NULL)){q=p;p=p->link; If(p->data==Y){q->link=r;r->link=p;} Else{p->link=r;r->link=NULL;} L++; Return 0; Int delet_char(char X)//删除X,保留X的前驱元素指针; { P=head; If(head->data==X){head=head->link:free(p);} Else{while(p->data!=X)&&(p->link!=NULL)) { q=p;p=link; {p=head; r=(test*)malloc(m); R->data=X; If(head->data=Y) { Head=r; S->link=p;} else{while((p->data!=Y)&&(p->link!=NULL)) { Q=p;p=p->link;} If(p->data==X){q->link=r;r->link=p;} Else{p->link=r;r->link=p}} L++; Return 0; } Int delet_char(char X)//删除元素X,保留X的前驱元素指针; { P=head; If(head->data==X){head=head->link;free(p):} Else{while(p->data!=X)&&(p->link!=NULL)) { Q=p; P->link;} Void main() //字母线性表的输入和输出; { L=26; Build(); Display(); Printf(“insert return value=%d\n”,insert_char(‘L’,‘W’)); Display(); Printf(“insert return value=%d\n”,delet_char(‘z’)); Display(); } 3.截图本周题目集的PTA最后排名