本文内容取自于小甲鱼的数据结构与算法。http://www.jianshu.com/p/230e6fde9c75
1. 线性表
线性表(List):由零个或多个数据元素组成的有限序列。
这里需要强调几个关键的地方:
首先它是一个序列,也就是说元素之间是有个先来后到的。若元素存在多个,则第一个元素无前驱,而最后一个元素无后继,其他元素都有且只有一个前驱和后继。另外,线性表强调是有限的,事实上无论计算机发展到多强大,它所处理的元素都是有限的。
若将线性表记为(a1,…,ai-1,ai,ai+1,…an),则表中ai-1领先于ai,ai领先于ai+1,称ai-1是ai的直接前驱元素,ai+1是ai的直接后继元素。
所以线性表元素的个数n(n>=0)定义为线性表的长度,当n=0时,称为空表。
1.1 线性表之数组
1.1.1 操作
(1) 定义线性表
线性表存储结构定义:
大家看到了,这里我们封装了一个结构,事实上就是对数组进行封装,增加了个当前长度的变量罢了。
总结下,顺序存储结构封装需要三个属性:
存储空间的起始位置,数组data,它的存储位置就是线性表存储空间的存储位置。
线性表的最大存储容量:数组的长度MaxSize。
线性表的当前长度:length。
注意,数组的长度与线性表的当前长度需要区分一下:
数组的长度是存放线性表的存储空间的总长度,一般初始化后不变。
而线性表的当前长度是线性表中元素的个数,是会变化的。
(2) 获取元素
实现GetElem的具体操作,即将线性表L中的第i个位置元素值返回。就程序而言非常简单了,我们只需要把数组第i-1下标的值返回即可。
(3) 插入元素
1. 如果插入位置不合理,抛出异常;
2. 如果线性表长度大于等于数组长度,则抛出异常或动态增加数组容量;
3. 从最后一个元素开始向前遍历到第i个位置,分别将它们都向后移动一个位置;
4. 将要插入元素填入位置i处;
5. 线性表长+1。
(4) 删除元素
1. 如果删除位置不合理,抛出异常;
2. 取出删除元素;
3. 从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置;
4. 表长-1。
1.1.2 优缺点
线性表的顺序存储结构,在存、读数据时,不管是哪个位置,时间复杂度都是O(1)。而在插入或删除时,时间复杂度都是O(n)。这就说明,它比较适合元素个数比较稳定,不经常插入和删除元素,而更多的操作是存取数据的应用。
(1) 优点
无须为表示表中元素之间的逻辑关系而增加额外的存储空间。
可以快速地存取表中任意位置的元素。
(2) 缺点
插入和删除操作需要移动大量元素。
当线性表长度变化较大时,难以确定存储空间的容量。
容易造成存储空间的“碎片”。
1.2 线性表之链表
前面我们讲的线性表的顺序存储结构,它最大的缺点就是插入和删除时需要移动大量元素,这显然就需要耗费时间。那我们能不能针对这个缺陷或者说遗憾提出解决的方法呢?要解决这个问题,我们就得考虑一下导致这个问题的原因!为什么当插入和删除时,就要移动大量的元素?原因就在于相邻两元素的存储位置也具有邻居关系,它们在内存中的位置是紧挨着的,中间没有间隙,当然就无法快速插入和删除。
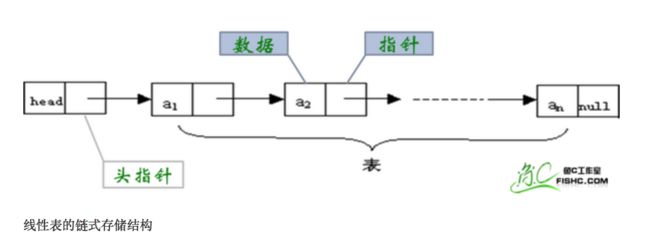
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素,这组存储单元可以存在内存中未被占用的任意位置。比起顺序存储结构每个数据元素只需要存储一个位置就可以了。
1.2.1 单链表
现在链式存储结构中,除了要存储数据元素信息外,还要存储它的后继元素的存储地址(指针)。也就是说除了存储其本身的信息外,还需存储一个指示其直接后继的存储位置的信息。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。这两部分信息组成数据元素称为存储映像,称为结点(Node)。n个结点链接成一个链表,即为线性表(a1, a2, a3, …, an)的链式存储结构。因为此链表的每个结点中只包含一个指针域,所以叫做单链表。
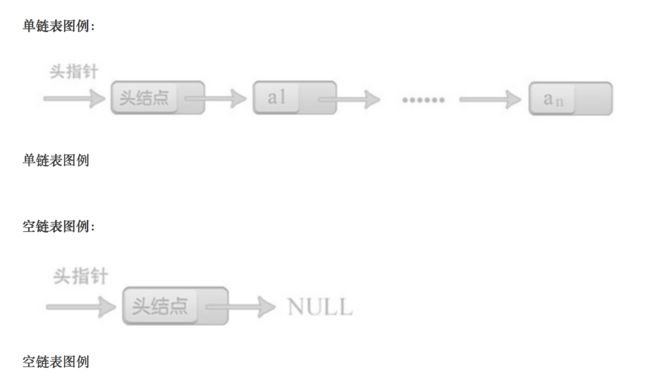
对于线性表来说,总得有个头有个尾,链表也不例外。我们把链表中的第一个结点的存储位置叫做头指针,最后一个结点指针为空(NULL)。
头指针:
1. 头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针。
2. 头指针具有标识作用,所以常用头指针冠以链表的名字(指针变量的名字)。
3. 无论链表是否为空,头指针均不为空。
4. 头指针是链表的必要元素。
头结点:
1. 头结点是为了操作的统一和方便而设立的,放在第一个元素的结点之前,其数据域一般无意义(但也可以用来存放链表的长度)。
2. 有了头结点,对在第一元素结点前插入结点和删除第一结点起操作与其它结点的操作就统一了。
3. 头结点不一定是链表的必须要素。
1.2.1.1 操作
(1) 定义单链表
我们看到结点由存放数据元素的数据域和存放后继结点地址的指针域组成。假设p是指向线性表第i个元素的指针,则该结点ai的数据域我们可以用p->data的值是一个数据元素。结点ai的指针域可以用p->next来表示,p->next的值是一个指针。那么p->next指向谁呢?当然指向第i+1个元素!也就是指向ai+1的指针。
问题:如果p->data = ai,那么p->next->data = ?
答案:p->next->data = ai+1。
(2) 读取元素
在线性表的顺序存储结构中,我们要计算任意一个元素的存储位置是很容易的。但在单链表中,由于第i个元素到底在哪?我们压根儿没办法一开始就知道,必须得从第一个结点开始挨个儿找。因此,对于单链表实现获取第i个元素的数据的操作GetElem,在算法上相对要麻烦一些。
1. 声明一个结点p指向链表第一个结点,初始化j从1开始;
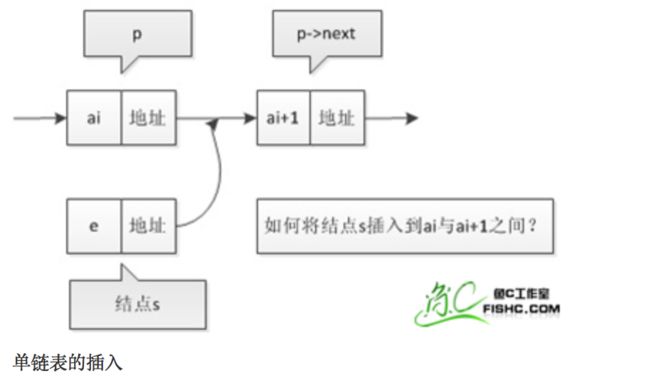
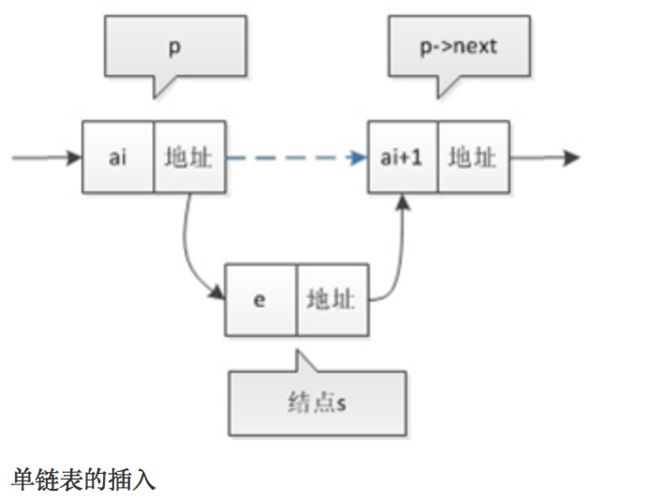
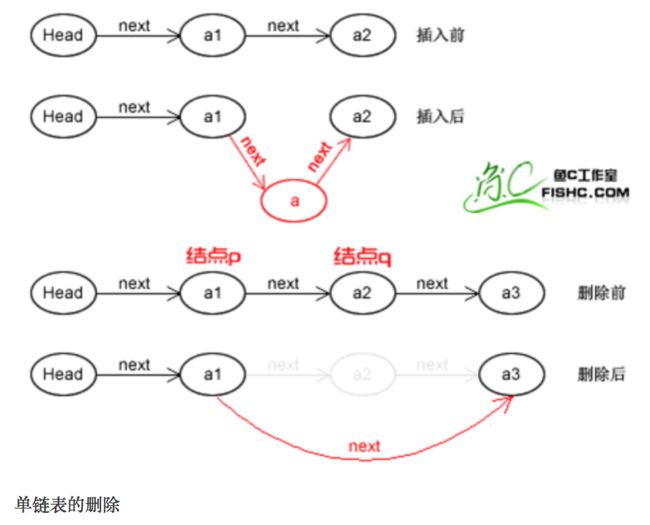
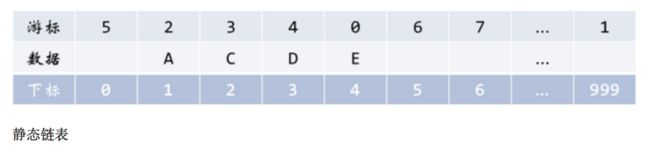
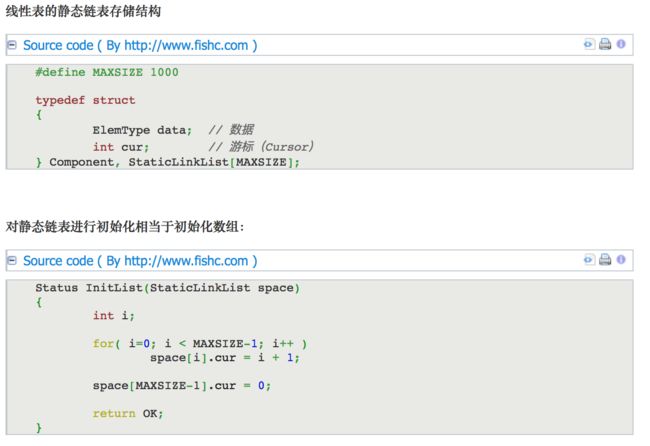
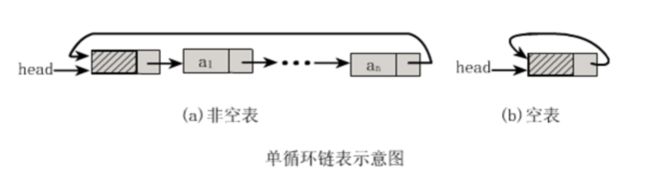
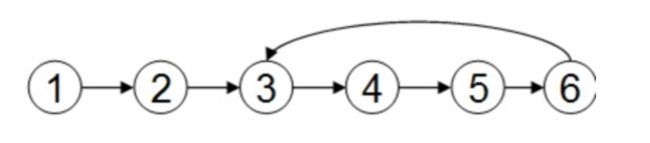
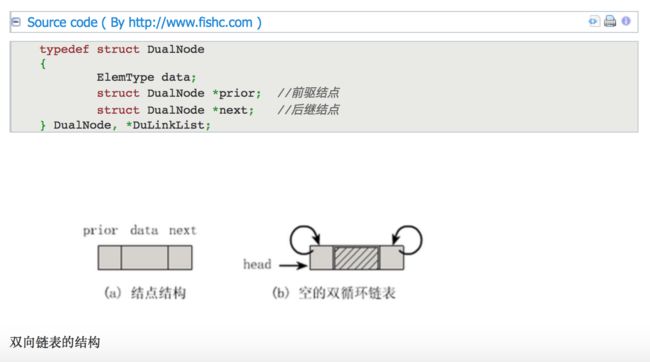
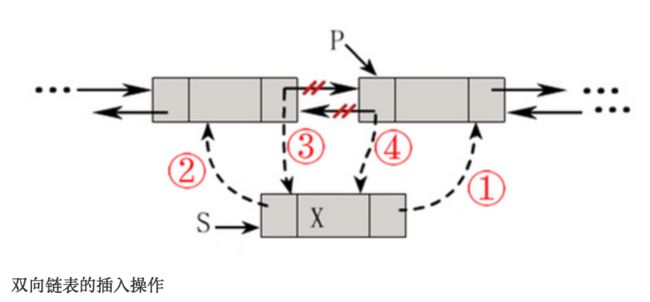
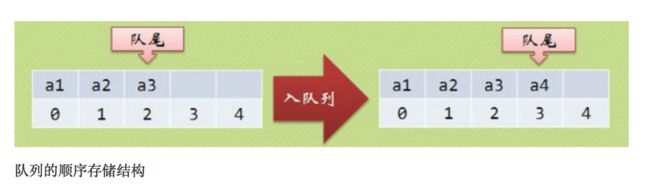
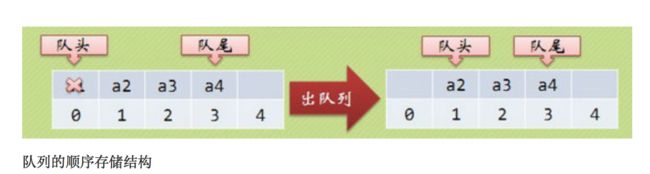
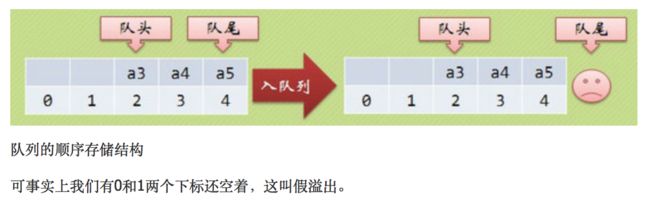
2. 当j 3. 若到链表末尾p为空,则说明第i个元素不存在; 4. 否则查找成功,返回结点p的数据。 (3) 插入元素 我们先来看下单链表的插入。假设存储元素e的结点为s,要实现结点p、p->next和s之间逻辑关系的变化,大家参考下图思考一下: 我们思考后发觉根本用不着惊动其他结点,只需要让s->next和p->next的指针做一点改变。 s->next = p->next; p->next = s; 我们通过图片来解读一下这两句代码。 那么我们考虑一下大部分初学者最容易搞坏脑子的问题:这两句代码的顺序可不可以交换过来?先 p->next = s;再 s->next = p->next; 大家发现没有?如果先执行p->next的话会先被覆盖为s的地址,那么s->next = p->next其实就等于s->next = s了。所以这两句是无论如何不能弄反的,这点初学者一定要注意咯~ 思路: 1. 声明一结点p指向链表头结点,初始化j从1开始; 2. 当j<1时,就遍历链表,让p的指针向后移动,不断指向下一结点,j累加1; 3. 若到链表末尾p为空,则说明第i个元素不存在; 4. 否则查找成功,在系统中生成一个空结点s; 5. 将数据元素e赋值给s->data; 6. 单链表的插入刚才两个标准语句; 7. 返回成功。 (4) 删除元素 现在我们再来看单链表的删除操作。 假设元素a2的结点为q,要实现结点q删除单链表的操作,其实就是将它的前继结点的指针绕过指向后继结点即可。那我们所要做的,实际上就是一步: 可以这样:p->next = p->next->next; 也可以是:q=p->next; p->next=q->next。 思路: 1. 声明结点p指向链表第一个结点,初始化j=1; 2. 当j<1时,就遍历链表,让P的指针向后移动,不断指向下一个结点,j累加1; 3. 若到链表末尾p为空,则说明第i个元素不存在; 4. 否则查找成功,将欲删除结点p->next赋值给q; 5. 单链表的删除标准语句p->next = q->next; 6. 将q结点中的数据赋值给e,作为返回; 7. 释放q结点。 对于顺序存储结构的线性表的整表创建,我们可以用数组的初始化来直观理解。 而单链表和顺序存储结构就不一样了,它不像顺序存储结构数据这么集中,它的数据可以是分散在内存各个角落的,他的增长也是动态的。对于每个链表来说,它所占用空间的大小和位置是不需要预先分配划定的,可以根据系统的情况和实际的需求即时生成。 创建单链表的过程是一个动态生成链表的过程,从“空表”的初始状态起,依次建立各元素结点并逐个插入链表。 思路: 1. 声明一结点p和计数器变量i; 2. 初始化一空链表L; 3. 让L的头结点的指针指向NULL,即建立一个带头结点的单链表; 4. 循环实现后继结点的赋值和插入。 (1) 头插法建立 头插法从一个空表开始,生成新结点,读取数据存放到新结点的数据域中,然后将新结点插入到当前链表的表头上,直到结束为止。简单来说,就是把新加进的元素放在表头后的第一个位置:先让新节点的next指向头节点之后,然后让表头的next指向新节点。 (2) 尾插法建立 头插法建立链表虽然算法简单,但生成的链表中结点的次序和输入的顺序相反。就像现实社会我们鄙视插队不遵守纪律的孩子,那编程中我们也可以不这么干,我们可以把思维逆过来:把新结点都插入到最后,这种算法称之为尾插法。 当我们不打算使用这个单链表时,我们需要把它销毁(真狠,不要就给别人嘛,还销毁~)。 其实也就是在内存中将它释放掉,以便于留出空间给其他程序或软件使用。 思路: 1. 声明结点p和q; 2. 将第一个结点赋值给p,下一结点赋值给q; 3. 循环执行释放p和将q赋值给p的操作; 这段算法代码里,常见的错误就是有同学会觉得q变量没有存在的必要,只需要在循环体内直接写free(p); p = p->next; 即可? 可这个世上没有无缘无故的爱,这样做会带来什么问题呢? 要知道p是一个结点,它除了有数据域,还有指针域。当我们做free(p);时候,其实是对它整个结点进行删除和内存释放的工作。而我们整表删除 是需要一个个结点删除的,所以我们就需要q来记载p的下一个结点。 我们分别从存储分配方式、时间性能、空间性能三方面来做对比。 (1) 存储分配方式 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素。 单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素。 (2) 时间性能 查找: 顺序存储结构O(1), 单链表O(n) 插入和删除: 顺序存储结构需要平均移动表长一半的元素,时间为O(n) 单链表在计算出某位置的指针后,插入和删除时间仅为O(1) (3) 空间性能 顺序存储结构需要预分配存储空间,分大了,容易造成空间浪费,分小了,容易发生溢出。 单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制。 总而言之, 若线性表需要频繁查找,很少进行插入和删除操作时,宜采用顺序存储结构。 若需要频繁插入和删除时,宜采用单链表结构。 比如说游戏开发中,对于用户注册的个人信息,除了注册时插入数据外,绝大多数情况都是读取,所以应该考虑用顺序存储结构。 而游戏中的玩家的武器或者装备列表,随着玩家的游戏过程中,可能会随时增加或删除,此时再用顺序存储就不太合适了,单链表结构就可以大展拳脚了。 当线性表中的元素个数变化较大或者根本不知道有多大时,最好用单链表结构,这样可以不需要考虑存储空间的大小问题。 而如果事先知道线性表的大致长度,比如一年12个月,一周就是星期一至星期日共七天,这种用顺序存储结构效率会高很多。 用数组描述的链表叫做静态链表,这种描述方法叫做游标实现法。 我们对数组的第一个和最后一个元素做特殊处理,他们的data不存放数据。我们通常把未使用的数组元素称为备用链表。数组的第一个元素,即下标为0的那个元素的cur就存放备用链表的第一个结点的下标。数组的最后一个元素,即下标为MAXSIZE-1的cur则存放第一个有数值的元素的下标,相当于单链表中的头结点作用。 回收空闲游标。 优点: 在插入和删除操作时,只需要修改游标,不需要移动元素,从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点。 缺点: 没有解决连续存储分配(数组)带来的表长难以确定的问题。 失去了顺序存储结构随机存取的特性。 总的来说,静态链表其实是为了给没有指针的编程语言设计的一种实现单链表功能的方法。 尽管我们可以用单链表就不用静态链表了,但这样的思考方式是非常巧妙的,应该理解其思想,以备不时之需。 题目:快速找到未知长度单链表的中间节点。 既然是面试题就一定有普通方法和高级方法。 普通的方法很简单,首先遍历一遍单链表以确定单链表的长度L。然后再次从头节点出发循环L/2次找到单链表的中间节点。 算法复杂度为:O(L+L/2)=O(3L/2)。 高级的方法:利用快慢指针! 利用快慢指针原理:设置两个指针*search、*mid都指向单链表的头节点。其中* search的移动速度是*mid的2倍。当*search指向末尾节点的时候,mid正好就在中间了。这也是标尺的思想。 对于单链表,由于每个结点只存储了向后的指针,到了尾部标识就停止了向后链的操作。也就是说,按照这样的方式,只能索引后继结点不能索引前驱结点。这会带来什么问题呢?例如不从头结点出发,就无法访问到全部结点。 事实上要解决这个问题也并不麻烦,只需要将单链表中终端结点的指针端由空指针改为指向头结点,问题就结了。将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表成为单循环链表,简称循环链表。 注:这里并不是说循环链表一定要有头结点。 其实循环链表的单链表的主要差异就在于循环的判断空链表的条件上,原来判断head->next是否为null,现在则是head->next是否等于head。回到刚才的问题,由于终端结点用尾指针rear指示,则查找终端结点是O(1),而开始结点是rear->next->next,当然也是O(1)。 有环的定义是,链表的尾节点指向了链表中的某个节点。 那么要判断单链表中是否有环,主要有以下两种方法: 方法一:使用p、q两个指针,p总是向前走,但q每次都从头开始走,对于每个节点,看p走的步数是否和q一样。如图,当p从6走到3时,用了6步,此时若q从head出发,则只需两步就到3,因而步数不等,出现矛盾,存在环。 方法二:使用p、q两个指针,p每次向前走一步,q每次向前走两步,若在某个时候p == q,则存在环。 大家都知道,任何事物出现的初期都显得有些不完善。例如我们的火车刚发明的时候是只有一个“头”的,所以如果它走的线路是如下: A->B->C->D->E->F->G->H->I->J->K->L->A 假设这会儿火车正停在K处呢,要他送一批货到J处,那么它将走的路线是: K->L->A->B->C->D->E->F->G->H->I->J 嗯,所以后来我们的火车就都有两个头了。看完这个例子,大家就明白双向链表的必要性了吧。 官方定义:栈(Stack)是一个后进先出(Last in first out,LIFO)的线性表,它要求只在表尾进行删除和插入操作。 小甲鱼定义:所谓的栈,其实也就是一个特殊的线性表(顺序表、链表),但是它在操作上有一些特殊的要求和限制:栈的元素必须“后进先出”。栈的操作只能在这个线性表的表尾进行。 注:对于栈来说,这个表尾称为栈的栈顶(top),相应的表头称为栈底(bottom)。 栈的插入操作(Push),叫做进栈,也称为压栈,入栈。类似子弹放入弹夹的动作。 栈的删除操作(Pop),叫做出栈,也称为弹栈。如同弹夹中的子弹出夹。 因为栈的本质是一个线性表,线性表有两种存储形式,那么栈也有分为栈的顺序存储结构和栈的链式存储结构。最开始栈中不含有任何数据,叫做空栈,此时栈顶就是栈底。然后数据从栈顶进入,栈顶栈底分离,整个栈的当前容量变大。数据出栈时从栈顶弹出,栈顶下移,整个栈的当前容量变小。 入栈操作: 入栈操作又叫压栈操作,就是向栈中存放数据。 入栈操作要在栈顶进行,每次向栈中压入一个数据,top指针就要+1,知道栈满为止。 出栈操作: 出栈操作就是在栈顶取出数据,栈顶指针随之下移的操作。 每当从栈内弹出一个数据,栈的当前容量就-1。 所谓清空一个栈,就是将栈中的元素全部作废,但栈本身物理空间并不发生改变(不是销毁)。因此我们只要将s->top的内容赋值为s->base即可,这样s->base等于s->top,也就表明这个栈是空的了。这个原理跟高级格式化一样只是但单纯地清空文件列表而没有覆盖硬盘的原理是一样的。 销毁一个栈与清空一个栈不同,销毁一个栈是要释放掉该栈所占据的物理内存空间,因此不要把销毁一个栈与清空一个栈这两种操作混淆。 计算栈的当前容量也就是计算栈中元素的个数,因此只要返回s.top-s.base即可。 注意,栈的最大容量是指该栈占据内存空间的大小,其值是s.stackSize,它与栈的当前容量不是一个概念哦。 现在我们来看下栈的链式存储结构,简称栈链。(通常我们用的都是栈的顺序存储结构存储,链式存储我们作为一个知识点,大家知道就好!) 栈因为只是栈顶来做插入和删除操作,所以比较好的方法就是将栈顶放在单链表的头部,栈顶指针和单链表的头指针合二为一。 队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。 与栈相反,队列是一种先进先出(First In First Out, FIFO)的线性表。 与栈相同的是,队列也是一种重要的线性结构,实现一个队列同样需要顺序表或链表作为基础。 队列既可以用链表实现,也可以用顺序表实现。跟栈相反的是,栈一般我们用顺序表来实现,而队列我们常用链表来实现,简称为链队列。 我们将队头指针指向链队列的头结点,而队尾指针指向终端结点。(注:头结点不是必要的,但为了方便操作,我们加上了。) 空队列时,front和rear都指向头结点。 出队列操作是将队列中的第一个元素移出,队头指针不发生改变,改变头结点的next指针即可。出队列的操作过程如下: 如果原队列只有一个元素,那么我们就应该处理一下队尾指针。 由于链队列建立在内存的动态区,因此当一个队列不再有用时应当把它及时销毁掉,以免过多地占用内存空间。 我们先按照应有的思路来考虑下如何构造队列的顺序存储结构,然后发掘都遇到了什么麻烦。 我们假设一个队列有n个元素,则顺序存储的队列需建立一个大于n的存储单元,并把队列的所有元素存储在数组的前n个单元,数组下标为0的一端则是队头。 入队列操作其实就是在队尾追加一个元素,不需要任何移动,时间复杂度为O(1)。 出队列则不同,因为我们已经架设下标为0的位置是队列的队头,因此每次出队列操作所有元素都要向前移动。 在现实中也是如此,一群人在排队买火车票,前边的人买好了离开,后面的人就要全部向前一步补上空位。可是我们研究数据结构和算法的一个根本目的就是要想方设法提高我们的程序的效率,按刚才的方式,出队列的时间复杂度是O(n),效率大打折扣! 如果我们不去限制队头一定要在下标为0的位置,那么出队列的操作就不需要移动全体元素。 但是这样也会出现一些问题,例如按下边的情形继续入队列,就会出现数组越界的错误。 要解决假溢出的办法就是如果后面满了,就再从头开始,也就是头尾相接的循环。 循环队列它的容量是固定的,并且它的队头和队尾指针都可以随着元素入出队列而发生改变,这样循环队列逻辑上就好像是一个环形存储空间。但要注意的是,在实际的内存当中,不可能有真正的环形存储区,我们只是用顺序表模拟出来的逻辑上的循环。 于是我们发觉了,似乎循环队列的实现只需要灵活改变front和rear指针即可。 也就是让front或rear指针不断加1,即时超出了地址范围,也会自动从头开始。我们可以采取取模运算处理: (rear+1) % QueueSize (front+1) % QueueSize 取模就是取余数的意思,他取到的值永远不会大于除数。1.2.1.2 单链表的整表建立
1.2.1.3 单链表的整表删除
1.2.1.4 优缺点
1.2.2 静态链表
1.2.2.1 定义静态链表
1.2.2.2 插入
1.2.2.3 删除
1.2.2.4 优缺点
1.2.2.5 单链表面试题
1.2.3 循环链表
1.2.3 带环单链表
1.2.4 双向链表
1.2.4.1 建立双向链表
1.2.4.2 插入
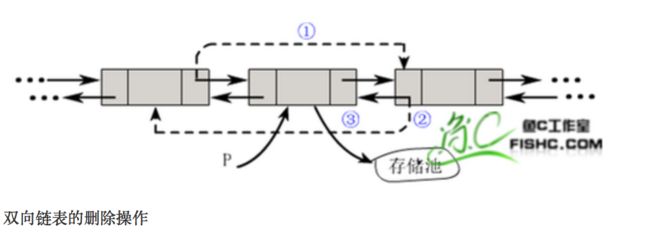
1.2.4.3 删除
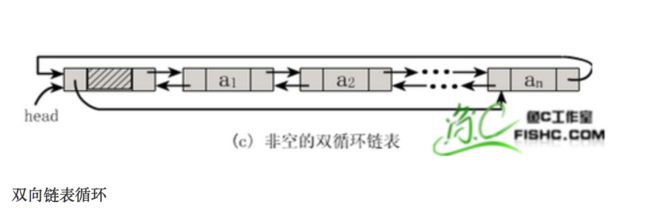
1.2.4 双向循环链表
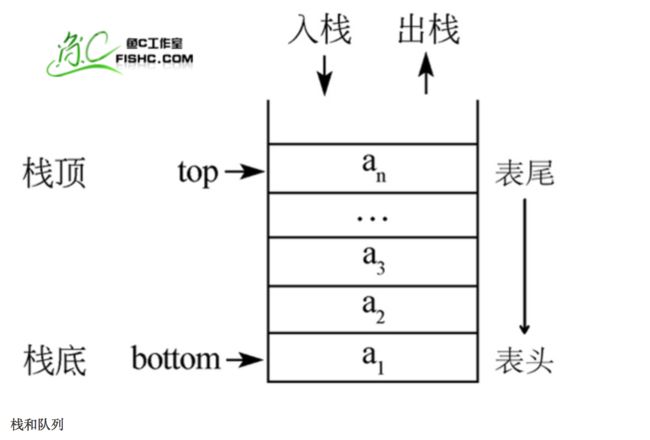
2. 栈
2.1 栈的顺序存储结构
2.1.1 清空栈
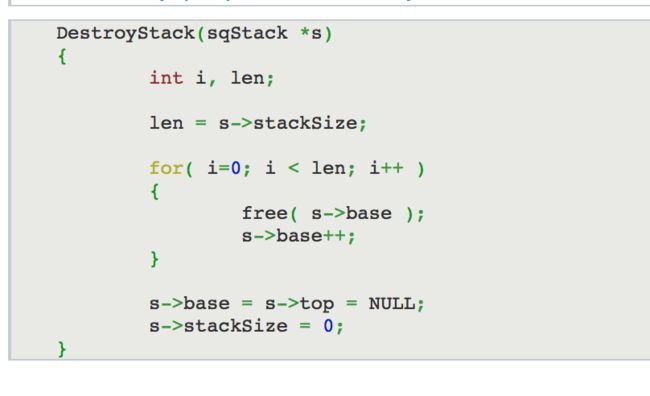
2.1.2 销毁栈
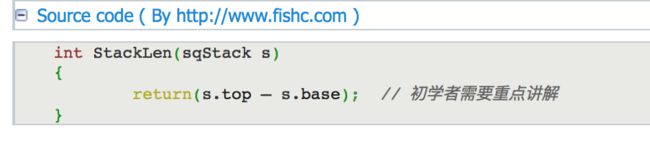
2.1.3 计算栈的当前容量
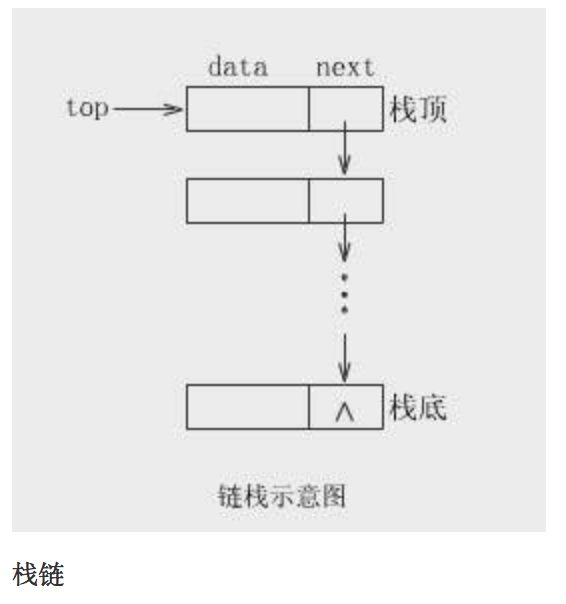
2.2 栈的链式存储结构
2.2.1 建立栈
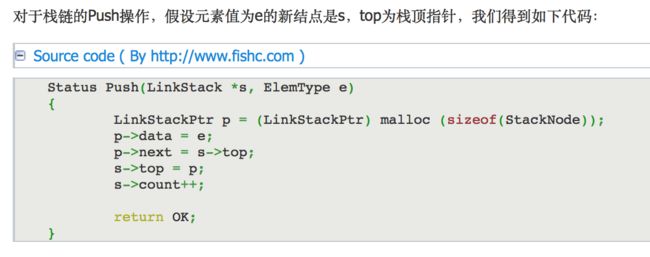
2.2.2 进栈
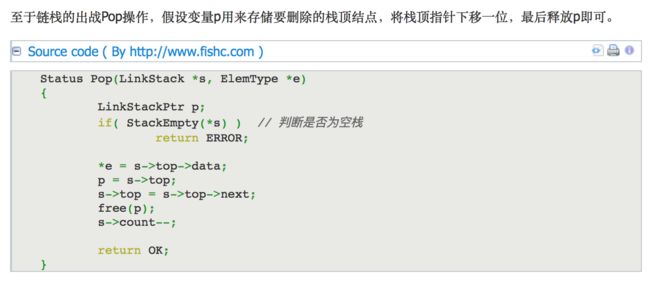
2.2.3 出栈
3. 队列
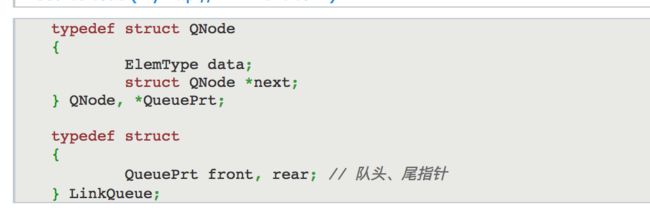
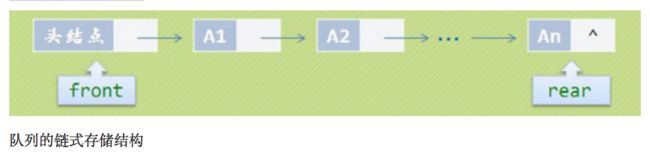
3.1 队列的链式存储结构
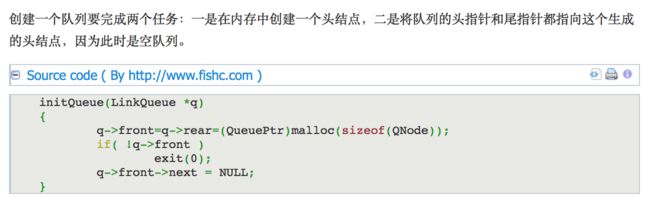
3.1.1 建立队列
3.1.2 入队列
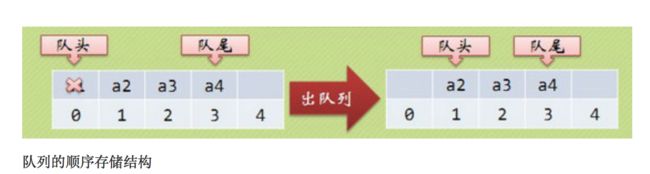
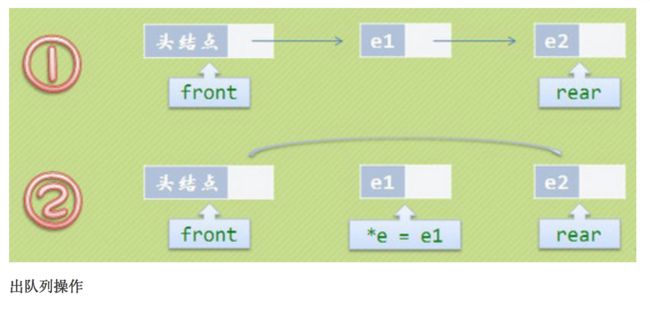
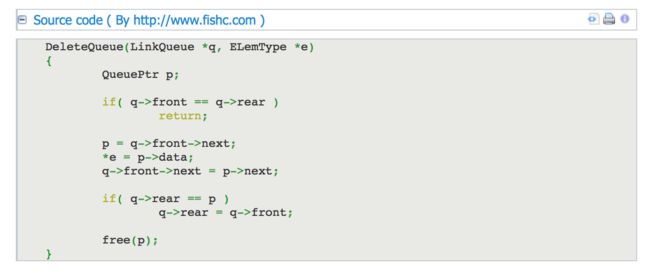
3.1.3 出队列
3.1.4 销毁队列
3.2 队列的顺序存储结构
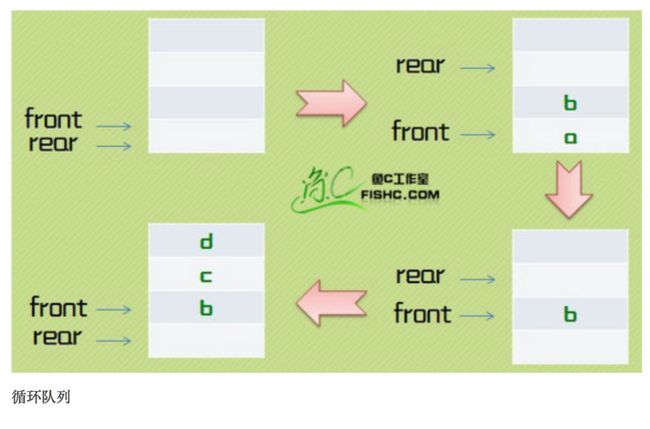
3.2.1 循环队列
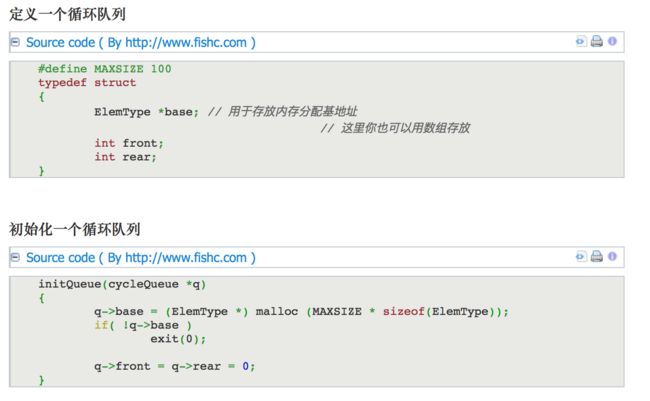
3.2.1.1 定义循环队列
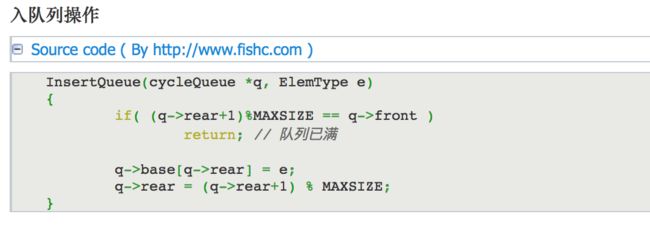
3.2.1.2 入队列
3.2.1.3 出队列