贝叶斯定理-执行数据分析解决肇事逃逸之谜
在这一章中,我们将:
- 应用著名的贝叶斯定理来解决计算机科学中的一个非常著名的问题。
- 向您展示如何使用贝叶斯定理和朴素贝叶斯来绘制数据,从真值表中发现异常值等等
贝叶斯定理概况
当我们使用贝叶斯定理的时候,我们是在测量一件事发生的概论程度:
上式表示在给定事件B的情况下事件A发生的概率。
概率通常被量化为0和1之间的一个数,包括这两者;0表示不可能,1表示绝对肯定。概率越大,确定性越大。掷骰子得到6的概率和掷硬币得到正面的概率这两个例子你们肯定很熟悉。还有另一个你们每天都熟悉和遇到的例子:垃圾邮件。
我们所有人通常一整天都在打开电子邮件(有些人甚至整夜都在打开!)伴随着我们所期待的信息,我们也将迎来那些我们不愿意、也不愿意接收的信息。我们都讨厌处理垃圾邮件。我每天收到的邮件中有一封是垃圾邮件的概率是多少?我关心它的内容的概率是多少?我们是怎么知道的?
让我们来谈谈垃圾邮件过滤器是如何工作的,因为,这可能是我们可以使用的关于概率的最好的例子!
大多数垃圾邮件过滤器的工作方式(至少在最基本的层次上)是定义一个单词列表,用于指示我们不想要或不要求接收的电子邮件。如果邮件中包含这些词,就会被认为是垃圾邮件.
从公式化的角度来看是这样的:
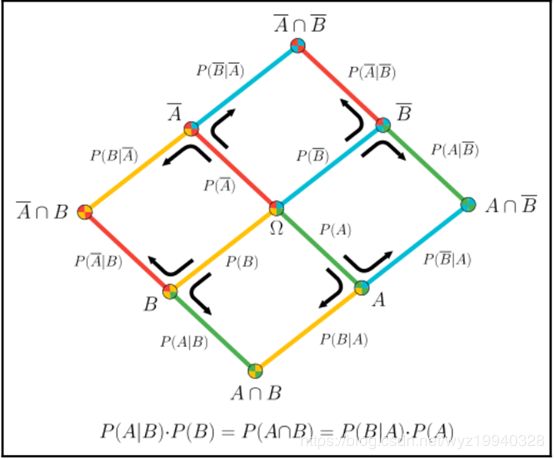
根据给定的一组单词,判断电子邮件是垃圾邮件的概率:维基百科中的用户Qniemiec有一个令人难以置信的可视化图表,该图表充分解释了概率视图的每个组合,该视图由两个事件树的叠加表示。这是一个完整的贝叶斯定理的可视化,它由两个事件树图的叠加表示:
现在,我们来看一个非常著名的问题。它有很多名字,但最基本的问题是所谓的出租车问题。这是我们的场景,我们将尝试用概率和贝叶斯定理来解决。
一名Uber司机卷入了一起肇事逃逸事故。著名的黄色出租车和Uber司机是在这个城市运营的两家公司,随处可见。我们得到以下数据:
- 该市85%的出租车是黄色的,15%是Uber。
- 一名目击者指认了肇事逃逸车辆的身份,并表示车上贴着Uber的贴纸。话虽如此,我们不知道证人的证词有多可靠,因此法院决定对用户进行测试并确定其可靠性。最终,法院得出结论,证人在80%的情况下正确识别了两辆车中的每一辆,但在20%的情况下未能识别。
这是很重要的,所以请注意接下来的内容:
我们的两难境地是:事故中涉及的车辆是Uber司机还是黄色出租车的概率是多少。
从数学上来说,以下就是我们如何得到我们需要的答案的过程:
- 正确识别的Uber司机总数为:
15*0.8=12
- 目击者有20%的时间是错误的,所以错误识别的车辆总数是:
85*0.2=17
- 因此,证人确认的车辆总数为12 + 17 = 29。因此,他正确识别Uber司机的概率是
12/29=41.3%
现在,让我们看看是否可以开发一个简单的程序来帮助我们得出这个数字,以证明我们的解决方案是可行的。为此,我们将深入研究我们的第一个开源工具包:Encog。Encog被设计用来处理这样的问题。
Encog框架是一个成熟的机器学习框架,由Jeff Heaton先生开发。希顿先生还出版了几本关于Encog框架以及其他主题的书籍,如果您打算广泛使用这个框架,我鼓励您去寻找它们。
让我们看看解决这个问题所需要的代码。你会注意到,数学,统计学,概率…这些都是从你那里抽象出来的。Encog可以让您专注于您试图解决的业务问题。
好,让我们把它分解成更容易消化的部分。我们要做的第一件事是创建一个贝叶斯网络。这个物体将是解开我们这个谜的核心。贝叶斯网络对象是概率和分类引擎的包装器。
贝叶斯网络由一个或多个贝叶斯事件组成。事件将是证据、结果或隐藏的三种不同类型之一,通常对应于训练数据中的一个数字。事件总是离散的,但是连续值(如果存在并且需要)可以映射到离散值的范围。
在创建初始网络对象之后,我们为Uber司机以及声称看到肇事逃逸司机的目击者创建一个事件。我们将在Uber司机和目击者之间建立一个依赖关系,然后确定我们网络的结构。
接下来,我们需要构建实际的真值表。真值表是一个函数可能具有的所有值的列表。有一行或多行复杂度不断增加,最后一行是最终的函数值。如果你还记得逻辑理论,基本上有三种操作可以使用:NOT, AND和OR。0通常表示false, 1通常表示true。
如果我们再深入一点,就会发现我们得到了下面的规则
If A = 0, -A = 1
If A = 1, -A = 0
A+B = 1, except when A and B = 0
A+B = 0 if A and B = 0
A*B = 0, except when A and B = 1
A*B = 1 if A and B = 1
现在,回到我们的代码。
为了构建真值表,我们需要知道概率和结果值。在我们的问题中,Uber司机卷入事故的可能性是85%。至于目击者,有80%的可能他们说的是真话,有20%的可能他们错了。我们将使用真值表的AddLine函数添加这些信息。
这是一个扩展真值表,显示了两个变量P和Q的所有可能真值函数。
如果我们要对真值表进行更广泛的编程,下面是一个例子:
a?.Table?.AddLine(0.5, true); // P(A) = 0.5
x1?.Table?.AddLine(0.2, true, true); // p(x1|a) = 0.2
x1?.Table?.AddLine(0.6, true, false);// p(x1|~a) = 0.6
x2?.Table?.AddLine(0.2, true, true); // p(x2|a) = 0.2
x2?.Table?.AddLine(0.6, true, false);// p(x2|~a) = 0.6
x3?.Table?.AddLine(0.2, true, true); // p(x3|a) = 0.2
x3?.Table?.AddLine(0.6, true, false);// p(x3|~a) = 0.6
现在我们的网络和真值表已经构建好了,是时候定义一些事件了。
如前所述,事件是证据、隐藏或结果的任何一种。隐藏的事件既不是证据也不是结果,但仍然与贝叶斯图本身有关。我们不会使用隐藏,但我想让你知道它确实存在。
要解开我们的谜团,我们必须积累证据。在我们的案例中,我们掌握的证据是,目击者报告称看到一名Uber司机参与了这起肇事逃逸事件。我们将定义一种事件类型的证据,并将其分配给证人报告的内容。如果结果,是一个优步司机,所以我们会给它分配一个事件类型的结果。
最后,我们必须承认,至少在某些时候,目击者看到一名优步司机卷入其中的报告是不正确的。因此,我们必须为目击者没有看到优步司机和优步司机没有参与的两种可能性创建事件值:
注意,我们将要执行的查询是EnumerationQuery。该对象允许对贝叶斯网络进行概率查询。这是通过计算隐藏节点的每个组合并使用总概率找到结果来实现的。如果贝叶斯网络很大,性能可能会很差,但幸运的是,它不是。
最后,我们对贝叶斯网络定义执行查询并打印结果,正如我们所希望的,是41.3%。
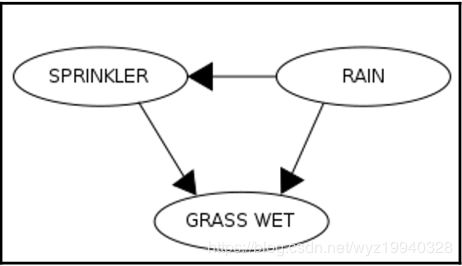
作为练习,看看现在是否可以使用Encog来解决另一个非常著名的示例。在这个例子中,我们早上醒来发现草是湿的。是下雨了,还是洒水器开着,还是两者都开了?这是我们的真值表在纸和笔上的样子:
下雨的概率:
完整真值表:
绘制数据
如前所述,朴素贝叶斯在解决复杂情况方面的效率惊人。虽然在某些情况下,它的性能肯定会优于其他算法,但它只是应用于您的问题的一个很好的初试算法。因为与许多其他模型相比,我们只需要非常少的训练数据。
在下一个应用程序中,我们将使用奇妙的Accord.NET机器学习框架,它为我们提供了一种工具,我们可以使用该工具输入数据、查看绘制的数据,并了解假阳性和假阴性。我们将能够为存在于数据空间中的对象输入数据,并将它们分类为绿色或蓝色。我们将能够改变这些数据,看看它们是如何分类的,更重要的是,它们是如何可视化表示的。我们的目标是了解新数据到达时属于哪组;它们不是绿色就是蓝色。此外,我们希望跟踪假阳性和假阴性。朴素贝叶斯会根据数据空间中的数据为我们做这些事。记住,在我们训练朴素贝叶斯分类器之后,最终目标是它能够从以前从未见过的数据中识别出新的对象。如果不能,那么我们需要回到训练阶段。
我们简单地讨论了真值表,现在是时候回过头来,在这个定义后面添加一些正式的东西了。更具体地说,我们用一个混淆矩阵来讨论。在机器学习中,混淆矩阵(错误矩阵或匹配矩阵)是一种表布局,可以让您可视化算法的性能。每一行表示预测的类实例,而每一列表示实际的类实例。它被称为混淆矩阵,因为可视化可以很容易地看出你是否混淆了两者。
真值表的抽象视图是这样的:
|
|
X 现在 (X present) |
X 缺省 (X absent) |
|
| 检测结果呈阳性 (Test positive) |
真阳性 (True positive) |
假阳性 (False positive) |
阳性总分 (Total positive) |
|
假阴性 (False negative) |
真阴性 (False negative) |
阴性总分 (Total negative) |
|
|
X发生的总分 (Total negative) |
X没发生的总分 (Total negative) |
总和 (Grand total) |
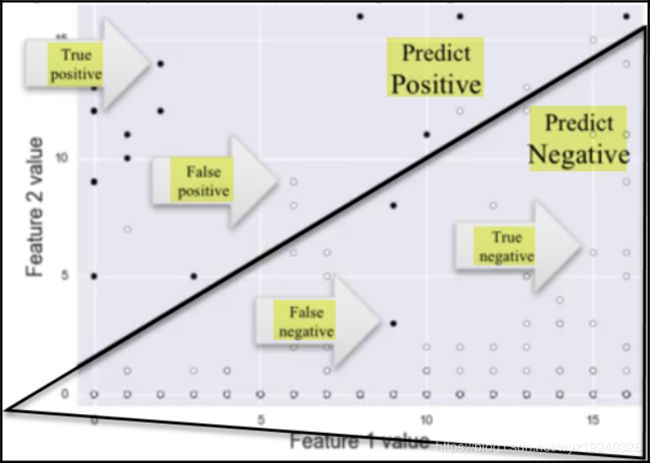
对同一个真值表的更直观的视图是这样的:
最后,对于一个真正的混淆矩阵有一个更正式的观点:
在机器学习领域,真值表/混淆矩阵允许您直观地评估算法的性能。正如您将在下面的应用程序中看到的,每当添加或更改数据时,您将能够看到是否出现了这些错误或负面条件。
目前,我们将要开始测试的数据在绿色和蓝色对象之间平均分配,所以在没有任何合理的可能性下,任何新的情况更有可能是其中一种或者另一种,而不是其他种。这种合理的概率,被称为先验概率。先验概率是基于我们对数据所见的先验经验,在很多情况下,这些信息被用来在结果发生之前预测结果。给定一个先验概率,我们就会得出一个结论,这个结论就成为我们的后验概率。
在我们的案例中:
- 绿色对象的先验概率是绿色对象的总数/数据空间中对象的总数
- 蓝色对象的先验概率等于蓝色对象的总数/数据空间中对象的总数
让我们进一步看看发生了什么。
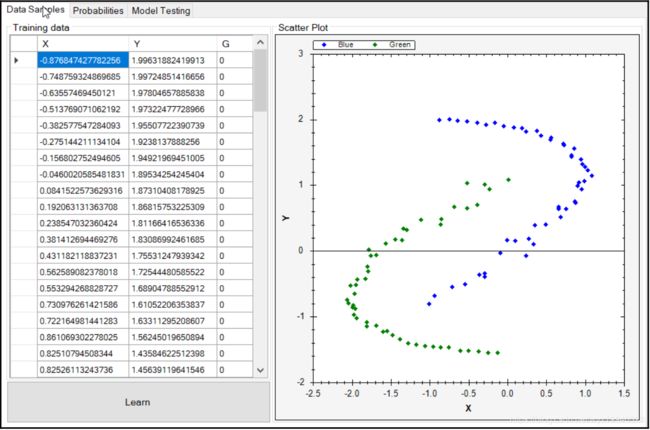
可以在下面的截图中看到我们的数据。X和Y列表示数据空间中沿着X和Y轴的坐标,G列是一个标签,表示对象是否为绿色。记住,监督学习应该给出我们想要达到的目标,朴素贝叶斯应该让我们很容易看出这是否正确。
如果我们使用前面的数据并创建它的散点图,它将看起来像下面的屏幕截图。如你所见,数据空间中的所有点都被绘制出来了,那些G列值为0的点被绘制成蓝色,而那些值为1的点被绘制成绿色。
每个数据点在数据空间中的X/Y位置上绘制,用X/Y轴表示:
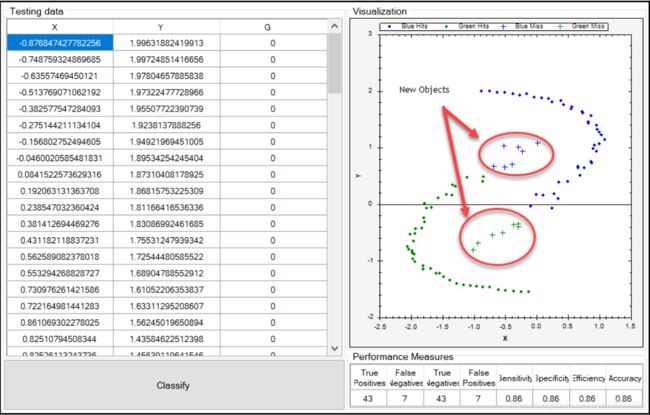
但是,当我们向数据空间添加新对象时,朴素贝叶斯分类器无法正确分类,会发生什么情况呢?我们最终得到了假阴性和假阳性,如下所示:
由于我们只有两类数据(绿色和蓝色),因此我们需要确定如何正确分类这些新数据对象。如您所见,我们有14个新的数据点,颜色编码显示它们与x轴和y轴的对齐位置。
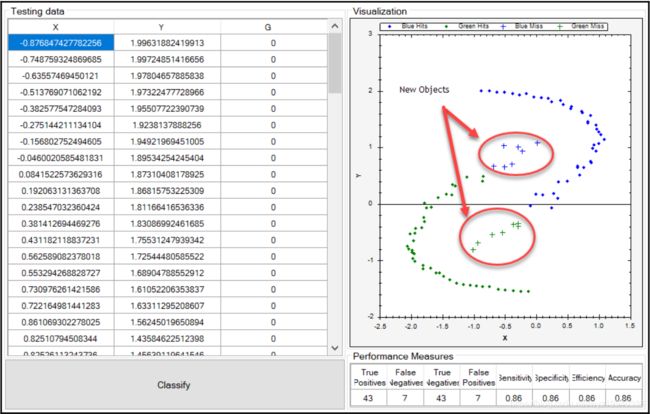
现在让我们以完整的形式查看应用程序。以下是我的主屏幕截图。在屏幕左侧的Data Samples选项卡下,我们可以看到已经加载了数据空间。在屏幕的右边,我们可以看到我们有一个散点图,它可以帮助我们可视化数据空间。如您所见,所有的数据点都被正确地绘制和着色了。
如果我们看看概率是如何分类和绘制的,你会发现数据几乎以两个封闭但重叠的簇的形式出现:
当空间中的一个数据点与另一个不同颜色的数据点重叠时,我们就需要朴素贝叶斯来完成它的工作。
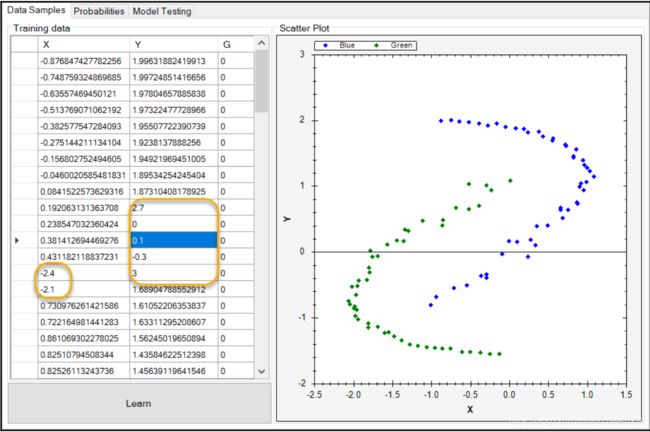
如果切换到模型测试选项卡,就可以看到添加的新数据点。
接下来,让我们修改已经添加的一些数据点,以显示任何一个数据点如何变为假阴性或假阳性。请注意,我们在开始这个练习时使用了7个假阴性和7个假阳性。
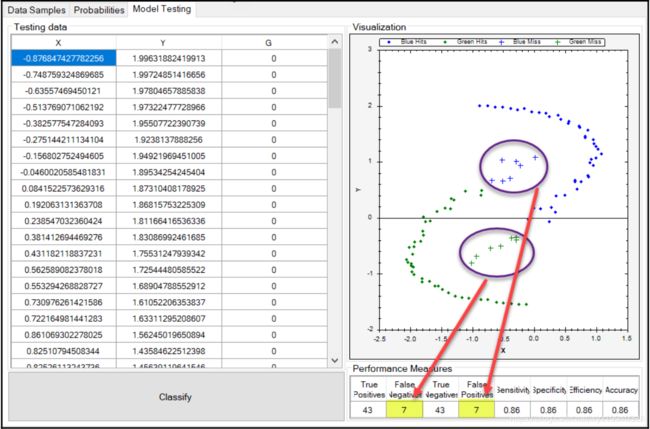
我们之前所做的数据修改结果如下图所示。如你所见,我们现在有额外的误报:
我将把数据的实验留给您,并继续您的朴素贝叶斯学习!
总结
在这一章中,我们学习了概率论,贝叶斯定理,朴素贝叶斯定理,以及如何将其应用于实际问题。我们还学习了如何开发一种工具来帮助我们测试分类器,并查看我们的数据是否包含任何假阴性或阳性。
在下一章中,我们将深入探讨机器学习的世界,并讨论强化学习。
转载请注明出处:https://www.cnblogs.com/wangzhenyao1994/p/10225616.html
文章发表的另一个地址:https://blog.csdn.net/wyz19940328/article/details/85863533