\(NOIP\)模拟题汇总(加厚版)
T1 string
描述
有一个仅由 '0' 和 '1' 组成的字符串 \(A\),可以对其执行下列两个操作:
- 删除 \(A\)中的第一个字符;
- 若 \(A\)中 '1' 出现的次数为奇数,则在 \(A\) 的末尾插入 '1',否则在 \(A\) 的末尾插入 '0'.
现在给出一个同样仅由 '0' 和 '1' 组成的字符串 \(B\),请你判断 \(A\) 能否在任意多次操作后转化为 \(B\)。
输入
输入文件第一行一个正整数 \(T\),表示有 \(T\) 组数据需要进行判断。
接下来依次输入 \(T\) 组数据,每组数据有两行,其中第一行包含一个字符串 \(A\),第二行包含一个字符串 \(B\)。
输出
输出共 \(T\) 行,对应 \(T\) 组询问。若第 \(i\) 组数据中 \(A\)串可以转化为 \(B\) 串则输出 "YES";否则输出 "NO"。
输入样例 1
2 01011 0110 0011 1110
输出样例 1
YES NO
提示
对于 \(20%\) 的数据,\(n\)≤\(10\), \(T\)=\(3\)
对于 \(50%\) 的数据,\(n\)≤\(1000\), \(T\)≤\(20\)。
对于 \(100%\) 的数据,\(n\)≤\(10^6\), \(T\)≤\(50\)。
题解
一道水题,但我考试的时候没想出来 。
自己手推几组样例,就会发现一个规律:ans只与01串中\(1\)的个数有关
因为你可以讲前面的数删掉加到后面形成组合;
所以如果\(A\)中\(1\)的个数大于等于\(B\)中\(1\)的个数则输出\(YES\),否则输出\(NO\);
但是要注意若\(A\)中\(1\)的个数为奇数要拿\((\)\(A\)中\(1\)的个数+1\()\)与\(B\)中\(1\)的个数比较即可;
code:
#include
#include
#include
#include
#include
#define ll long long
#define R register
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
char a[N],b[N];
int lena,lenb,A,B,t;
int main(){
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
read(t);
while(t--){
A=0;B=0;
scanf("%s%s",(a+1),(b+1));
lena=strlen(a+1);
lenb=strlen(b+1);
for(R int i=1;i<=lena;i++)
if(a[i]=='1')A++;
for(R int i=1;i<=lenb;i++)
if(b[i]=='1')B++;
if(A&1)A++;
if(A>=B)printf("YES\n");
else printf("NO\n");
}
return 0;
} T2 glide
描述
大森林中茂盛地生长着 \(N\) 棵树,从 \(1\) 到 \(N\) 编号,第 \(i\) 棵树的高度是 \(H_i\),住在这片森林里的飞鼠 Makik 可以在树与树之间滑翔。
有 \(M\) 组树能供 \(Makik\)在其间滑翔,在每组树间滑翔的时间是固定的。滑翔时,\(Makik\) 每秒会下落 \(1\) 米,即当 \(Makik\) 当前位置距离地面 \(h\) 米时,它经过 \(t\) 秒的滑翔后会落到距离地面 \(h-t\)米的高度上。但若\(h-t\) 小于 \(0\) 或比要到达的树高还要大,则 \(Makik\) 不能进行这次滑行。
除滑翔外,\(Makik\) 还可以沿着一棵树爬上爬下,每向上或向下移动 \(1\) 米均需花费 \(1\) 秒的时间。现在,\(Makik\) 想要从第 \(1\) 棵树上高度为 \(X\) 米的位置移动到第 \(N\) 棵树的顶端(高度为 \(H_N\) 的位置),请你帮它算一算最少要花费多少秒的时间。
输入
输入文件第一行包含三个整数 \(N\),\(M\),\(X\),分别表示树的数量、能供 \(Makik\) 在其间滑翔的树的组数和 \(Makik\) 的初始高度。
下面 \(N\) 行,其中第 \(i\) 行包含一个整数,表示第 \(i\) 棵树的高度 \(H_i\)。
接下来 \(M\) 行,其中 \(j\) 行包含三个整数 \(A_j\),\(B_j\),\(T_j\)(\(A_j\)\(\neq\) \(B_j\)),表示 \(Makik\) 可以在第 \(A_j\) 棵树和第 \(B_j\) 棵树间相互滑行,每次滑行的时间是 \(T_j\) 秒。数据保证每一组树都不会被多次给出。
输出
输出一行一个整数,表示 \(Makik\) 到达第 \(N\) 棵树所至少要花费的秒数。如果不能到达,输出 \(-1\)。
题解
我这道题在最短路上搞了一些操作,感觉想贪心,感觉不对,但是AC了;
输入样例 1
>5 5 0 >50 >100 >25 >30 >10 >1 2 10 >2 5 50 >2 4 20 >4 3 1 >5 4 20 >```
输出样例 1
110
提示
样例说明:
先沿第 \(1\) 棵树向上爬 \(50\) 米,再依次滑翔到第 \(2\) 棵、第 \(4\) 棵、第 \(5\) 棵树上,最后沿第 \(5\) 棵树向上爬 \(10\) 米。
数据规模与约定
对于 \(30\%\) 的数据,\(N\leq 1000\), \(M\leq 3000\), \(H_i\leq 100\), \(T_j\leq 100\)。
对于另外 \(30\%\) 的数据,\(X=0\)。
对于 \(100 \%\) 的数据,\(2\leq N\leq 100000\), \(1\leq M\leq 300000\), \(1\leq H_i\leq 10^9\), \(1\leq T_j\leq 10^9\), \(0\leq X\leq H_1\)。
题解
std讲的思路:
一直跑\(SPFA\)(或\(Dij\)堆优化),最后\(ans\)=(地底下的距离乘以2+地上的距离);
std’s code:
#include
using namespace std;
#define N 100005
#define M 600005
#define _inf -4557430888798830400ll
int n, m, h[N];
long long X, d[N];
priority_queue > q;
int head[N];
struct graph
{
int next, to, val;
graph() {}
graph(int _next, int _to, int _val)
: next(_next), to(_to), val(_val) {}
} edge[M];
inline void add(int x, int y, int z)
{
static int cnt = 0;
edge[++cnt] = graph(head[x], y, z);
head[x] = cnt;
}
void spfa(int s)
{
memset(d, 0xc0, sizeof d);
d[s] = X;
q.push(make_pair(X, s));
while (!q.empty())
{
int x = q.top().second; long long y = q.top().first; q.pop();
if (y != d[x]) continue;
for (int i = head[x]; i; i = edge[i].next)
if (edge[i].val <= h[x])
if (d[edge[i].to] < min(y - edge[i].val, 1ll * h[edge[i].to]))
d[edge[i].to] = min(y - edge[i].val, 1ll * h[edge[i].to]),
q.push(make_pair(d[edge[i].to], edge[i].to));
}
}
int main()
{
cin >> n >> m >> X;
for (int i = 1; i <= n; ++i)
scanf("%d", &h[i]);
for (int x, y, z, i = 1; i <= m; ++i)
scanf("%d%d%d", &x, &y, &z),
add(x, y, z), add(y, x, z);
spfa(1);
if (d[n] == _inf) cout << -1 << endl;
else cout << (X - d[n]) * 2 - X + h[n] << endl;
return 0;
} 我的思路:
老师的思路中细节比较少但可能不太好想,但我的写法比较好理解 \((*/ω\*)\)。
我的思路就是在\(SPFA\)中模拟一个\(H\)数组,\(H_i\)表示跑最短路时,在\(i\)点时的高度(就是你以最短路去走到\(i\)点时的高度)。
我认为就是在最短路时模拟......(细节比较多)
my code:
#include
#include
#include
#include
#include
#include
#define ll long long
#define R register
#define N 300005
#define INF 0x7fffffffffLL
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
int n,m,x,head[N],tot,flag,h[N],H[N],vis[N],u,v,w;
ll dist[N];
inline int abss(R int x){return x<0?-x:x;}
struct node{
int nex,to,dis;
}edge[N<<1];
inline void add(R int u,R int v,R int w){
edge[++tot].nex=head[u];
edge[tot].to=v;
edge[tot].dis=w;
head[u]=tot;
}
inline void spfa(R int s){
queueq;
for(R int i=1;i<=n;i++)dist[i]=INF;
q.push(s);vis[s]=1;dist[s]=0;H[s]=x;
while(!q.empty()){
R int x=q.front();q.pop();vis[x]=0;
for(R int i=head[x];i;i=edge[i].nex){
R int xx=edge[i].to;
//-------------下面是模拟判断 细节比较多-------------------------------------------------------
R int now=0;//now是模拟你需要爬多少步 正数为向上爬 负数为想下爬
if(H[x]-edge[i].dis<0)now=(edge[i].dis-H[x]);//以当前高度跳到要更新的点会跳到地下
else if(H[x]-edge[i].dis>h[xx])now=(-1)*(H[x]-edge[i].dis-h[xx]);//跳到天上
if(H[x]+now>h[x]||H[x]+now<0)continue;//判断当前能不能爬(不能爬到地下或天上)
if(dist[xx]>dist[x]+edge[i].dis+abss(now)){
dist[xx]=dist[x]+edge[i].dis+abss(now);
H[xx]=H[x]+now-edge[i].dis;// 实时更新H数组
if(!vis[xx]){
vis[xx]=1;
q.push(xx);
}
}
}
}
}
int main(){
freopen("glide.in","r",stdin);
freopen("glide.out","w",stdout);
read(n);read(m);read(x);
for(R int i=1;i<=n;i++)read(h[i]);
for(R int i=1;i<=m;i++){
read(u);read(v);read(w);
add(u,v,w);add(v,u,w);
}
spfa(1);
if(dist[n]==INF)printf("-1\n");
else printf("%lld\n",dist[n]+h[n]-H[n]);//因为题中说要爬到第n棵树的树顶
return 0;
} T3 vestige
描述
作为魔导士的你进入了一片遗迹。遗迹内共有 \(n\) 个密室,编号从 \(1\) 到 \(n\)。密室间由 \(m\) 条双向通道相连通,通道的长度不尽相同。由于遗迹已尘封多年,通道里都充满着污秽。你需要先净化掉所有通道里的污秽,才能迈出探索的脚步。
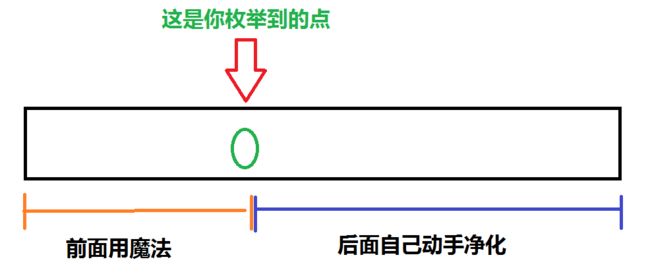
首先,你可以使用神圣驱魔术,净化以 \(1\) 号密室为中心一定区域内所有的道路。当你选定一个非负整数距离 \(X\) 后,消耗 \(C\times X\) 个魔力点(\(C\) 为常数),此时若一条通道两端的密室与 \(1\) 号密室的距离均不大于 \(X\),这条通道就会被净化。之后,你需要分别净化其余通道,净化一条通道所需魔力点数即为这条通道的长度。
请确定净化的方式,使消耗的魔力点数尽可能少。
输入
输入文件第一行包含三个正整数 \(n\), \(m\), \(C\),分别表示密室数量、通道数量和与使用神圣净化术相关的常数。
接下来 \(m\) 行,其中第 \(i\) 行包含 \(3\) 个整数 \(u_i\), \(v_i\), \(d_i\),依次表示第 \(i\) 条通道两端密室的编号和这条通道的长度。
输出
输出一行一个整数,表示消耗魔力点数的最小值。
输入样例 1 :
5 5 2 2 3 1 3 1 2 2 4 3 1 2 4 2 5 5
输出样例 1 :
14
提示
对于 \(32\%\) 的测试数据,\(n\)≤\(100\), \(m\)≤\(200\), \(C\)≤\(100\), \(di\)≤\(10\)。
对于 \(64\%\) 的测试数据,\(n\)≤\(100\), \(m\)≤\(4000\)。
对于 \(100\%\) 的测试数据,满足以下条件:\(2≤n≤100000, 1≤m≤200000, 1≤C≤100000,u_i≠v_i,1≤d_i≤100000\),在两个密室间直接连接的通道不超过一条。
题解
我的歪解
我首先想的是分治,我想二分肯定不行,因为它是没有单调性的。
我想了一下感觉它的大部分数据应该是有凸性的(例如\(y=x^2\)的函数图像),所以可以三分。
下面是我的三分代码(得了84分,可以说骗了不少,当时手贱\(SPFA\)写错了,竟有68分)
三分模板没过的我居然瞎歪歪了一个三分
歪解code:
#include
#include
#include
#include
#include
#include
#define ll long long
#define R register
#define N 400005
#define INF 0x7fffffffffffLL
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
ll n,m,c,tot,h[N],vis[N],pd[N];
ll dist[N],sum,now_ans,now;
struct bian{
int u,v;
ll w;
}b[N];
struct node{
int nex,to;
ll dis;
}edge[N<<1];
inline void add(R int u,R int v,R ll w){
edge[++tot].nex=h[u];
edge[tot].to=v;
edge[tot].dis=w;
h[u]=tot;
}
inline void spfa(R int s){
for(R int i=1;i<=n;i++)dist[i]=INF;
queue q;q.push(s);dist[s]=0;vis[s]=1;
while(!q.empty()){
R int x=q.front();q.pop();vis[x]=0;
for(R int i=h[x];i;i=edge[i].nex){
R int xx=edge[i].to;
if(dist[xx]>dist[x]+edge[i].dis){
dist[xx]=dist[x]+edge[i].dis;
if(!vis[xx]){
vis[xx]=1;
q.push(xx);
}
}
}
}
}
inline ll check(R ll mid){
ll tot=0;
for(R int i=1;i<=n;i++)pd[i]=0;
for(R int i=1;i<=n;i++)
if(dist[i]<=mid)pd[i]=1;
for(R int i=1;i<=m;i++)
if(pd[b[i].u]&&pd[b[i].v])
tot+=b[i].w;
return tot-mid*c;//这是你能节省的
}
int main(){
freopen("vestige.in","r",stdin);
freopen("vestige.out","w",stdout);
read(n);read(m);read(c);
for(R int i=1;i<=m;i++){
read(b[i].u);read(b[i].v);read(b[i].w);
add(b[i].u,b[i].v,b[i].w);add(b[i].v,b[i].u,b[i].w);sum+=b[i].w;
}
spfa(1);
R ll l=0,r=sum;
while(l<=r){
R ll tmp=(r-l)/3;
R ll mid1=l+tmp;
R ll mid2=r-tmp;
if(check(mid1)>check(mid2)) r=mid2-1;
else l=mid1+1;
}
ll tmp=check(l),temp=check(r);
if(tmp>temp)now=l,now_ans=tmp;
else now=r,now_ans=temp;
printf("%lld\n",sum-now_ans);
return 0;
} 当然了,三分本来就是一个非常好的骗分算法(也会是正解),有些题在加一些暴力,一定会有神奇的效果;
讲课老师说加上暴力这道题应该可以\(A\)掉,但懒惰的我并没有去实践,有兴趣的可以试一试;
正解
这其实是一道经典的最短路的一种题型。
先跑一遍\(SPFA\),处理出\(dist\)数组;
然后再利用\(dist\)数组处理出每一条边的\(maxdis\);
将\(maxdis\)数组从小到大排序(结构体排序);
看完图应该都懂了吧。
code:
#include
#include
#include
#include
#include
#include
#define ll long long
#define R register
#define N 800005
#define int long long
#define INF 9999999999999999LL
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
ll n,m,c,tot,h[N],vis[N],pd[N],maxdis[N];
ll dist[N],sum,ans,maxsum;
struct bian{
int u,v,w;
}b[N];
struct node{
int nex,to,dis;
}edge[N<<1];
struct MAX{
int maxdis,id;
friend bool operator < (const MAX &a,const MAX &b){
return a.maxdis q;q.push(s);dist[s]=0;vis[s]=1;
while(!q.empty()){
R int x=q.front();q.pop();vis[x]=0;
for(R int i=h[x];i;i=edge[i].nex){
R int xx=edge[i].to;
if(dist[xx]>dist[x]+edge[i].dis){
dist[xx]=dist[x]+edge[i].dis;
if(!vis[xx]){
vis[xx]=1;
q.push(xx);
}
}
}
}
}
signed main(){
freopen("vestige.in","r",stdin);
freopen("vestige.out","w",stdout);
read(n);read(m);read(c);
for(R int i=1;i<=m;i++){
read(b[i].u);read(b[i].v);read(b[i].w);
add(b[i].u,b[i].v,b[i].w);add(b[i].v,b[i].u,b[i].w);sum+=b[i].w;
}
spfa(1);
for(R int i=1;i<=m;i++)
md[i].maxdis=max(dist[b[i].u],dist[b[i].v]),md[i].id=i;
sort(md+1,md+1+m);
ans=sum;
for(R int i=1;i<=m;i++){
sum-=b[md[i].id].w;
ans=min(ans,1LL*md[i].maxdis*c+sum);
}
printf("%lld\n",ans);
return 0;
} T4 copy
描述
从前有一个$ {1, 2, \dots , n}$ 的排列,你希望用剪切/粘贴操作,将这个排列变成 \(1,2, \dots , n\)。
一次剪切/粘贴操作指的是把序列中某段连续的子区间整体向前或者向后平移一段距离。由于你认为同时按 $Ctrl+X $很累手指,所以想要知道最少的操作次数。
输入
输入文件包含多组数据。
每组数据有两行,其中第一行包含一个正整数 \(n\),第二行给出一组 \({1, 2, ..., n}\) 的排列。
以一个 \(0\) 来结束输入。
输出
对于每组数据,输出一行一个整数,表示最小的操作次数。
输入样例 1:
6 2 4 1 5 3 6 5 3 4 5 1 2 0
输出样例 1 :
2 1
提示
对于 \(20 \%\) 的数据,数据组数 \(\leq 6\)。
对于\(100\%\) 数据,\(n \leq 9\),数据组数 \(\leq 50\)。
题解
\(IDA^*\)的一道很不错的题
但是还是讲一下粗略的讲\(IDA^*\),(我觉得可能一些人并不了解);
一道入门题
以\([SCOI2005]\)骑士精神为例,先讲一下\(IDA^*\)的基础前置知识;
突然加上一道题。。。
T4+ [SCOI2005]骑士精神
描述
在一个\(5×5\)的棋盘上有\(12\)个白色的骑士和\(12\)个黑色的骑士, 且有一个空位。在任何时候一个骑士都能按照骑
士的走法(它可以走到和它横坐标相差为\(1\),纵坐标相差为\(2\)或者横坐标相差为\(2\),纵坐标相差为\(1\)的格子)移动到空
位上。 给定一个初始的棋盘,怎样才能经过移动变成如下目标棋盘: 为了体现出骑士精神,他们必须以最少的步
数完成任务。
输入
第一行有一个正整数\(T(T<=10)\),表示一共有\(N\)组数据。接下来有\(T\)个\(5×5\)的矩阵,\(0\)表示白色骑士,\(1\)表示黑色骑 士,\(*\)表示空位。两组数据之间没有空行。
输出
对于每组数据都输出一行。如果能在\(15\)步以内(包括\(15\)步)到达目标状态,则输出步数,否则输出-\(1\)。
输入样例 1:
2 10110 01*11 10111 01001 00000 01011 110*1 01110 01010 00100
输出样例1:
7 -1
题解
题意:给你一个初始棋盘,要求用最少的步数移动马达到如上图的目标状态(要求棋盘中的马只能走“日”)。
咱们先抛开\(IDA^*\),先如何优化爆搜;
这里的马和象棋里的马走法相同,但题目中要求让马走,但是要是马的话,搜索分支比较多,所以我们要考虑让空格走(很显然吧)。
下面步入正题:
\(IDA^*\)就是带有迭代加深和估价函数优化的搜索。
可能某些人对以上两个名词很陌生,下面一些前置知识可能会带你透彻一下。
前置知识1:迭代加深
定义:
每次限定一个\(maxdep\)最大深度,使搜索树的深度不超过\(maxdep\)。
for(R int maxdep=1;maxdep<=题目中给的最大步数;maxdep++){
dfs(0,maxdep);//0为出入函数中当前步数,maxdep为传入的最大深度。
if(success)break;//如果搜索成功则会在dfs函数中将success赋值为1。
}使用范围:
1.在有一定的限制条件时使用(例如本题中“如果能在\(15\)步以内(包括\(15\)步)到达目标状态,则输出步数,否则输出\(-1\)。“)。
2.题目中说输出所以解中的任何一组解。
为什么能够降低时间复杂度:
我们可能会在一个没有解(或解很深的地方无限递归然而题目中要求输出任何的一组解),所以我们限制一个深度,让它去遍历更多的分支,去更广泛地求解,(其实和\(BFS\)有异曲同工之妙)。
前置知识2:估价函数
定义:
\(f(n)=g(n)+h(n)\)
其中\(f(n)\)是节点的估价函数,\(g(n)\)是现在的实际步数,\(h(n)\)是对未来步数的最完美估价(“完美”的意思是可能你现实不可能实现,但你还要拿最优的步数去把\(h(n)\)算出来,可能不太好口胡,可以参考下面的实例)。
应用:
void dfs(int dep,int maxdep){
if(evaluate()+dep>maxdep)return;
//evaluate函数为对未来估价的函数,若未来估价加实际步数>迭代加深的深度则return。
if(!evaluate){
success=1;
printf("%d\n",dep);
return;
}
......
}前置知识3:\(A^*\)和\(IDA^*\)的区别
\(A^*\)是用于对\(BFS\)的优化;
\(IDA^*\)是对结合迭代加深的\(DFS\) 的优化。
本质上只是在\(BFS\)和\(DFS\)上加上了一个估价函数。
何时使用因题而定:
\(A^*\)([SCOI2007]k短路);\(IDA^*\)([SCOI2005]骑士精神和UVA11212 Editing a Book 就是上面的两道题)。
前置知识毕!!!
现在就是要想一个比较好的估价函数(若估价函数不好的话,优化效率就并不高,例如若估价函数一直为0,那就是爆搜)。
我们可以想一下,每次空白格子和黑白棋子交换,最优的情况就是每次都把黑白棋子移动到目标格子。
那么你的估价函数就出来了:
const int goal[7][7]={
{0,0,0,0,0,0},
{0,1,1,1,1,1},
{0,0,1,1,1,1},
{0,0,0,2,1,1},
{0,0,0,0,0,1},
{0,0,0,0,0,0}
};
inline int evaluate(){
R int cnt=0;
for(R int i=1;i<=5;i++)
for(R int j=1;j<=5;j++)
if(mp[i][j]!=goal[i][j])cnt++;
return cnt;
}下面就是爆搜了:
#include
#include
#include
#include
#include
#define ll long long
#define R register
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
int n,m,t,mp[7][7],stx,sty,success;
char ch;
const int dx[]={0,1,1,-1,-1,2,2,-2,-2};
const int dy[]={0,2,-2,2,-2,1,-1,1,-1};
const int goal[7][7]={
{0,0,0,0,0,0},
{0,1,1,1,1,1},
{0,0,1,1,1,1},
{0,0,0,2,1,1},
{0,0,0,0,0,1},
{0,0,0,0,0,0}
};
inline int evaluate(){
R int cnt=0;
for(R int i=1;i<=5;i++)
for(R int j=1;j<=5;j++)
if(mp[i][j]!=goal[i][j])cnt++;
return cnt;
}
inline int safe(R int x,R int y){
if(x<1||x>5||y<1||y>5)return 0;
return 1;
}
inline void A_star(R int dep,R int x,R int y,R int maxdep){
if(dep==maxdep){
if(!evaluate())success=1;
return;
}
for(R int i=1;i<=8;i++){
R int xx=x+dx[i];
R int yy=y+dy[i];
if(!safe(xx,yy))continue;
swap(mp[x][y],mp[xx][yy]);
int eva=evaluate();
if(eva+dep<=maxdep)
A_star(dep+1,xx,yy,maxdep);
swap(mp[x][y],mp[xx][yy]);//回溯
}
}
int main(){
read(t);
while(t--){
success=0;
for(R int i=1;i<=5;i++){
for(R int j=1;j<=5;j++){
cin>>ch;
if(ch=='*')mp[i][j]=2,stx=i,sty=j;//记录起点即为空白格子
else mp[i][j]=ch-'0';
}
}
if(!evaluate()){printf("0\n");continue;}
for(R int maxdep=1;maxdep<=15;maxdep++){
A_star(0,stx,sty,maxdep);
if(success){printf("%d\n",maxdep);goto ZAGER;}
}
printf("-1\n");
ZAGER:;
}
return 0;
} \(IDA^*\)入门铺垫完成。。。终于到T4了
大致题意:给出一个1~n的排列,每次可以交换相邻两个区间,问最少移动几次使其变成1,2,3...n。
本题若是想用\(IDA^*\)便是考察估价函数的设计(本题估价函数确实不好设计)。
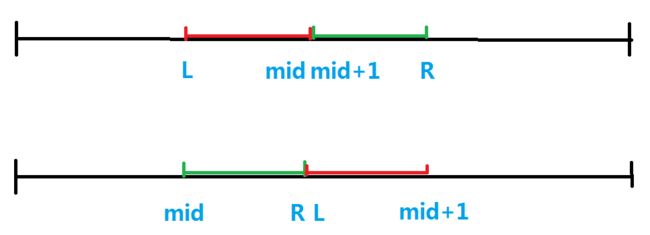
若这个区间是连续的那么
画一个图想一下
code(没有任何其他剪枝,不动任何的思维):
#include
#include
#include
#include
#include
#include
#define ll long long
#define R register
#define N 10
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
int n,maxdep,num[N],tmp[N],success;
inline int gujia(){
R int tot=0;
for(R int i=1;i<=n-1;i++)
if(num[i+1]!=num[i]+1) tot++;
tot+=(num[n]!=n);
return (tot+2)/3;
}
inline void ctrl_x(R int l,R int mid,R int r){
R int now=l;
for(R int i=mid+1;i<=r;i++)
tmp[now++]=num[i];
for(R int i=l;i<=mid;i++)
tmp[now++]=num[i];
for(R int i=l;i<=r;i++)
num[i]=tmp[i];
}
inline void dfs(R int dep){
if(success)return;
R int zager=gujia();
if(zager+dep>maxdep)return;
if(!zager){
printf("%d\n",dep);
success=1;return;
}
for(R int l=1;l<=n-1;l++){
for(R int mid=l;mid<=n-1;mid++){
for(R int r=mid+1;r<=n;r++){
ctrl_x(l,mid,r);
dfs(dep+1);
if(success)return;
ctrl_x(l,l+r-mid-1,r);
}
}
}
}
inline void IDAstar(){
success=0;
for(maxdep=1;maxdep;maxdep++){
dfs(0);
if(success)break;
}
}
int main(){
freopen("copy.in","r",stdin);
freopen("copy.out","w",stdout);
while(233){
read(n);
if(!n)break;
for(R int i=1;i<=n;i++)read(num[i]);
IDAstar();
}
return 0;
} T5 trainfair
描述
在 \(MS\) 国有 \(N\) 座城市,编号从 \(1\) 到 \(N\) ,其中 \(1\) 号城市是 \(MS\) 国的首都。
\(MS\) 国里,只有一家铁路公司,经营着 \(M\) 条连接着各城市的铁路线路,每条线路都双向地连接着两座不同的城市。通过这些线路,我们可以在任意两座城市间通行。
原本,乘坐一条线路只需要花费 \(1\) 角钱。可是由于经营不善,铁路公司提出计划,要在今后的 \(Q\) 年间,每年给某一条线路涨价为 \(2\) 角钱。保证一条线路不会被涨价多次。
另外,这个铁路公司每年都会在每一座城市进行一次居民满意度调查。原本每一座城市中的居民都对铁路公司的服务十分满意,但在线路涨价后就说不定了。每一年的满意度调查都会在当年的涨价计划实施后进行。如果一座城市中的居民在当年坐火车去首都所需的最少花费相比于计划提出前增加了,他们就会对铁路公司抱有不满。首都的居民永远不会对铁路公司抱有不满。
在计划施行前,你需要帮助铁路公司统计出未来的每一年中,各将有多少城市的居民对铁路公司抱有不满。
输入
输入文件第一行包含三个正整数 \(N\), \(M\), \(Q\),分别表示 \(MS\) 国的城市数量、铁路路线数量和涨价计划将要实施的时间长度。
接下来 \(M\) 行,其中第 \(i\) 行包含 \(2\) 个整数 \(U_i, V_i\),表示第 \(i\) 条路线连接着编号为 \(U_i\) 和 \(V_i\) 的两座城市。
接下来 \(Q\) 行,其中第 \(j\) 行包含一个整数 \(R_j\),表示计划施行后第 \(j\) 年将会让第 \(R_j\) 条线路涨价。
输出
输出 \(Q\) 行,其中第 \(j\) 行表示第 \(j\) 年居民对铁路公司抱有不满的城市的数量。
输入样例 1 :
5 6 5 1 2 1 3 4 2 3 2 2 5 5 3 5 2 4 1 3
输出样例 1
0 2 2 4 4
提示
对于 \(24\%\) 的测试数据,\(N \leq 100, M \leq 4950, Q \leq 30\)。
对于 \(48\%\) 的测试数据,\(Q \leq 30\)。
对于另 \(32\%\) 的测试数据,正确的输出中不同的数字不超过\(50\) 种。
对于 \(100\%\) 的测试数据,满足以下条件:
\(2 \leq N \leq 10^5, 1 \leq Q \leq M \leq 2 \times 10^5\),
\(1 \leq U_i, V_i \leq N, U_i ≠ V_i,1 \leq R_j \leq M\),且两个城市间直接连接的路线不超过一条。
题解
大致题意:\(N\)个点\(M\)条边,初始边权均为1,每次修改一条边的权值,问每次修改后有几个点的到1的最短路与初始最短路的长度不同。
我的暴力思路(60分)
首先\(48\%\)数据的可以发现\(Q\)很小,使用暴力修改(其实是\(O(1)\))暴力\(Q\)遍\(SPFA\),每次暴力统计\(ans\)。
为什么能过\(60\%\)的数据呢(好像是数据水)。
我们可以想一下,假如我们修改过一条边,那么下次再次修改的时候就已经没有贡献了,所以可以用\(used\)数组标记,如果标记过直接输出上次的\(ans\)。
#include
#include
#include
#include
#include
#include
#include
#define ll long long
#define R register
#define INF 0x3f3f3f3f
#define N 200005
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
int n,m,q,u,v,tot,x,ans;
int h[N],used[N],id[N],dist[N],vis[N],last[N];
struct node{
int nex,to,dis;
}edge[N<<1];
inline void add(R int u,R int v,R int w){
edge[++tot].nex=h[u];
edge[tot].to=v;
edge[tot].dis=w;
h[u]=tot;
}
inline void spfa(R int s){
queue q;
for(R int i=1;i<=n;i++)dist[i]=INF,vis[i]=0;
q.push(s);vis[s]=1;dist[s]=0;
while(!q.empty()){
R int x=q.front();q.pop();vis[x]=0;
for(R int i=h[x];i;i=edge[i].nex){
R int xx=edge[i].to;
if(dist[xx]>dist[x]+edge[i].dis){
dist[xx]=dist[x]+edge[i].dis;
if(!vis[xx]){
vis[xx]=1;q.push(xx);
}
}
}
}
}
int main(){
freopen("trainfair.in","r",stdin);
freopen("trainfair.out","w",stdout);
read(n);read(m);read(q);
for(R int i=1;i<=m;i++){
read(u);read(v);
add(u,v,1);add(v,u,1);
id[i]=tot;//记录边的序号
}
spfa(1);
for(R int i=1;i<=n;i++)last[i]=dist[i];//初始最短路的值
for(R int i=1;i<=q;i++){
read(x);
edge[id[x]].dis+=2;
edge[id[x]-1].dis+=2;//修改
if(used[x])printf("%d\n",ans);//标记
else{
spfa(1);ans=0;//暴力SPFA
for(R int j=1;j<=n;j++)
if(dist[j]!=last[j])ans++;//暴力统计ans
printf("%d\n",ans);
used[x]=1;
}
}
fclose(stdin);
fclose(stdout);
return 0;
} 正解
正解和上面的暴力思路可以说是没有多少相似的地方。。。
大致思路:
在原图上跑一边\(SPFA\)(或\(Dij\)堆优化),目的是处理出最短路数组\(dist\)。
重新建一个关于最短路的拓扑图,即如果满足最短路\(dist[xx]==dist[x]+edge[i].dis\)的性质则建边,由于我们在原图从\(1\)开始跑,而我们要的拓扑图是要从每个点连到\(1\),所以要反向建边,并且统计每个点的出度。
inline void bfs(R int x){ for(R int x=1;x<=n;++x){ for(R int i=h[x];i;i=edge[i].nex){ R int xx=edge[i].to; if(dist[xx]==dist[x]+edge[i].dis) ADD(xx,x,edge[i].dis,edge[i].id);chu[xx]++;nxt[i/2]=xx; } } }下面就是核心的
#include
#include
#include
#include
#include
#include
#include
#define ll long long
#define R register
#define INF 0x3f3f3f3f
#define N 200005
using namespace std;
templateinline void read(T &a){
char c=getchar();T x=0,f=1;
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
a=f*x;
}
int n,m,q,u,v,tot=1,opt,ans,t=1;
int h[N],used[N],dist[N],vis[N],head[N],chu[N],nxt[N];
struct node{
int nex,to,dis,id;
}edge[N<<1],e[N<<1];
inline void ADD(R int u,R int v,R int w,R int id){
e[++t].nex=head[u];
e[t].to=v;
e[t].dis=w;
e[t].id=id;
head[u]=t;
}
inline void add(R int u,R int v,R int w,R int id){
edge[++tot].nex=h[u];
edge[tot].to=v;
edge[tot].dis=w;
edge[tot].id=id;
h[u]=tot;
}
inline void spfa(R int s){
queue q;
for(R int i=1;i<=n;i++)dist[i]=INF;
q.push(s);vis[s]=1;dist[s]=0;
while(!q.empty()){
R int x=q.front();q.pop();vis[x]=0;
for(R int i=h[x];i;i=edge[i].nex){
R int xx=edge[i].to;
if(dist[xx]>dist[x]+edge[i].dis){
dist[xx]=dist[x]+edge[i].dis;
if(!vis[xx]){
vis[xx]=1;q.push(xx);
}
}
}
}
}
inline void bfs(R int x){
for(R int x=1;x<=n;++x){
for(R int i=h[x];i;i=edge[i].nex){
R int xx=edge[i].to;
if(dist[xx]==dist[x]+edge[i].dis){
ADD(xx,x,edge[i].dis,edge[i].id);chu[xx]++;nxt[i/2]=xx;
}
}
}
}
queue Q;
int main(){
freopen("trainfair.in","r",stdin);
freopen("trainfair.out","w",stdout);
read(n);read(m);read(q);
for(R int i=1;i<=m;i++){
read(u);read(v);
add(u,v,1,i);add(v,u,1,i);
}
spfa(1);
bfs(1);tot=1;
memset(h,0,sizeof(h));
for(R int i=1;i<=n;i++){
for(R int j=head[i];j;j=e[j].nex){
R int xx=e[j].to;
add(xx,i,e[j].dis,e[j].id);
}
}
while(q--){
read(opt);R int x=nxt[opt];
if(used[opt]||x==0){printf("%d\n",ans);continue;}
used[opt]=1;chu[x]--;
if(!chu[x]){
Q.push(x);
while(!Q.empty()){
R int u=Q.front();Q.pop();ans++;
for(R int i=h[u];i;i=edge[i].nex){
R int v=edge[i].to;
if(used[edge[i].id])continue;
used[edge[i].id]=1;
chu[v]--;if(!chu[v])Q.push(v);
}
}
}
printf("%d\n",ans);
}
fclose(stdin);
fclose(stdout);
return 0;
}