Squeeze-and-Excitation Networks(2019)
Abstract
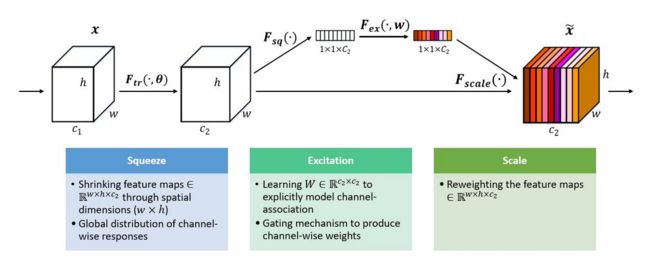
传统的卷积操作使得网络可以聚合空间和通道信息并建立informative features。大量研究致力于通过提高空间编码(spatial encodings)的质量来增强网络的表达能力(representational power)。 本论文中, 作者的关注点是channel relationship并提出了一个新的框架单元,将其命名为SE block,它能够自适应地基于通道间关联反复调整通道特征。这一框架具有较强的泛化能力。
Introduction
SE building block 结构图:
Related Work:
Deeper architectures
加深网络深度(VGGNets, Inception);使用更具有表达力的运算(group convolution)
Algorithmic Architecture Search
通过算法使得网络结构自动进化
Attention and gating mechanisms
Attention can be interpreted as a means of biasing the allocation of available computational resources towards the most informative components
此前提出的trunk-and-mask 注意力机制可用于空间和通道注意力,但本文提出的SeNet更加轻量级
Squeeze-and-excitation Blocks
Squeeze: Global Information Embedding
由于每个输出单元只能反映其接受野的信息而无法获得此区域之外的背景信息,为减少这一问题,我们提出,将全局空间信息压缩成一个通道描述子
\[ z_c=F_{sq}(u_c)=\frac {1}{H\times W} \sum_{i=1}^{H} \sum _{j=1}^{W} u_c(i,j) \]
Excitation: Adaptive Recalibration
为了全面的捕捉通道间依赖关系,excite函数必须满足以下2点:
- flexible (in particular, it must be capable of learning a nonlinear interaction between channels)
- learn a non-mutually-exclusive relationship (we would like to ensure that multiple channels are allowed to be emphasised rather than enforcing a one-hot activation)
因此,我们采用一个简单的门机制,使用sigmoid函数激活:
\[ s=F_{ex}(z,W) = \sigma (g(z,W)) = \sigma (W_2 \delta (W_1z)) \]
其中,$\delta $ 是ReLU 函数,$ W_1 \in R^{\frac{C}{r} \times C} $, $ W_2 \in R^{C \times \frac{C}{r}} $.
为了限制模型复杂度,增强泛化能力,我们参数化门机制,在非线性处使用2层全连接层来形成一个瓶颈,即一个以reduction ratio r为参数的降维层。该模块的最终输出为:
\[ \widetilde x_c=F_{scale}(u_c,s_c)=s_cu_c \]
\[ \widetilde X=[\widetilde x_1,\widetilde x_2,...\widetilde x_c] \]
Instantiations
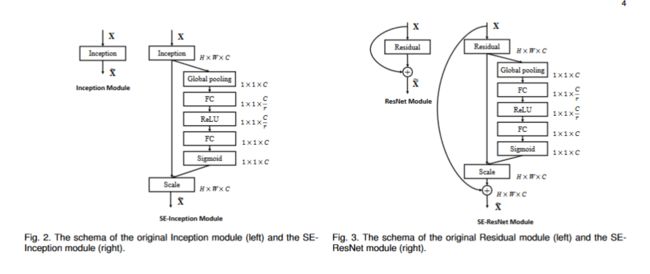
SE block 能够被整合进标准框架(插入在卷积层之后的非线性层后),甚至可以被用于标准卷积后的变换。
Model and Computational Complexity
额外引入的参量数为 $ \frac {2}{r} \sum_{i=1}^{s}N_s\cdot C_s^2 $,其中s为block数量,增加的计算复杂度~10%,相比于增加网络深度效率很高。
名词解释
receptive field
卷积神经网络每一层输出的特征图(feature map)上的像素点在原始图像上映射的区域大小
ablation experiment
剥离试验