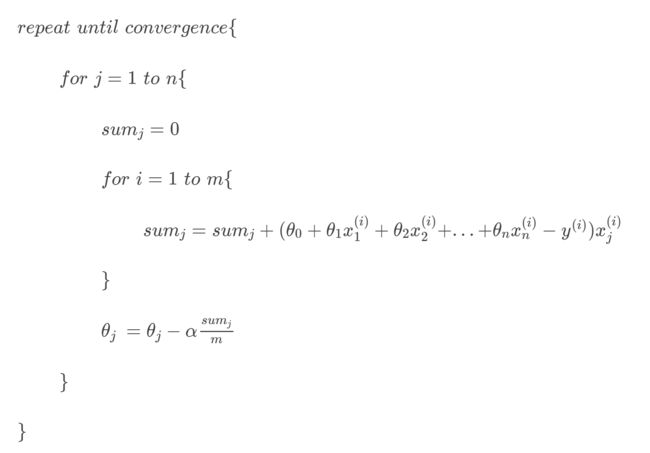第10课:线性回归– 从模型函数到目标函数
1. 机器学习的目标是使我们建立的模型运行结果和理想结果之间的差异尽可能小,因此可以将目标函数建模成为一个对这类差异的评估函数,求解使得目标函数最小值的一个最优化的问题。
2. 第一步,从数据反推公式。在已知数据情况下,试建立模型并不断调试,直至确认模型参数最优以达到理想结果和模型训练结果之间差异最小化的结果。举例如下:
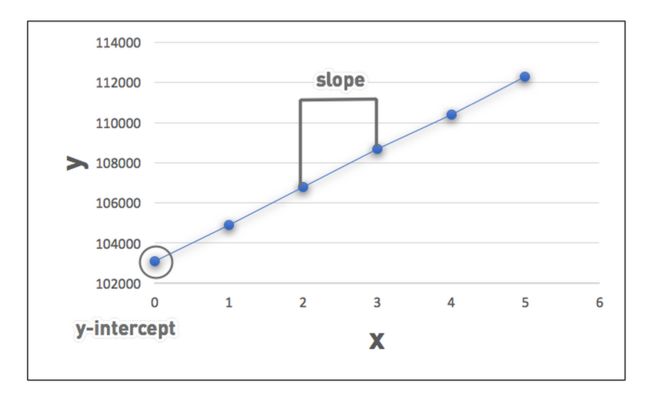
3. 第二步,通过提取Experience和Salary并用x和y分别指代他们,发现y和x之间的正比关系。从而得出y=a+bx这样的线性相关关系。
4. 综合利用训练数据,拟合线性回归函数,就是我们要求的模型函数。模型函数和目标函数的差异最小,就是我们不断训练模型要得到的目标。
假如我们要求的模型函数是这样的一个一元线性函数,那么衡量模型函数和目标函数之间的差距就可以表达为:
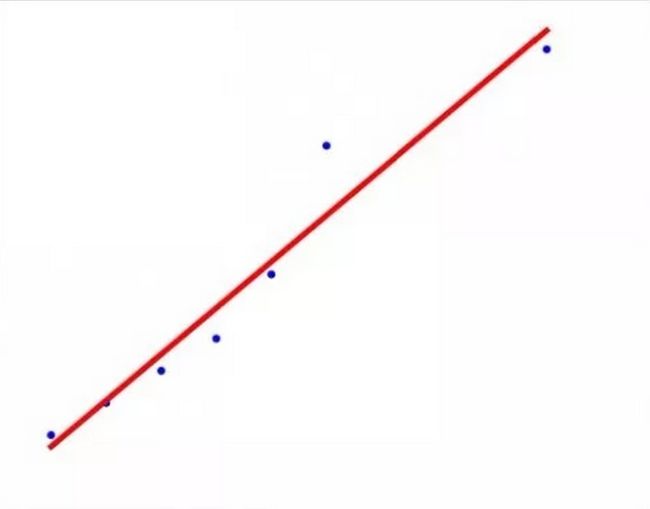
数据拟合成为直线的效果如下图所示
5 利用线性函数对一个或多个自变量和因变量之间的关系进行拟合的模型。线性函数的定义是:一阶多项式,或零多项式。当线性函数只有一个自变量时,y=f(x).
f(x) 的函数形式是:f(x) = a + bx (a、b 为常数,且 b≠0b≠0)——一阶多项式
或者 f(x) = c (c 为常数,且 c≠0c≠0) —— 零阶多项式
或者 f(x) = 0 —— 零多项式
总结一下:特征是一维的,线性模型在二维空间构成一条直线;特征是二维的,线性模型在三维空间中构成一个平面;若特征是三维的,则最终模型在四维空间中构成一个体,以此类推。
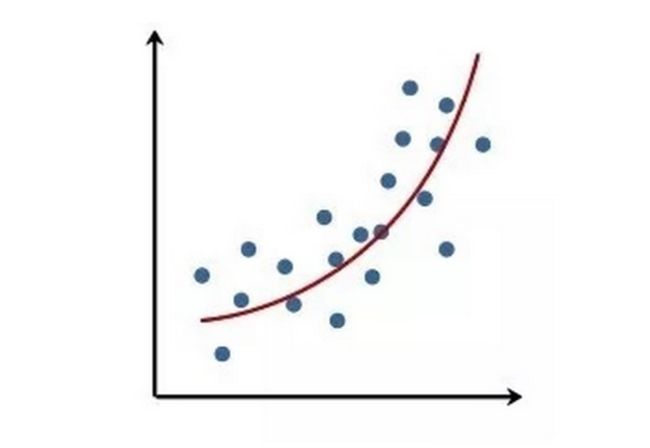
用线性回归模型拟合非线性关系
拟合的结果就是X=(x1, x2)(其中x1=x2;x2=x),有:
第11课:线性回归– 梯度下降法求解目标
如下所示,J(a,b)是一个二元函数,我们的目标是求取理想的参数a和b的值,并且当a,b达到这个值的时候,J(a,b)的值达到最小。
斜率、导数和偏微分
当求取以曲线表示的函数在某一点的导数值的时候,就是求取经过这个点的函数曲线切线的斜率。
一元函数在某一点处沿 x 轴正方向的变化率称为导数。但如果是二元或更多元的函数(自变量维度 >=2),则某一点处沿某一维度坐标轴正方向的变化率称为偏导数。
导数/偏导数表现的是变化率,而变化本身,用另一个概念来表示,这个概念就是微分(对应偏导数,二元及以上函数有偏微分)。
(偏)导数是针对函数上的一个点而言的,是一个值。而(偏)微分则是一个函数,其中的每个点表达的是原函数上各点沿着(偏)导数方向的变化。
直观而不严格的来说,(偏)微分就是沿着(偏)导数的方向,产生了一个无穷小的增量。
当我们求出了一个函数的(偏)微分函数后,将某个变量带入其中,得出的(偏)微分函数对应的函数值,就是原函数在该点处,对该自变量求导的导数值。
梯度下降中的步长参数阿尔法α是无法求解的,必须手工指定。
如果训练程序是通过人工制定迭代次数来确定退出条件,则迭代次数也是一个超参数。
如果训练程序以模型结果与真实结果的整体差值小于某一个阈值为退出条件,则这个阈值就是超参数。
在模型类型和训练数据确定的情况下,超参数的设置就成了影响模型最终质量的关键。
而往往一个模型会涉及多个超参数,如何制定策略在最少尝试的情况下让所有超参数设置的结果达到最佳,是一个在实践中非常重要又没有统一方法可以解决的问题。
importmatplotlib.pyplot as plt
importnumpy as np
fromsklearn import datasets, linear_model
fromsklearn.metrics import mean_squared_error, r2_score
experiences = np.array([0,1,2,3,4,5,6,7,8,9,10])
salaries= np.array([103100, 104900, 106800, 108700, 110400, 112300, 114200, 116100,117800, 119700, 121600])
#将特征数据集分为训练集和测试集,除了最后 4 个作为测试用例,其他都用于训练
X_train =experiences[:7]
X_train =X_train.reshape(-1,1)
X_test =experiences[7:]
X_test =X_test.reshape(-1,1)
#把目标数据(特征对应的真实值)也分为训练集和测试集
y_train =salaries[:7]
y_test =salaries[7:]
#创建线性回归模型
regr =linear_model.LinearRegression()
#用训练集训练模型——看就这么简单,一行搞定训练过程
regr.fit(X_train, y_train)
#用训练得出的模型进行预测
diabetes_y_pred = regr.predict(X_test)
#将测试结果以图标的方式显示出来
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()