Edward系列（二）

继续讲线性混合效应模型。

苏黎世联邦理工学院评选“谁是最可爱的教授”。2972名学生评价1128名教授/教师的讲座，学生来自在14个院系的不同年级。每名教师可能会开设多个讲座，每名学生可能会评价多个讲座。数据集如下。

数据集来自R包lme4，总共有73421条数据

很多人认为模型就是由输入产生输出的过程。按这种想法，上面这个数据集，输入是s、d、studage、lectage、service、dept，输出就是y，我们希望模型对y的预测是准确的。

但模型也可以反过来“由果溯因”。这时候，我们希望通过y这个结果，反推一些事实。例如Edward文档中提到：

摘自：http://edwardlib.org/tutorials/linear-mixed-effects-models

意思是：有些学生会“不用脑”的给所有讲座打高分（或低分）;好老师的讲座应该更受欢迎;有些院系只出“干货”，不会包装，所以分数低。

复杂一点说就是：独立性假设不成立。

问题来了，我们能不能把“不用脑”的同学识别出来？能不能把高出一般水平的好老师识别出来？能不能把那些“内向有才华”的院系识别出来？

办法是有的。

我们先看一下独立性假设成立时模型是什么样子的。这个前提下，所有同学都是“有脑”的，所有老师都是好老师，所有院系都是“英俊有才华”的。

摘自：http://edwardlib.org/tutorials/linear-mixed-effects-models，注释是我加的

从这张图可以看到，在独立性假设下，我们用典型的线性回归模型就可以了。可是，我们用了73421条数据，最终获得的居然只有5个系数，这也太“浪费”数据了。

不“浪费”数据的办法也是有的。例如，我们用特征工程的办法，把某些变量稀疏表示（参见周志华《机器学习》11.5）。我举个风控的例子。

稀疏表示后，MaxDqBin变成了6个新变量MaxDqBin01～MaxDqBin06

把原始变量稀疏表示后，再建模得到的系数就相应变多了。下面是建模后得到的信息。

多了10个新系数，开不开心？

原本我们通过建模只能获得5个系数（分别对应Intercept、TOB、NonBankTradeDq、IncomeLevel、MaxDqBin），但通过变量稀疏表示（NonBankTradeDq变成NonBankTradeDq01～06，MaxDqBin变成MaxDqBin01～06），新模型获得了15个系数。观察NonBankTradeDq01～06的系数，02、04、06的系数是负值，01、03、05系数是正值，说明即使同一个变量，其内部差异对最终结果的影响是不同的，所以，把变量“拆开”（稀疏表示）是必要的。

这引申出一个新的问题。什么样的稀疏表示才是合适的？为什么MaxDqBin“拆成”6个变量，而不是20个？

很多人的回答是：找领域专家。有时候专家有很大作用，有时候这么做只是把问题交给“色子”。

掷色子，果个人都会啊！

或者能不能更进一步，一个变量有多少唯一值就“拆成”多少个新变量？回到“谁是最可爱的教授”这个例子，学生变量s，有2972名学生，“拆成”2972个新变量，老师变量d，有1128名老师，“拆成”1128个新变量，以此类推。可是，新增加多少个新变量，就意味着新增加多少个要估计的系数，这是一个可以完成的任务吗？

这也是线性混合效应模型要解决的问题。引用一本线性模型引论的话：近30年来，关于混合效应模型的参数估计一直是线性模型的最活跃的研究方向之一。

Edward回答了这个问题：Yes，I can do！

当然在 Edward 之前还有很多工具解决了这个问题。例如，R包lme4。lme4 用的方法和 Edward的方法是不一样的，Edward用的是贝叶斯方法+Tensorflow（或者深度概率编程），lme4的作者在lme4文档里，这样说：混合效应模型虽然很有用，但超大的计算量把它限制在中等数据集（一万到一百万）的建模上。Edward建在Tensorflow之上，估计是可以突破中等数据集这层限制的。

lme4无法突破中等数据集限制

我们还是把线性混合效应模型的数学表达形式展示出来。

确定只是增加了一点点？

如果数据集不大的话，我还是倾向使用lme4的。因为用lme4建模，只需要一句话。

高度抽象化的编程语言是极好的！

用Edward实现建模，编程就稍微麻烦一些，代码量大概是这些。

如果不和lme4比，其实也不多吧

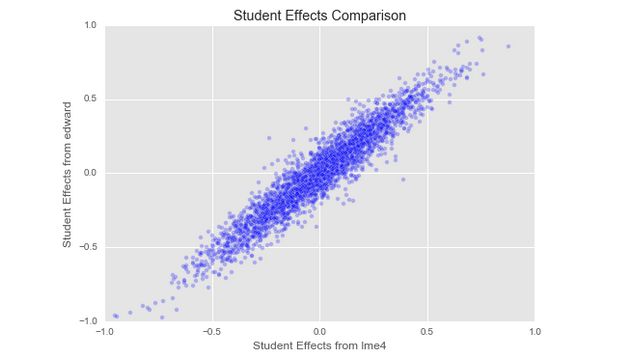
最后，在“谁是最可爱的教授”这个案例，Edward给出了与lme4之间的比较。下图是关于学生的参数（系数）估计。

摘自Edward。横坐标是lme4的计算结果，纵坐标是Edward的计算结果。图上每个点代表了一名学生，有了这些参数估计，我们就可以进一步将学生分类，例如：轻度“不用脑”、中度“不用脑”、。。。这样我们就从数据出发，得出我们希望的结果，而不用受制于某些不靠谱“专家”了。

关于线性混合效应模型的解释，教科书或Edward没有提到稀疏表示，我只是想从稀疏表示这个角度去看待混合效应模型，从工作经验去想一个事情和从理论去想一个事情还是不一样的。

当然，还是要以教科书为主。