一:排序算法
排序方式有插入排序,选择排序和交换排序三种。插入排序有直接插入排序和希尔排序。选择排序有简单选择排序和堆排序。交换排序有冒泡排序和快速排序。
1.冒泡排序算法
基本思想:
冒泡算法是一种基础的排序算法,这种算法会从后向前或从前向后两两比较相邻元素的值,若为逆序,则交换之,直到序列比较完。这一比较会重复n-1趟,每一趟比较n-1-i次,i是已经排序好的元素个数。每一趟比较都能找出未排序元素中最大或者最小的那个数字。这就如同水泡从水底逐个飘到水面一样。冒泡排序是一种时间复杂度较高,效率较低的排序方法。其空间复杂度是O(n)。
(1), 最差时间复杂度 O(n^2)
(2), 平均时间复杂度 O(n^2)
实现思路:
(1),每一趟比较都比较数组中两个相邻元素的大小
(2),如果i元素小于i-1元素,就调换两个元素的位置
(3),重复n-1趟的比较
2.快速排序
基本思想:
实现思路:
(1). 从数列中挑出一个元素,称为 "基准"(pivot),
(2). 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割之后,该基准是它的最后位置。这个称为分割(partition)操作。
(3). 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
快速排序是基于分治模式处理的,对一个典型子数组A[p...r]排序的分治过程为三个步骤:
(1).分解:
A[p..r]被划分为俩个(可能空)的子数组A[p ..q-1]和A[q+1 ..r],使得
A[p ..q-1] <= A[q] <= A[q+1 ..r]
(2).解决:通过递归调用快速排序,对子数组A[p ..q-1]和A[q+1 ..r]排序。
(3).合并。
递回的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递回下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
复杂度:
平均时间复杂度:O(n^2)
平均空间复杂度:O(nlogn) O(nlogn)~O(n^2)
3.直接插入排序
实现思路:将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
4.希尔排序
实现思路:希尔排序是1959 年由D.L.Shell 提出来的,相对直接排序有较大的改进。希尔排序又叫缩小增量排序。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
5.简单选择排序
思路:在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数当中再找最小(或者最大)的与第2个位置的数交换,依次类推,直到第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。
6.堆排序
思路:堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆的定义如下:具有n个元素的序列(k1,k2,...,kn),当且仅当满足
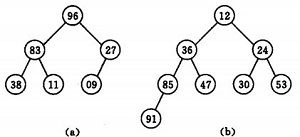
时称之为堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最小项(小顶堆)。若以一维数组存储一个堆,则堆对应一棵完全二叉树,且所有非叶结点的值均不大于(或不小于)其子女的值,根结点(堆顶元素)的值是最小(或最大)的。如:
(a)大顶堆序列:(96, 83,27,38,11,09)
(b) 小顶堆序列:(12,36,24,85,47,30,53,91)
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树(一维数组存储二叉树),调整它们的存储序,使之成为一个堆,将堆顶元素输出,得到n 个元素中最小(或最大)的元素,这时堆的根节点的数最小(或者最大)。然后对前面(n-1)个元素重新调整使之成为堆,输出堆顶元素,得到n 个元素中次小(或次大)的元素。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。称这个过程为堆排序。
参考:喜啦啦的《iOS 排序算法(冒泡、选择、快速、插入、希尔、归并、基数、堆排序)》,陌路行者的《iOS排序算法》。