2018-01-31 转载知乎：如何直观理解矩阵和线性代数？

转载知乎：如何直观理解矩阵和线性代数？

链接：https://www.zhihu.com/question/21082351/answer/126177114

这个系列视频讲得比较全了，都是动画演示，非常直观。自己按需观看吧：

视频地址：【双语字幕】「线性代数的本质」合集

内容目录：

第零讲：序言

第一讲：向量究竟是什么

第二讲：线性组合、张成的空间与基

第三讲：矩阵与线性变换

第四讲：矩阵乘法与线性变换的复合

第四讲附注：三维空间中的线性变换

第五讲：行列式的意义

第六讲：逆矩阵、列空间与零空间

第六讲附注：非方阵

第七讲：点积与对偶性

第八讲上：叉积的标准介绍

第八讲下：以线性变换的眼光看叉积

第九讲：基变换

第十讲：特征向量与特征值

第十一讲：抽象向量空间

视频原作者：3Blue1Brown（可汗学院的一位教师），字幕中译：Solara570@Bilibili

作者：匿名用户

链接：https://www.zhihu.com/question/21082351/answer/126177114

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

原作者3Blue1Brown最近在Patreon上发起众筹，说如果获得足够多的资助，他就可以辞去工作，全职做这类视频，以每月两部的速度发布。计划要做的视频系列包括「微积分的本质」「概率的本质」「实分析的本质」「复分析的本质」「常微分方程的本质」等等，此外还会经常制作像「最速降线问题」「希尔伯特曲线」那样的单个视频。目前他正开始着手制作「微积分的本质」系列，凡是在Patreon上资助了他的人可以抢先看，不必等到整个系列制作完毕。

资助网址是：https://www.patreon.com/3blue1brown，诸位若有条件不妨去支持一下。最低额度只要1美元／个视频，就能优先观看今后制作的所有「XX的本质」系列视频。（刚发现，Minecraft的作者Markus Persson赫然出现在资助者名单中……）

另外还有个好消息：应B站几位字幕译者的邀请，3Blue1Brown本人已同意在B站设立官方账号：3Blue1Brown @ Bilibili，今后他在Youtube发布的精彩视频都会在B站上持续发布中文字幕版，大家可以去B站关注和支持。

编辑于 2017-02-10

1K82 条评论

收藏感谢收起

知乎用户

瑞士/滑雪教练ing/机器人科研ing/ETH Zurich/NFLS

841 人赞同了该回答

来试着回答一下这个问题吧。

1 首先讲线性代数。

既然是代数，无非都是研究量与量之间的关系。在高中代数里面：基本量是实数集里的标量，量与量的关系可以是线性的（

），也可以是非线性的（指数、幂、多项式等等）。而线性代数呢：基本量是线性空间里的向量（一个数组），基本关系是严格的线性关系。会在最后一章“二次型”里面简单讲述二次关系。

2 然后就是矩阵。

矩阵就是描述这种线性关系的参数。

2.1 我们来比较：初等代数中，

表示的是

的一种映射关系，

是描述这个关系的参数。线性代数中呢，

（

）表示什么呢？首先与初等代数一样，这个等式表示的是

的一种映射（关系），同理此处矩阵

就是描述这种关系的参数。换句话说

和

的本质是一样的。

2.2.1 那一定会有人问，为什么定义

这么复杂（加权求和）呢（远没有实数相乘这么简单）？那我想说的是，其实这是在“无损信息”下最简单的关系了！且看：我们得考虑到自变输入量

是个

维向量，那么就得把这

个维度都逐一考虑一遍吧……而且考虑到因变输出量

是个

维向量，那总得把前面那个

维（自变输入量）向量逐一考虑

次吧……这就决定了

的“信息量”一定至少得

……

2.2.2 当然一定也有人问，那为什么要用加权求和（而不用加权求积，先求和再求积等）的方式定义矩阵乘法？首先这是个线性算法（去翻线性的定义）。其次，我认为最重要的是，在非线性问题线性化后，求一阶近似的时候，一元函数：

即

其中

是

多元函数：

即

其中

是

的Jacobian。换句话说，加权求和可以表达一种边际增加的概念，这是非常有用的。

3 最后讲特征值和奇异值。

首先说明的是，特征值奇异值的定义是为了简化矩阵运算提供了一种方式，一种技巧；也是描述一个矩阵特征的特定参数，让我们从特定角度理解这个矩阵。

3.1特征值是

矩阵特有的值。说其为特征值，根据定义也好理解：定义：如果

，则说

是

的一个特征值，

是

对应的

的特征向量。换句话说，在

这个方向上，

做的事情无非是把

沿其

的方向拉长/缩短了一点（而没有一丝丝的旋转到其它方向），

就是描述这个沿着

方向上伸缩的比例。注意这里隐藏了一个重要的潜在条件：

映射的定义域和值域是相同的空间（不然无法说自变量

在其方向上通过

拉伸

倍得到因变量

），反应在大一线代里面也就是说

必须是方阵。

【西文原文中Eigenvalue Eigenvector 中的Eigen原意为“自我”，也就是说，Eigenvector是经原矩阵变换之后只向“自我方向”延伸的向量，Eigenvalue是这个“自我延伸”的倍率。所以与其翻译成“特征”，个人更愿意把它翻译成“本征”（这也是一种通俗译法）。】

那么这样，给定任意的一个向量

，我们如何求

呢？很简单，把

沿着

分解，然后分别按照各自的比例

伸缩最后再求和即可。

有人一定问，这不是折腾么！那么当你运算

的时候就发现好处了！沿着各个

的伸缩正好是

。所以，特征值在动态系统分析中是描述系统稳定性的非常重要的量，它决定了离散系统在空间内某个方向上的变化趋势（是无限扩张

？还是收缩

？还是保持不变

？），这是判断离散线性系统的重要特征。

特征值分解也就很好定义。一个可对角化的方阵

：分解为：

，

的列向量为特征向量（

）。理解为：以

为基的坐标分解变换+伸缩变换+以

为基坐标还原变换。

3.2 奇异值分解也是为了简化矩阵运算的一种方式。它和特征值变换的基本理念不同，看似繁琐一点，却能道出线性变换的一般本质。定义：任何

（而不仅仅是可对角化的方阵）的矩阵都可以如下分解：

其中

和

是正交矩阵（复数域里面是酉矩阵），

是由对角阵和零矩阵合成的矩阵。它的含义是任何

的变换可以理解为一个正交变换+伸缩变换+另一个正交变换。（正交变换可以暂时理解为 “不改变大小以及正交性”的旋转/反射等变换）这是对一般线性变换的本质的阐释。

3.3 小结：特征值变换的条件很苛刻，

必须是1方阵 2可对角化。而奇异值变换却对矩阵

没有任何要求。它阐明的是一般线性变化的本质。

-----------------------------分割线----------------------------------

才疏学浅，疏漏众多，还望达人提供意见。

2013-09-26 Ver1 初始版本。

2014-02-26 Ver2 扩展SVD（奇异值分解）部分。

2016-12-01 Ver2.1 微调了一下排版，加了英文解释部分。

2016-12-12 Ver2.2 微调了特征值分解部分。

编辑于 2017-07-06

84149 条评论

收藏感谢收起

余翔

用户标识

数学、高等数学话题的优秀回答者

49 人赞同了该回答

线性代数主要研究的是（有限维）向量空间和线性变换，矩阵不是线性代数主要研究的。

-------向量空间-------

什么是向量空间呢？数域

上向量空间就是一个集合

，里面的元素叫作向量，并且上面定义了两个运算，向量加法

和数量乘法

，加法和数乘要满足向量空间的八个公理。详细请见：向量空间。

定义了向量空间后，就可以定义生成(span)空间、线性相关和基。

向量空间

的子集

的生成空间

就是包含

作为子集的最小向量空间：

的子集

说是线性相关的，如果存在各不相同的元素

以及不全零的数

使得

。

说是线性无关的，如果它不是线性相关的。

向量空间

的一个基

就是

的一个生成集合（即

），并且是线性无关的。

前面说过线性代数主要研究的是有限维向量空间，那么什么是维数呢？

在定义维数之前，有一点细节要处理，花一点力气论证一下，就可以得到向量空间的每个基包含的元素个数是相同的。

因此我们说向量空间

有维数

如果它有一个基含有

个元素，我们说

是有限维的如果它的维数

是有限的，否则我们说

是无限维的。

-------线性变换-------

线性变换就是从向量空间到向量空间的函数，并且保持向量空间的运算。

设

是向量空间，一个从

到

的线性变换

是一个函数，并且满足下面性质：

（

保持向量加法）对任意

，

。

（

保持数量乘法）对于任何

和数

，

。

线性变换可以用矩阵来表示，为此，我们需要有序基的概念，

设

是有线性维向量空间，一个有序基是

中的有限向量序列

使得集合

是

的一个基。

设

是

的一个有序基，

是

中的向量，我们知道

有唯一的表示形式

，

我们把

叫做

相对于

的坐标，记作

。

-------线性变换的矩阵表示-------

设

是有限维向量空间，

是线性变换，

中的向量

相对于基

有坐标表示

，

因为

在

中，它相对于基

也有坐标表示

。

我们很自然地要问

和

有怎样的关系？这依赖于

相对于

和

的矩阵表示。

我们先求向量

在基

下坐标表示：

定义线性变换

相对于基

和

的矩阵表示为矩阵

稍微计算一下就可以得到

和

的关系：

。

线性变换的和、数乘和复合也可以用矩阵来表示，因为我们有下面的命题：

命题.设

是有限维向量空间有有序基

，设

和

是线性变换，设

是数，那么

。

命题. 设

是

维向量空间有有序基

，

是

维向量空间有有序基

，

是

维向量空间有有序基

，那么

。

可以看到，矩形的加法表示线性变换的和，矩阵的乘法表示线性变换的复合。我们可以表这一点说的更明白。

设

是

的实矩阵，我们定义线性变换

为

，

这里我们认为

和

中的向量是列向量。

根据上面的定义，计算一下就可以得到

设

是

的实矩阵，

是

的实矩阵，那么

。

设

是

的实矩阵，

是

的实矩阵，那么

。

编辑于 2015-01-07

492 条评论

收藏感谢收起

知乎用户

搞了一会儿密码学之后，变成机器学习苦手

53 人赞同了该回答

矩阵不是线性代数最重要的课题，是次重要的。

线性代数研究的东西，可以统一地说成是线性空间。

研究向量——向量的全体是一个线性空间。

研究线性映射——线性映射的全体是一个线性空间。

我们用8A(八个公理)定义了什么是线性空间：

要素：数域K，集合V不是空集，两个映射+: VxV->V和*: KxV->V

公理：（我把量词集中到前面了）

\exists 0 in V

\forall a, b, c in V, p, q in K

(1) a + b = b + a

(2) (a + b) + c = a + (b + c)

(3) a + 0 = a

(4) \exists d in V, a + d = 0

(5) p(a + b) = pa + pb

(6) (p + q)a = pa + qa

(7) p(qa) = (pq)a

(8) 1a = a

好了现在V是一个线性空间了。

依此我们可以定义线性空间的基、维数等等等。

线性空间的几何化例子：坐标系里面的原点、过原点的直线、过原点的平面、全空间等等等。

但是代数不是几何，代数需要研究的是结构。线性代数呢，就是研究线性空间这种结构的。

线性空间是一个很好的结构，我们可以研究线性空间到线性空间的映射，而且对这种映射加一点限制——线性。这是正比例函数的自然延拓。

如果U, V都是K上的线性空间，f: U->V，符合下面的条件：

\forall x, y in U, k in K

f(x + y) = f(x) + f(y)

f(kx) = kf(x)

那么f就是一个从U到V的线性映射。（这里特别强调一件事情：两个性质里面，左右虽然都是加法或数乘，但是由于U、V可以是不同的线性空间，所以等式左右的加法和数乘其实不同，不要混淆）

现在来点具体的例子舒服舒服：R->R、C->C之类的正比例函数是线性映射。又例如，投影映射，绕原点的旋转映射等等。

说了这么多，好像没有什么具象化的东西嘛，好像和矩阵没什么关系嘛。不然。矩阵该登场了。

对于f: U->V是K上有限维线性空间U到有限维线性空间V的线性映射，选定U、V各自的一组基u1...um, v1...vn，我们可以用m*n个K里面的数决定这个线性映射。

具体地说，就是令

f(ui) = \sum(a(i, j)v(j), j=1...n), i=1...m

知道了a(i, j)，用线性映射的线性性和基的性质，可以得到任意U中元素在f作用下的像，所以说这m*n个数决定了这个线性映射。

把这m*n个数如此排列：

a(1, 1) ... a(1, n)

...

a(m, 1) ... a(m, n)

这就是一个矩阵。

说白了，选定基，就可以用矩阵描述线性映射。

矩阵的乘法的意义极其显然——就是映射的乘法（复合）。（说到这个，最近某次考试我还因为这件事出了点洋相，不过因为保密协定，暂时不能说）

相似矩阵是什么呢？是同一个线性变换在不同基下的矩阵。所以说，对角化、化为Jordan标准形就是要寻找一组基，让这组基下这个线性变换简单一点。方阵的特征值是什么呢？就是这种“简单”的一种表现，也很自然，因为一旦有了特征值和特征向量，这个线性变换看起来就像是正比例函数了！

矩阵的合同，则是出于二次型的研究，二次型则可以用双线性形式表示。二次型看似和线性代数无关，其实骨子里还是线性的。

那矩阵的相抵（等价）呢？如果是相似，我们已经知道了。注意谈到相似的时候，矩阵是方阵，而且所描述的线性映射必须是线性变换（同一个线性空间），而且所用的基必须是同一组。去掉这两个性质，U到V的线性映射，选定U不同的基、V不同的基，都会导致这个线性映射的矩阵不同。这些矩阵是相抵的。

还有很多，在此不赘述。

发布于 2014-04-09

535 条评论

收藏感谢收起

匿名用户

34 人赞同了该回答

I trust that the answer is hidden in this book.

发布于 2014-04-13

3413 条评论

收藏感谢

匿名用户

126 人赞同了该回答

这么说吧，如果有人能给你写一个很好的答案，那他一定是花很大功夫学习了线性代数，写出来让你觉得很有道理。但你看完这些貌似很直观的理解之后，其实对你的认识和理解没有任何帮助。先认认真真学吧，没有捷径，只有学懂了才会觉得有一些直观的理解。没有深入学习的直观都是错觉。。

编辑于 2014-05-09

12626 条评论

收藏感谢

YJango

用户标识1

日本会津大学人机界面实验室博士在读

69 人赞同了该回答

什么是线性代数？

不断变化的世界使我们产生时间观念。正确描述事物状态及其不同时间下的变化至关重要。我们知道在三维空间下如何描述物体的位置。然而除了长宽高，世界上还有很多决定事物状态的因素。如决定股票价钱的因素、决定天气的因素。这些因素又该如何合理的描述？线性代数给了我们答案。线性代数 · 超智能体

线性代数是有关任意维度空间下事物状态和状态变化的规则。

矩阵

线性代数是用来描述状态和变化的，而矩阵是存储状态和变化的信息的媒介，可以分为状态（静态）和变化（动态）信息来看待。

当把矩阵以静态信息来看待时，其信息的侧重点在于状态二字。

描述一个事物的状态需要在一个选好的坐标系（什么样的向量空间）中进行，所以矩阵所包含的信息从来都是成对出现（坐标值和坐标系）。而基就是坐标系的信息，可以将其拆分出来。

当把矩阵以动态信息来看待时，其信息的侧重点在于变化二字。这时的矩阵可以看做是一个方程。

通过矩阵内所描述的变化规则从一个状态变换到另一个状态。变换可以理解为事物本身的变化，也可以理解为坐标系的变化。

矩阵乘法是什么

矩阵乘法就是变化的行为

静态信息又可以看成是动态信息的矩阵相乘后得到的状态，所以矩阵可以被分解。

秩描述的是一个矩阵内带有多少信息，秩低则信息就少。

原文

2016/11/02 更新内容：已阅读过该文的朋友，请到线性代数 · 超智能体中再看一遍关于矩阵围绕状态和变化的理解。

矩阵乘法

向量点乘

矩阵乘向量

向量乘矩阵

矩阵乘矩阵

矩阵的静态信息

坐标值与坐标系

坐标值的两种看法

矩阵的动态信息

向量空间

子空间

线性无关

张成

基基底

维度

秩

线性变换

矩阵乘法

向量点乘

下面严肃点，我是来讲线性代数的。先让我们来看一段视频，但我希望你只看一遍！PPAP洗脑全球

如果你继续读到了这句话，那么恭喜你，你抵抗住了病毒的洗脑。同时你听到了3个向量点乘。

1、I have a pen, I have an apple—->apple pen

（eq.1）

2、I have a pen, I have a pineapple—->pineapple pen

（eq.2）

3、apple pen, pineapple pen—->pen pineapple apple pen

（eq.3）

以（eq.1）举例。等式右边的第二个向量表示你有什么，右边的第一个向量表示你各拿几个，而等式的左边表示你获得了什么。从中你可以看出来：

向量点乘(dot product)是一种组合(combination)

矩阵乘向量

我们也可以把（eq.1）（eq.2）合二为一表示为（eq.4）：

I have a pen, I have an apple—->apple pen，

I have a pen, I have a pineapple—->pineapple pen

（eq.4）

这时，表示你各拿几个的向量变成了两行（两组），也就成了矩阵（向量是只有一行或一列的矩阵）。

表示你各拿几个的一个向量也叫一组权重(weights)。

在

中，第一个1对应着apple，第二个0对应着pineapple，第三个1对应着pen，我们不可以随意调换位置。所以，

向量是有顺序的一组数字，每个数字都是该向量的一个因素(element)

因素横着排列的向量叫做行向量(row vector)，因素竖着排列的向量叫做列向量(column vector)

到这里我们需要更具体的描述一下第一个结论。向量点乘是一种组合，但

向量点乘向量可以是列向量中各个因素的一个组合

上式（eq.4）可分两步计算：

计算第一行权重得到的组合apple pen后，放到了第一行

计算第二行权重得到的组合pineapple pen后，放到了第二行

行成的依然有顺序，仍然是一个向量。比较向量点乘向量，我们可以看出

矩阵乘向量可以是列向量中各个因素的多个有顺序的组合

向量乘矩阵

然而形成组合的成分并不一定非要是向量中的各个元素，也可以是不同向量之间的组合。我们可以把（eq.1）（eq.2）（eq.3）改写成（eq.5）（eq.6）：

（eq.5）

（eq.6）

在（eq.5）等式右侧的矩阵是由两个行向量组成的。矩阵中，第一个行向量表示怪蜀黍两次组合中分别先拿什么，第二个行向量表示两次组合中分别后拿什么。等式右侧的权重（行向量）的第一个因素对应着矩阵中第一个行向量的个数，第二个因素表示右侧第二个行向量的个数。这样保持矩阵中每个行向量内部因素的比例，完成矩阵内向量与向量之间的组合。

向量乘矩阵可以是矩阵中各个行向量的多个有顺序的组合

而向量中的每个因素都可以当成是因素个数为一个的向量，也再次解释了为什么，向量可以看成是矩阵。

在（eq.6）中，你会发现，要形成组合的向量被拿到了乘法点(dot)的左边，而权重被拿到了右边。因为当行向量的因素作为组合成分时，乘法点右侧的矩阵（向量）装有着权重信息。效果是拿一个penpineapple和一个applepen形成组合。

从中你可以看出矩阵乘法并不满足乘法交换律，因为交换了两个矩阵的位置，就交换了权重与要形成组合的向量的位置。

矩阵乘法不满足乘法交换律：commutative law: AB =! BA

矩阵乘矩阵

如果怪蜀黍跳了两遍舞蹈。第二遍跳舞时，他在两次组合时，后一次拿的东西都是都拿两个，那么我们就可以把等式右侧的行向量变成两个行向量，也就形成了一个矩阵。

那怪蜀黍在唱第二遍时，就要唱：

I have a pen. I have two apples. 2-Apples-pen!

I have a pen. I have two pineapples. 2-Pineapples-pen!

那该蜀黍就有卖水果的嫌疑，每次都拿两个水果。

至此你看到了我用的是2*pineapple +pen方式去形成组合。也就是只有乘法来控制数量，加法来组合不同向量。这样的组合方式才是线性代数讨论的组合，即线性组合。所以我们所有概括的结论中，所有组合前面都要加上线性二字。同时乘法所乘的数属于什么数要事先规定好（经常被规定为是实数

，也有虚数域）。不过这还没有结束，严谨性是数学的特点。我上文所说的“加法”“乘法”也只不过是一个名字而已。它们到底指的是什么运算，遵循什么样的规则。然后当你看线性代数教材的时候，你就会发现这8条规则。

There is a unique “zero vector” such that

for all x.

For each x there is a unique vector

such that

然而你不需要去记它们。你只需要知道，他们是用于描述和约束在线性代数中的加法，乘法的运算。特别要注意的是，这些运算都有一个原点（0），为了允许正负的出现。

线性组合：一组向量乘上各自对应的一个标量后再相加所形成的组合。（满足上述对乘法、加法的规则）

当我们再用(m by n)，即m行n列的方式去描述一个矩阵的形状(shape)时，你就得到了矩阵的第一种描述：

矩阵的静态信息

坐标值与坐标系：

矩阵所包含的信息从来都是成对出现，拿向量

举例来说，这个向量并没有被赋予任何数值。但你已经确定了你要在apple的数量和pen的数量的两个因素（两个维度）下描述你的数据。换句话说，你已规定好你的坐标系。所以当你写出任何具有实际数值的向量，例如

时，他们的坐标系（二维向量空间）和坐标值就同时被确定了。它实际上是

和

的缩写。二者无法分割。即使是

，虽然我没有再pen，apple前面写具体数字。但依然包含所有因素间的比例相同的隐含信息。而调换2和1的顺序同时也表示坐标轴之间的调换。

坐标值的两种看法：

单单考虑坐标值时，有两种角度去理解矩阵所包含的静态信息。

矩阵的静态坐标值信息：

（1）若干个维度相同的要形成组合的向量信息

（2）若干组维度相同的权重信息

他们本质都是向量，然而（2）中所指的向量（或叫权重）是用于控制每个向量的数量（scale），而（1）中的所指的向量是要通过乘法与加法的线性组合形成新向量的向量。

拿矩阵来说，你可以理解成该矩阵包含了两个行向量，也可以理解为包含了两组权重；同时，用列向量的方式也同样可以理解成向量和权重。

矩阵的动态信息

在一个矩阵内，你把矩阵内的向量理解为向量或权重都可以。但是当两个矩阵进行矩阵乘法时，一旦选择以权重信息理解其中一个矩阵，另一个矩阵的信息就会被瞬间确定为要形成组合的向量（量子力学的味道）。

举例来说，它的实际数学表达应该是：

，即便是都换成了数字，其物理意义任然存在，始终并未丢失。但也可以被理解为其他的物理意义。我会在

与

二者之间进行切换，他们表示同一个矩阵。

当我把矩阵

看成是两组行向量的权重时，后一个矩阵的两个行向量

和

就瞬间被赋予了要形成组合的向量的观察方式。

当我把矩阵

看成是两组列向量的权重时，前一个矩阵的两个列向量

和

就瞬间被赋予了要形成组合的向量的观察方式。

矩阵的动态信息，两个矩阵相乘A⋅B 时，

当把前者矩阵(A)中行向量理解成若干组权重，后者矩阵(B)中的行向量就是要形成组合的成分。

http://weibo.cn/qr/userinfo?uid=5288598930(二维码自动识别)

同样的两个矩阵相乘

当把后者矩阵(B)中列向量理解成若干组权重，前者矩阵(A)中的列向量就是要形成组合的成分。

http://weibo.cn/qr/userinfo?uid=5288598930(二维码自动识别)

注意对应行向量与列向量。

请回想线性组合的描述（一组向量乘上各自对应的一个标量后再相加所形成的组合），这是因为向量的维度和权重的维度要一一对应。所以，

矩阵A(m by n)和矩阵B(p by q)能够做乘法的条件是n = p

向量空间

很多线性代数教材所引入的第一个概念就是线性空间（linear space）。可见它的地位。虽然它有些抽象，但是却是自然而然推演出来的一个概念。

空间的本质是集合。而且是一个能够容纳所有你要描述内容的集合。

在具体讨论之前先要对上句话中“你要描述的内容”进行进一步说明。

从如何理解线性代数这四个字开始。首先我们已经知道了什么是线性（那8个条件约束的加法和乘法）。那什么是代数？意思是指你可以把任何概念都代入其中。

可以怪蜀黍手中的水果和笔换成盆和大菠萝PPAP河南话版。也可以换成任何宇宙上有的物体。然而不仅仅是物体，甚至可以是一个抽象的概念。我个人最喜欢的描述是：向量空间是描述状态(state)的线性空间。再加上之前的约束，于是我们就有了

向量空间是能够容纳所有线性组合的状态空间

那什么样的空间（所有状态的集合）能够容纳所有的线性组合？

如果说，我现在想要描述的你的两个状态（下图中的行向位置，和纵向位置），向量的维度就是二维。那么一个大圆盘够不够容纳所有的线性组合？答案是不够。

因为线性组合是一组向量乘上各自对应的一个标量后再相加所形成的组合，而这个标量是实数域的时候，由于实数域无线延伸，那么乘以标量后的状态也会无限延伸。所以向量空间一定是各个维度都像实数轴一样可以无线延伸。最终你得到的将不会是一维下的线段，二维下的圆盘。而一定是一维下的无限延伸的直线，二维下的无限延伸的平面。

向量空间的基本特点是各个维度都可以无限延伸。

我之所以用状态二字，是因为刚才的两个维度，我可以用于描述你的速度和体温。这时，这两个维度所展开的依然是一个平面，但却又不是描述位置的平面。

子空间

子空间（subspace）可以被想成是向量空间内的空间，同样要满足能够容纳线性组合的条件

那么最小的子空间是什么？只有一个状态的空间（集合）。而这个状态不是其他状态，就是0。只有这样才可以在乘以完一个标量后依然不会跑出空间外部。（因为跑出去了，我们就不得不扩大空间来容纳它）。其次空集可不可以是向量空间？不可以，空集是没有任何元素的集合，既然什么状态都没有，又怎么能够容纳线性组合。

最小的向量空间是只包含零向量的空间

假如上图的圆盘是一个无线延伸的平面，那么这个平面的子空间就是那个平面上所有直线吗？不是，8个运算规则中明确规定了，一定要有原点，这样才可以包含正负。所以这个平面的子空间是所有过原点的直线，并且包括中心的那个原点自己所组成的最小子空间，同时也包括这个平面自身（最大的子空间）

线性无关

s你会发现，在怪蜀黍的例子中，当要把可以把（eq.1）（eq.2）合二为一表示为（eq.4）时，是这个样子：

（eq.4）

（eq.4）最右侧的向量并不是

4个维度。而是三个。因为pen 和pen是一个东西。我们想用的是若干个毫不相关的因素去描述状态。这里的毫不相关是在线性空间下的毫不相关，所以叫做线性无关。那么当我们要描述的状态是由向量来描述时怎么办？我们知道判断两个向量是否线性无关是，可以看他是否在空间下平行。但怎么判断几个向量之间（不一定是两个）是否线性无关？我们需要可靠的依据。这也是数学为什么要证明，它要让使用者知道某个性质在什么条件下适用，什么条件下又不适用。

线性无关（linearly independent）: 当

表示权重，

表示向量时，

只发生在当

全都等于零时。

换句话说，这些向量不可以通过线性组合形成彼此。形成彼此的情况只能是他们都是零向量。

张成

明白了线性无关后，张成（spanning）就十分容易了，接下来要注意的是词的属性和关联词。

张成（spanning）是一个动词，而动词的主语是一组向量（a set of vectors）。描述的是一组向量通过线性组合所能形成子空间。是个动词，描述的内容并不是形成的这个空间，而是形成的这个行为。

，就可以看成是4个向量，这4个向量，可以张成一个三维空间。（因为有两维线性相关，所以并不能张成4维）

基（基底）

基底也是建立在张成的基础上理解的。

一个向量空间的一个基底（A basis for a vector space V）是一串有顺序的向量（a sequence of vectors），满足：

A、向量之间彼此线性无关（不可多余）

B、这些向量可以张成向量空间V （不可过少）

换句话说，刚刚好可以张成向量空间V的一串向量是该向量空间V的一个基底

基底是一个类似people的复数名词，是从属于某个空间的，而不是矩阵，也不是向量。

维度

一个向量空间可以有无数个基底。但每个基底所包含的向量的个数（the number of vectors in every basis）是一个空间的维度。注意，维度是空间的概念，而不是描述一个具体的向量。人们常说的n维向量实际是指n维向量空间内的向量，由于在讨论时并未给向量指定任何实际的数值，所以可以是任何值，可以张成整个空间。所以其真正描述的依旧是一个空间。并且，选择的维度是一个站在观察者角度，希望在某个向量空间下可以尽可能的描述一个物体的状态而选择的，并不一定是被描述者真实处在的空间。数学就是这么“拐外抹角”的去描述一个概念，不过确实非常有必要。但若是你觉得理解起来有困难。就简单记住：

互不相关的因素的个数是一个向量空间的维度。

秩

秩（rank）是矩阵的概念。指的是一个矩阵的所有列向量所能张成的空间的维度。

矩阵的所有列向量所张成的空间叫做列空间（column space）

矩阵的所有行向量所张成的空间叫做行空间（row space）

一个矩阵的列空间的维度是这个矩阵的秩，同时也等于该矩阵行空间的维度

秩是用于描述矩阵的包含的信息的

转置一个矩阵可以理解为调换一个矩阵的行空间与列空间。

单位矩阵可以被理解为行空间与列空间相同。

线性变换

线性变换（linear transformation）可以说是最最重要的概念了。你可以忘记我上面描述的所有内容，但不可以不深刻理解线性变换。下面是关于什么叫变换。由于概念很重要，我先不用逗比例子来解释。而用比较抽象的描述。

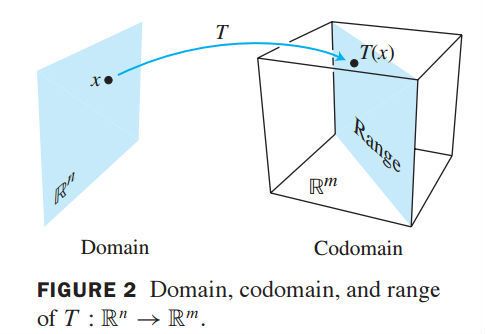
一个从n维实数域（

）到m维实数域（

）的变换（transformation or mapping or function）

是将n维实数域（

）空间下任意一个向量

转换成为在m维实数域（

）空间下对应向量

其中n维实数域（

）空间叫做变换T的domain，m维实数域（

）的空间叫做该变换的codomain。

向量

叫做向量

的image（变换T行为下的）

所有image组成的集合叫做变换

的range

而线性变换是是指线性规则所造成的变换，

是由一个矩阵

来实现的。此时你就会看到无处不在的式子：

：列向量

左乘一个矩阵

后得到列向量

（eq.4）举例来说，

是三维空间的向量（即

的domain是三维），而经过线性变换后，变成了二维空间的向量

（即

的codomain是二维）。

矩阵

可以被理解成一个函数(function)，将三维空间下的每个向量投到二维空间下。

也可以理解为x经由一个动因

，使其状态发生了改变。

同时也是深层神经网络每层变换中的核心：

在机器学习中你会你会需要构架一个虚拟的世界，并选择合适的、用于描述某个事物状态的各种因素。

线性代数是有关如何构架“世界”的学问。矩阵又是存储着所架构的世界的信息的媒介。

举一个小小的例子，比如你想通过温度，气候，湿度，当天时间，海拔，经度，纬度等信息来描述天气状况，从而进行预测是否会下雨。你如何合理的选择这些信息？你如何知道这些信息，海拔和气候如是否相关，是否重复？如果重复，那么你又是否可以减少某个信息？判断的准则又是什么？

数学讲的是我刚才所描述的内容的纯粹的结构关系。请你忘记我给你举得怪蜀黍例子，抓住“逻辑框架”。当你可以把这种关系应用在任何符合该结构关系的现实现象中时，你就算是精通了如何应用数学。

线性代数的内容十分庞大，行列式，特征向量，奇异值分解等你也会经常用到。然而我的描述就到此为止，我无法涵盖所有内容。写这篇文章只是希望能够用你脑中已有的概念帮助你构建一个对线性代数模糊的认识。当你今后用到线性代数时，再不断的加深和更正此刻的理解。

编辑于 2016-12-18

699 条评论

收藏感谢收起

JohnnyLee

搬得一手好板儿砖

26 人赞同了该回答

同济的线性代数教程我当年大二觉得自己学的很透，每一章课后习题基本也都做完了，当时觉得自己很牛逼，考试的时候应该也是全年级第一吧97。然而！然而！当我来到美国后，我发现我特么跟傻逼一样，大部分的线性代数我居然看不懂，就比如连特么多维高斯分布里面居然会带着矩阵，这个公式的物理意义和怎么跟一维高斯分布联系起来我一点都不知道。所以我又用了不到一年的时间去听了youtube上MIT的视频，之后还修了我们学校数学系的应用线性代数，拿了A+，但因为是本科课所以课上要求也不高。综上，我觉得老师和材料很重要。一般的国内的大学（top10除外）教的线性代数的知识仅仅为工业界需要用的20%-30%，而美国课上所交为70%-80%，国内老师的作业难度为15%左右，考试难度为15%；而美国作业难度接近90%，考试难度50%-70%。以上均为我个人经历，大家只做个参考吧。中国讲课偏重计算，因为老师的学术水平或讲课技巧不够，还有教材水平稍低，毕竟大部分老师没有参与过类似matlab顶级实验室的线性代数运算函数的设计，没有什么高端的经验，所以有可能老师自己都不知道知识用来干什么的，知识最重要的点永远不在计算，因为计算可以说完全是体力输出，我们学习的重点应该永远在于思维和素质的培养。就像MIT Gilbert Strang讲的线性代数，我觉得作为一个本科生，如果你能把一个2x2的矩阵的性质搞得差不多透，你的本科的线性代数就是成功的了，已经为你不论在工业界还是学术界都打下了坚实的基础。

我下面给出自己的愚见，你可以看看自己是否能回答上我的问题。

1. AB=C 这个式子可以有几种计算方法实现（我现在知道4种，我本科只学了一种，后面三种你不懂可能就不容易理解向量空间和SVD)

2. 任意一个矩阵A，它的四大子空间col space, row space, null space, left null space分别是什么维度，如何去求它们的基底，代表什么物理意义，各个子空间什么关系，怎么应用

东西太多了，我就先说这两个最基本的吧。希望你有所收获。

编辑于 2016-11-05

2620 条评论

收藏感谢

知乎用户

经济研究汪

7 人赞同了该回答

读完Linear Algebra Done Right就行

发布于 2014-08-08

7添加评论

收藏感谢

知乎用户

8 人赞同了该回答

《理解矩阵》老三篇以矩阵为线代的中心，是错误的和业余的（作者孟岩本来也就不是数学专业人士）。可以参考蓝以中的《高等代数简明教程》前言。

1、代数的基本研究对象应当是各类代数系统及其相互关系（态射），对于线性代数，其核心是线性映射（变换）。扩展出来的关系有：线性变换和双线性函数的关系，双线性函数和内积空间的关系，线性空间的应用（向量空间、多项式空间、线性方程组）

2、对有限维线性空间，取定一组基后，可以把问题转换为具体的矩阵论课题。但对无限维线性空间以至一般代数系统（群、环、模等），则不可能。所以矩阵论不能全面反映代数学的基本思想、方法，它不是线性代数（高等代数）的主线，不应占太大分量，冲击主线

3、处理矩阵论的核心课题，对于抽象代数很熟练的读者，无疑会看清其捷径的。（N.Jacobson《抽象代数学第二卷线性代数》）

编辑于 2015-09-10

82 条评论

收藏感谢

唐平

航天灌水，业余PM，初涉CV，主业刷知乎

15 人赞同了该回答

好好看一遍这本书。

线性代数及其应用 (豆瓣)

真正做到每一个重要概念都有对应的来由，每一章都有相关领域的应用范例。

学过线性代数、甚至用过好多年了再回头来翻也可，直接拿来入门也可。

发布于 2014-06-30

153 条评论

收藏感谢

JX Consp

朱门酒肉臭，路有克苏鲁

1 人赞同了该回答

【转】随记：我们需要怎样的数学教育？

看这个

其实矩阵想要的就是一个简单的R^m到R^n的映射

秩就是保证是在R^n上而不是R^n上的一个sub space(其实我不知道这东西的英文或者中文怎么说所以我随意扯了一个名词)

特征值和SVD放在一起比较好，就是把线性映射分解成一个旋转镜像和一个拉伸

收工了，现在你可以去学学统计学看看线性代数有什么应用了（之所以不说量子或者电动是因为这两科我不敢推荐textbooks，因为学得时候没有好好看textbooks

编辑于 2014-11-05

11 条评论

收藏感谢

aresmiki

Phd Southwest Jiaotong University

5 人赞同了该回答

知乎专栏

编辑于 2016-11-23

5添加评论

收藏感谢收起

半梦半醒

热爱钻研。追求完美。

9 人赞同了该回答

第一次回答问题。努力尝试讲得明白点。若有不妥请指正。我对矩阵这么理解的。首先还原矩阵的物理意义。我把矩阵看作方程组的系数。那么，一个n个变量的方程，最多有n个独立的行，再多就是冗余了。所以我把秩看作方程组有意义的方程的个数，也就是一种信息的度量。

发布于 2014-11-06

96 条评论

收藏感谢

知乎用户

学之。

17 人赞同了该回答

要谈理解，必须讲范畴，也就是你要应用在哪里。

比如“红色”在电工的世界里是火线，在工业设计者的王国里是危险，在物理学世界里是波长630到750纳米的可见光，在画家眼中是激情……

弄混了范畴谈直观是危险的，比如这篇文章看上去很好，但是如果你以后学习现代控制论的时候拿矩阵当成空间里的变换，那无异于让画家去用波长来理解红色。用普通课本上的线性方程组去理解就会非常恰当……

发布于 2013-05-19

173 条评论

收藏感谢

匿名用户

9 人赞同了该回答

个人的经验是，把大部分重要的定理自己独立证出来，基本上你就懂了。

发布于 2014-05-12

93 条评论

收藏感谢

张帅

以前习惯性点赞，现在习惯性反对+没有帮助

37 人赞同了该回答

我是一名大四狗，学习线性代数也不过是一本同济五版的教材，有自己的一些理解，但是不敢说完全正确。

Action

我开始以为矩阵是为了把线性方程组的系数抽取出来，方便方程组化简和求解，后来发现矩阵的用处不止如此，不然就不会写一本书了。

矩阵可以方便的用来表示线性空间，一个简单的二维数阵，就可以表示成n维线性空间。

一个毫无意义的有序数阵，我们赋予它意义，他就可以表示成一个空间。那为什么要这么做呢？这是因为矩阵的运算可以表示线性空间的变换。以向量举例，我们求两个向量相加，可以让(x1，y1)和(x2，y2)相加，而不必真的在图上画出来这个相加后的向量。到三维空间我们就画不出来了，因为二维空间中的向量不能表示三维空间中的向量。同样，n大于3以上维度的空间中的向量我们不但不方便表示，甚至根本实现不了，但是矩阵可以帮助我们表示出来。一个3x3的矩阵，我们把他分成三列，就得到三个三维的列向量，同样4阶方阵中包含了4个4维向量。

--------------------------------------------------------------------------------------------------------------------------------------------

为了直观理解，下面全部用二维向量举例。

平面内引入直角坐标系之后，二维空间内所有的向量都可以用两个基向量i=(1,0)和j=(0,1)的线性组合来表示，例如a=(4,6)，可以表示为a=4i+6j。

但是也可以由i=(2,0)和j=(0,2)两个向量来表示，例如a=2i+3j。

还可以由i=(1,1)和j=(1,-1)来表示，例如a=5i-1j。

或者由i=(1,0)和j=(1,-1)表示，例如a=10i-6j。

在1的基础上，我们还可以将a表示为i=(1,0),j=(0,1),k=(1,1)三个向量的线性组合，也就是a=4i+6j+0k或者a=0i+2j+4k或者a=2i+4j+2k等等等等我举不完了。这其中k=i+j。

通过上面的举例我们可以总结出几条。

由5点到4点，将多余的基向量k去掉，得到最大线性无关向量组。

由4点到3点，将两个基向量的夹角变成直角，实现正交化。

由3点到2点，将构成正交的两个基向量旋转，使其与坐标轴重合，实现对角化。

由2点到1点，通过伸缩将两个基向量的长度变成单位长度，实现规范化。

通过上面的几个步骤，我们可以看出，任何一组向量构成的坐标系，都可以通过化简，正交，对角，规范的过程，将任何乱七八糟莫名其妙的坐标系变换成笛卡尔坐标系。那这么做有什么用呢？到这里我开了一下脑洞：

假如说，平面内有两个椭圆，将直角坐标系的原点放在一个椭圆的长轴和短轴交点处，这样就可以得到这个椭圆的标准方程，就是高中课本上那个。由于这两个椭圆的位置相对，这样一来另一个椭圆的位置也就定下来了，可惜很难看，长得很歪，很难用方程表示。这时就可以以这个椭圆为原点再建立一个坐标系，并且在这个坐标系下用标准方程表示出来，这样两个椭圆都有了方程来表示，问题就化简为了两个坐标系之间的关系，这时再用矩阵来运算就好了。可惜这里不能画矩阵，关于矩阵的好多问题都不能解释。

BTW，上面列举的例子都是同维度内的问题，关于升维和降维的问题其实关系到求矩阵的秩，以及线性方程组有解无解多解的问题。

----------------------------------------------------------------------------------------------------------------------------------------

关于特征向量和特征值我还没想到，想到我再告诉你

编辑于 2014-12-01

3713 条评论

收藏感谢收起

马冲

4 人赞同了该回答

请参考：An Intuitive Guide to Linear Algebra

发布于 2014-05-08

4添加评论

收藏感谢

David

电气工程师

5 人赞同了该回答

一条直线，由一个一维向量与一个系数相乘即可表达。

一个平面，由两个相互独立的二维向量与两个系数相乘即可表达。

一个三维空间，由三个相互独立的三维向量与三个系数相乘即可表达。

一个四维空间，由四个相互独立的四维向量与四个系数相乘即可表达。

一个五维空间，……%￥#

向量A与向量B相互独立，即A不能用B与一个系数k相乘得到。

系数k属于实数。

矩阵的秩就是相互独立的向量的个数。不知道谁起的名字，抽向又难懂。

矩阵的列数就是向量的维数。

仅当维数等于相互独立的向量的个数时才能表达一个完整的维度空间。

当然四个相互独立的四维向量也能表达三维，二维，一维空间。

四个相互独立的四维向量表达三维空间必有一个向量为0向量。

四个相互独立的四维现量表达二维空间必有二个向量为0向量。

四个相互独立的四维现量表达一维空间必有三个向量为0向量。

1000

0100

0010

0001

四维空间里四个相互独立的单位向量，正交向量，相互垂直。

任意两个可组成一个平面，就是三个不平行平面。

看了孟岩的《理解矩阵》，认为线性变换不是运动，而是在不同方向的投影。

编辑于 2016-05-05

5添加评论

收藏感谢

Cheung Tim

程序员

18 人赞同了该回答

哎，做到直观？

如果中学生进入大学，怎么让别人给线性代数你讲得直观，也没有办法直观起来，都是莫名其妙，一头雾水。

如果学了群论，学了矩阵论，或者看了现代控制理论，或者量子力学……怎么看线性代数都会觉得真直观，真简单，恨不得用再少些在抽象点的话来描述，这样才够本质。

这个过渡过程，除非天赋异常，只有一个绝杀办法，学什么都能直观起来，而这早已是学数学人的共识：

大量做题，大量思考。

《理解矩阵》以前也看过，啰嗦半天，还不如好好做一题体会深刻。

当你学会了更加抽象的数学，或者学回了大量的线性代数的理论（量子力学，哪怕第一章）上或者工程上的应用（机器视觉、现代控制理论等等），你再回头看看线性代数。

发布于 2014-05-08

184 条评论

收藏感谢

风行

阅读，思考，觉悟，传播。

4 人赞同了该回答

我是传统数学教育的受害者，也是追求各种直观理解的受害者，对于物理以及数学，直观理解是最初的进入这些学科门径，是为了分解这些学科作为一种复杂科学的基本难度而采用的一种理解方法，但是过于依赖这种理解，结果会成为一种障碍而最终无力克服。但是，复杂科学的抽象性，在一开始就被呈现在大多数初学者面前时，也会呈现出一种障碍，如果不能克服这种障碍，甚至连入门都没有可能，就更谈不上以后去用抽象的方法去理解这些学科的复杂性了。所以说对于一些数学原理的直观性的理解方法，在学习过程中还是很必要，或者很有用的方法。

线性代数中所谓线性，我在上大学的时候就很费解，总是是对线性这个词过敏或者免疫，导致很严重的概念混乱，其实后来是通过非线性来直观理解线性的，所谓非线性，举个例子，如果一个放大器，比如三极管，实际三极管的工作电压或者集电极与发射级之间的耐压不是理想的数值，而是一个有限的值，所以超过这个电压，三极管就会被击穿而损坏，所以一般三极管的电压都是由直流电源提供的一个低于耐压值之下的安全范围的恒定电压，这样，当三极管工作的时候，就有线性区和非线性区，到了输出值大于电源电压以后，实际的输出值就不会再随着输入电压的变化而变化，结果就叫饱和了，所以我理解所谓线性就是所谓直线性或者曲线性，用函数理解，就是一次函数的直线性，二次函数的线性，三次，直到n次函数等等，所谓非线性就是说，超出函数表达式以外的次元函数的系数方式的表达，比如饱和的状态，所以计算机的0和1的信号，就是一种没有利用三极管的线性区的工作方式的一种应用，而这种应用有很大的好处，一个三极管如果只工作导通或者截止这两种状态下，结果，这个三极管的功耗会最小，这个很有用，就好比晶闸管的工作模式一样，器件的耗散功率会大幅度减小。所以说对一个线性理解，如果借助了直观就很快可以进入这个概念，但是如果直接抽象，这对一些人还是比较困难的，因为我们在学习过程中，往往有些人不能完全记住整个学习过程一路下来所有的最初的那些定义，或者理解之前一开始一路上所有的那些定义，以至于对于数学这个严格的具有数理逻辑的学科，往往会发生，一个环节的阻碍而导致之后的一切混乱。

然后说线性代数，其实我在上学的时候，对于线性代数也是一头雾水，原因就是上述的因素导致的，线性代数是讲的有关数理空间的问题，那必然跟空间有关，但是我们人类生活的现实世界本身是一个三维空间，所谓三维空间就是我们只能建立一个上下、前后、左右这三个方向的互相垂直的一个坐标系，在这个三维的立体坐标中，每个方向都是相互独立的，也是所谓唯一独立，这是汉字唯这个概念的直观解释，唯就是唯一，在X轴上的量的变化，在另外两个坐标形成的平面上的投影永远就是一个零点或者原点，这个轴上变量不能在正交平面上形成影响，这就是唯的意思，唯就是唯独，唯一的意思。是独立的意思。所谓三维空间，就是现实空间中，存在三个相互独立的方向，在这个方向上的函数的自变量与另外两个轴相互独立，这很容易理解，因为我们就生活在现实的三维空间中，这个时候还有一个量出现了，这个量是时间，而时间对于空间而言，也是一个独立的轴，结果往往我们说人是生活在四维时空之中的，但是这个时间轴却不能在现实的几何空间被直观表达，但是可以理解。这样就出现了虚拟空间的概念。

线性代数就是这种虚拟空间表示的一种方式，实际上是数理空间的概念，只不过这种空间所要表达的是一系列线性方程的系数（也就是不同次元前面的常数）形成的一个方阵或者矩阵。对于这个矩阵，如果有维度这个概念，就请参考三维空间的直观理解。对于秩这个概念，应当是用来判断这些线性方程组是否有解的的一个量，秩的含义应当是从秩序这个词来的，如果一个方程组有解就应当是表明了一个有秩序的数理，否则就是混乱，所以用这个角度理解其中的概念就比较容易。

另外，由于计算机的发展，计算机取代人工可以进行大量的数值计算，这种计算中，线性代数就有无比强大的优势，只要设定了计算规则，计算机就可以对这些十分规则的数字或者数据可进行高速的大量的处理，而线性代数的矩阵就是各种运算的一些标准化的模型，也是数据库的基本形式。

这是我现在的理解，当年上大学的时候也很混乱，就是找不到一个人能够给我一个解释，以至于我这样一个爱钻牛角尖的人，同时又是一个浮躁的人，同时又是一个最细不很踏实的人，最终不能很好的理解这些知识，真是很遗憾。

发布于 2016-10-13

4添加评论

收藏感谢收起

匿名用户

6 人赞同了该回答

http://www.zhihu.com/question/20507061

http://www.zhihu.com/question/19863743

http://www.zhihu.com/question/20534668

首先希望你提问前先搜索，其次希望你学会自己思考。

理解了矩阵，你提到的其他概念应该自己领悟出来，不能什么都指望别人手把手教。

编辑于 2013-05-19

6添加评论

收藏感谢

做游戏的老G

移动游戏开发，微信公众号：laogdexiaowu

2 人赞同了该回答

线性代数研究的是线性空间问题，只要这个问题域和解在线性空间中，就能使用线性代数。

从图形学角度说，线性代数强大的地方有很多：

1.齐次空间的丰富含义，仿射矩阵，升降维度等等

2.矩阵变换在算法推导中的应用，很多数学推导回归线性空间时，采用矩阵表达式

3.向量是数据，矩阵封装了对向量的变换。通过矩阵乘法，你可以把数据和操作看成一类东西，编程中也有这种思想

4.强大的计算工具，同时计算所有维度的解，跟程序中的POD配合很好

还有很多很多……

发布于 2014-11-05

2添加评论

收藏感谢

文刀流

球还我，回家了

2 人赞同了该回答

理论与实际结合，比如线性代数与OpenGL结合，矩阵的各种公式都能在图形学里找到对应关系，理解起来也更简单

发布于 2014-05-08

2添加评论

收藏感谢

知乎用户

数据分析爱好者。博客：http://mengqi92.github.io

2 人赞同了该回答

同样推荐《线性代数及其应用》，我觉得这本书除了有许多插图，方便我们直观理解外，更重要的是穿插了许多现实生活中的应用。

我现在一边看这本书一边做总结，发表在了我的博客上，题主有兴趣可以看一下：

线性代数拾遗

比如关于矩阵的秩，我们可以通过列空间来理解。列空间就是把 mxn 的矩阵按列拆分成 n 个列向量，只有各列线性无关时，这 n 个列才能张成 n 维空间，这时就说这个矩阵的秩为 n；而假如这里面有 1 列和其他某列线性相关，那么这 n 个列就只能张成 n−1 维空间，这个矩阵的秩就是 n−1；也就是说， 矩阵的秩说明了这个矩阵的列向量最多能张成多少维。

比如下面这个图：

A=[a1 a2 a3]，由于有两个向量线性相关，导致 3 个列向量只能张成 2 维，因此 A 的秩为 2。A 虽然是一个三维矩阵，但它其实只是一个二维平面（就像现实空间的一张纸），算是“特殊情况”，不是“真正”的三维矩阵。除掉这些“特殊情况”，也就是“真正”的三维矩阵它的秩应该是满的（满秩）。

上面“特殊情况”和“真正”都是我自己造的词，学术上把特殊情况称为“奇异矩阵”，“真正”能撑满空间的矩阵称为“非奇异矩阵”（满秩矩阵）。

还有，为了解释方便，我这里都用“矩阵”这个词来描述了，实际上还要区分是不是“方阵”。

这部分关于秩的讨论在我的这篇文章里有提到线性代数拾遗（二）：线性方程组的解集及其几何意义

编辑于 2016-09-20

25 条评论

收藏感谢收起

匿名用户

1 人赞同了该回答

整数维上面的游戏。。。

我能想到的最为简单的解释。。。

发布于 2014-11-05

11 条评论

收藏感谢

匿名用户

1 人赞同了该回答

建议参考《线性代数的几何意义》一书。

发布于 2015-09-20

1添加评论

收藏感谢

正午

不会玩游戏的程序员

1 人赞同了该回答

从个人经验来说，多去理解，线性空间，线性变换，向量这些基本概念，再去寻找各种运算有什么意义。为什么呢？数学某种意义上来说是现实的抽象，抽象过程的第一步就是建立与现实对应的数学概念，然后在进一步研究这些性质。或许数学的发现过程并不是这样的，可能是先发现了某个性质后有概念，但是我们理解的时候一定要深刻的理解概念。

具体到这个问题，我们看向量吧，基本上很多事物都能抽象成向量，比如说一篇文章可以用词做维度词频做权重的向量，对于一个人也可以用同样的方法抽象成向量，比如身高，体重就能大致描述一个人的体型，如果你要研究的问题是人的体型相似性就可以转化为向量的问题，向量有个很重要的意义就是几何意义，两维，三维的时候很好理解因为我们能很形象的想象出来。高维空间可能就会对应上些超平面之类，但是本质上和低维是一个道理。比如线性变换就是在对矩阵的行向量，或列向量平移，拉伸（已经不能确定有没旋转了）。再说个栗子，svd分解貌似也就是在寻找一个能最大程度上代表原空间的低维空间。至于具体细节公式就看看书，或者深刻理解一些基本定理之后这些东西都可以自行推出来的吧！（显然我还没到这境界）

总之，数学是抽象的，把他与形象相结合是理解它的最好方法，也是将数学应用到现实世界的唯一途径。

发布于 2015-09-11

1添加评论

收藏感谢

百年孤独

大学毕业生

线性代数有一种玩消消乐和转魔方的感觉，自己领悟

发布于 2017-09-22

0添加评论

收藏感谢

宋好人

这是梦想成为设计师的男人。

就是向量。。

发布于 2016-10-14

0添加评论

收藏感谢

Cloud.Z

Change is my style！

有本许以超的《线性代数和矩阵论》，看了你就懂了

发布于 2016-10-13

0添加评论

收藏感谢

Karry Zhao

数据咨询

在不同维度之间旋转跳跃。

这是我现在理解到的层面。

发布于 2016-10-13

0添加评论

收藏感谢

尹世远

菜鸟/电子科大

自己去找了找题主说的那篇文章

贴个地址出来吼吼吼

理解矩阵

一http://m.blog.csdn.net/blog/myan/647511

二http://m.blog.csdn.net/blog/myan/649018

三http://m.blog.csdn.net/blog/myan/1865397

发布于 2016-01-03

0添加评论

收藏感谢

禹zh

矩阵（非奇异矩阵，满秩方阵），是一个向量，也是一种变化。我是这么瞎琢磨的。

发布于 2015-06-03

0添加评论

收藏感谢

王名扬

就是线性变换呗，可以认为它是三维图形的仿射变换及退化。高维情况可类比

2018-01-31 转载知乎： 如何直观理解矩阵和线性代数？

你可能感兴趣的:(2018-01-31 转载知乎： 如何直观理解矩阵和线性代数？)

2018-01-31 转载知乎：如何直观理解矩阵和线性代数？

你可能感兴趣的:(2018-01-31 转载知乎：如何直观理解矩阵和线性代数？)