_Isaunoya

树链剖分(从入门到入土。)

前置知识：线段树，链式前向星，LCA，DFS序

好了就当你都会了。不会也没关系。

树链剖分通常的操作:
1.x -> y 的路径上修改 2.x -> y 的路径上查询 3. 对于 x 的子树修改 4.对于 x 的子树查询。

一般还有换根操作。树剖也也可以做LCA以及差分操作（但是树剖好像就直接修改了不需要差分）。

树链剖分有两个DFS 这两个DFS就是把一棵树变成一个序列。然后就可以用数据结构来维护了。

第一个DFS 用来求 $fa$（祖先节点） $size$（子树大小）$son$（重儿子） $d$（深度）
重儿子指的是$size$较大的儿子节点。
第二个DFS 用来求$top$（这条链上最顶端的点） $id$（编号）以及其他的赋值操作。但是重儿子要先DFS。

const int N = 1e5 + 10 ;
struct node { int v , nxt ; } ;
node e[N << 1] ;
int head[N] , cnt = 0 ;
inline void Add(int u , int v) { e[++ cnt].v = v ; e[cnt].nxt = head[u] ; head[u] = cnt ; }
int size[N] , son[N] , d[N] ;
inline void Dfs1(int u) { size[u] = 1 ;
  for(register int i = head[u] ; i ; i = e[i].nxt) {
    int v = e[i].v ; if(v == fa[u]) continue ; // 防止无限递归。
    d[v] = d[u] + 1 , fa[v] = u ,  // 记录深度 以及父亲节点
Dfs1(v) ; size[u] += size[v] ; //算出子树大小
    if(size[v] > size[son[u]]) son[u] = v ; //得出u 的 重儿子是 son[u]
  }
}
int top[N] , id[N] , tot = 0 ;
inline void Dfs2(int u , int tp) { top[u] = tp , id[u] = ++ tot ;
  if(! son[u]) return ; Dfs2(son[u] , tp) ;
  for(register int i = head[u] ; i ; i = e[i].nxt) { int v = e[i].v ;
    if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
  }
}

这段代码求的就是下图的结果。

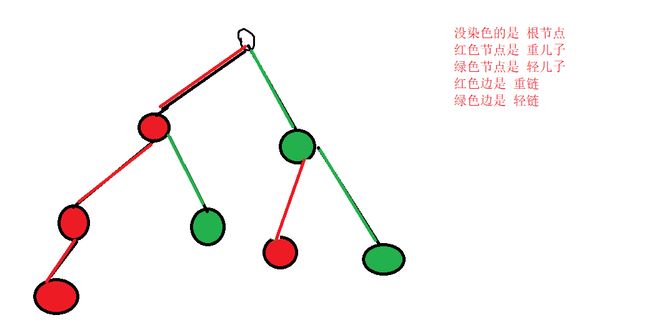
对于这张图 $top$ 指的是重链上最靠上的位置。即链的最高处。
$Question:$ 如果对于最右下的那个节点 top 是自己那么不就死循环了吗？
请读者仔细思考这个问题。

假装你会线段树了。
那么我们想怎么做树上的修改呢？
$id$ 把这个树变成一个序列。
没错就是跳链对于每条重链你可以一下到顶端那么你直接修改这条重链上的值就可以了（数据结构维护）
万一一次重链跳不到那里怎么办？
那么说明了这个点并不是重儿子我们想办法让它跳上去。
反复循环。 DFS1中记录了父亲节点你将它变成它重链上的最高处的父亲节点。
因为这条重链修改过了所以不用管重复。一直反复跳它会跳到链的 LCA 处这也是为什么可以求LCA的原因
对于上面留下的问题…也是一个关于复杂度的证明
假设最坏情况你的修改/查询的点没有一条边在重链上你每次都要往上 fa 一次
但是这种情况出现在满多叉树上这样的话就是最坏的复杂度即 $logn$
那么一般还要套一个线段树所以最坏的复杂度是 $n log^2 n$

写在最后：如果没有规定根的话建议根随机呢万一弄个满二叉树卡你你随机一下就可以避免被卡。
rand()%n+1
善意提醒:建议您下面的代码不要复制粘贴呢自己一遍遍手打。。

【模板】树链剖分

#include 
using namespace std ;
inline int read() { register int res = 0 ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res ;
}
int n , m , r , p ;
const int N = 1000000 + 5 ;
struct E{ int v ;int nxt ; } ;
E edge[N << 1] ;
int a[N] ; int fa[N] ; int w[N] ; int id[N] ; int son[N] ;
int cnt = 0 ; int head[N] ; int Add[N << 2] , laz[N << 2] ;
int dep[N] , siz[N] , t[N] ;
inline void Add_Edge(register int u , register int v) { edge[++ cnt].v = v ; edge[cnt].nxt = head[u] ; head[u] = cnt ; return ; }//建边。
#define l(x) x << 1
#define r(x) x << 1 | 1
inline void Push_down(register int x , register int len) {
    laz[l(x)] += laz[x] ; laz[r(x)] += laz[x] ;
    Add[l(x)] += laz[x] * (len - (len >> 1)) ; Add[r(x)] += laz[x] * (len >> 1) ;
    Add[l(x)] %= p ; Add[r(x)] %= p ;
    laz[x] = 0 ; return ;
}
inline void Build(register int l , register int r , register int rt) {//建树
    if(l == r) { Add[rt] = a[l] ;  return ; }
    register int mid = l + r >> 1 ;
    Build(l , mid , l(rt)) ; Build(mid + 1 , r , r(rt)) ;
    Add[rt] = (Add[l(rt)] + Add[r(rt)]) % p ;
}
inline void Update(register int a , register int b , register int l  , register int r , register int rt , register int k) {//正常的线段树操作
    if(a <= l and r <= b) { laz[rt] += k ; Add[rt] += k * (r - l + 1) ; }
    else {
        if(laz[rt]) Push_down(rt , r - l + 1) ;
        register int mid = l + r >> 1 ;
        if(a <= mid) Update(a , b , l , mid , l(rt) , k) ;
        if(b > mid) Update(a , b , mid + 1 , r , r(rt) , k) ;
        Add[rt] = (Add[l(rt)] + Add[r(rt)]) % p ;
    }
}
int res = 0 ;
inline void query(register int a , register int b , register int  l , register int r , register int rt) {
    if(a <= l and r <= b) { res = (res + Add[rt]) % p ; return ; }
    else {
        if(laz[rt]) Push_down(rt , r - l + 1) ;
        register int mid = l + r >> 1 ;
        if(a <= mid) query(a , b , l , mid , l(rt)) ;
        if(b > mid) query(a , b , mid + 1 , r , r(rt)) ;
    }
}
inline int Query(register int a , register int b , register int l , register int r , register int rt) {//正常的线段树操作
    res = 0 ; query(a , b , l , r , rt) ;
    return res % p ;
}
inline void Upd_Range(register int x , register int y , register int k) {//链上修改
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
         Update(id[t[x]] , id[x] , 1 , n , 1 , k) ;
         x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    Update(id[x] , id[y] , 1 , n , 1 , k) ;
}
inline int Query_Range(register int x , register int y) {//链上查询
    int ans = 0 ;
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
        ans += Query(id[t[x]] , id[x] , 1 , n , 1) ;
        x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    ans += Query(id[x] , id[y] , 1 , n , 1) ;
    return ans % p ;
}
inline int Qson(register int x) { return Query(id[x] , id[x] + siz[x] - 1 , 1 , n , 1) ; } // 子树查询。
inline void Updson(register int x , register int k) { Update(id[x] , id[x] + siz[x] - 1 , 1 , n , 1 , k) ; return ; }
inline void Dfs1(register int x , register int f , register int deep) {
    dep[x] = deep ; fa[x] = f ; siz[x] = 1 ;
    int max_son = -1 ;
    for(register int i = head[x] ; i ; i = edge[i].nxt) {
        register int v = edge[i].v ;
        if(v == f) continue ;
        Dfs1(v , x , deep + 1) ;siz[x] += siz[v] ;
        if(siz[v] > max_son) max_son = siz[v] , son[x] = v ;
    }
}
int tot = 0 ;
inline void Dfs2(register int x , register int tf) {
    id[x] = ++ tot ; a[tot] = w[x] ; t[x] = tf ; // a 数组重新赋值
    if(! son[x]) return ;
    Dfs2(son[x] , tf) ;
    for(register int i = head[x] ; i ; i = edge[i].nxt) {
        int v = edge[i].v ;
        if(v == fa[x] or v == son[x]) continue ;
        Dfs2(v , v) ;
    }
}
signed main() {
    n = read() ; m = read() ; r = read() ; p = read() ;
    for(register int i = 1 ; i <= n ; i ++) w[i] = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() ;
        Add_Edge(u , v) ;
        Add_Edge(v , u) ;
    }
    Dfs1(r , 0 , 1) ; Dfs2(r , r) ; Build(1 , n , 1) ;
    for( ; m -- ; ) {
        register int opt = read() ;
        if(opt == 1) {
            register int x = read() , y = read() , k = read() ;
            Upd_Range(x , y , k % p) ;
        }
        if(opt == 2) {
            register int x = read() , y = read() ;
            printf("%d\n" , Query_Range(x , y)) ;
        }
        if(opt == 3) {
            register int x = read() , y = read() ;
            Updson(x , y) ;
        }
        if(opt == 4) { printf("%d\n" , Qson(read())) ; }
    }
    return 0 ;
}

[USACO11DEC]牧草种植Grass Planting

链上修改单点查询。
对于这个题目要修改的是边的权值。
这里有一个技巧是把边的权值下传给点然后把最上面的点忽略掉。（易证这样是可以的。）
然后进行基本的操作就可以了。

#include
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
    register int x = 0 , f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
    return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
    return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
    return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
    int ans = 1 ;
    for( ; y ; y >>= 1 , x = (x * x) % Mod)
        if(y & 1) ans = (ans * x) % Mod ;
    return ans ;
}
int n , m ;
struct node {
  int v , nxt ;
} ;
const int N = 1e5 + 10 ;
node e[N << 1] ;
int head[N] , cnt = 0 ;
inline void Add(int u , int v) {
  e[++ cnt].v = v ;
  e[cnt].nxt = head[u] ;
  head[u] = cnt ;
  return ;
}
int fa[N] ;
int top[N] ;
int d[N] ;
int size[N] ;
int son[N] ;
int id[N] , idx = 0 ;
int a[N] ;
int sum[N << 2] ;
inline void build(int l , int r , int rt) {
  if(l == r) {
    sum[rt] = a[l] ;
    return ;
  }
  int mid = l + r >> 1 ;
  build(l , mid , rt << 1) ;
  build(mid + 1 , r , rt << 1 | 1) ;
}
int tag[N << 2] ;
inline void Push_down(int rt , int l , int r) {
  if(! tag[rt]) return ;
  tag[rt << 1] += tag[rt] ;
  tag[rt << 1 | 1] += tag[rt] ;
  int mid = l + r >> 1 ;
  sum[rt << 1] += tag[rt] * (mid - l + 1) ;
  sum[rt << 1 | 1] += tag[rt] * (r - mid) ;
  tag[rt] = 0 ;
  return ;
}
inline void Update(int a , int b , int l , int r , int rt) {
  if(a <= l && r <= b) { sum[rt] += (r - l + 1) ; tag[rt] ++ ; return ; }
  Push_down(rt , l , r) ;
  int mid = l + r >> 1 ;
  if(a <= mid) Update(a , b , l , mid , rt << 1) ;
  if(b > mid) Update(a , b , mid + 1 , r , rt << 1 | 1) ;
  sum[rt] = sum[rt << 1] + sum[rt << 1 | 1] ;
}
inline int Query(int a , int b , int l , int r , int rt) {
  if(a <= l && r <= b) return sum[rt] ;
  Push_down(rt , l , r) ;
  int mid = l + r >> 1 , ans = 0 ;
  if(a <= mid) ans += Query(a , b , l , mid , rt << 1) ;
  if(b > mid) ans += Query(a , b , mid + 1 , r , rt << 1 | 1) ;
  return ans ;
}
inline void Dfs(int u) {
  size[u] = 1 ;
  for(register int i = head[u] ; i ; i = e[i].nxt) {
    int v = e[i].v ;
    if(v == fa[u]) continue ;
    fa[v] = u ;
    d[v] = d[u] + 1 ;
    Dfs(v) ;
    size[u] += size[v] ;
    if(size[son[u]] < size[v]) son[u] = v ;
  }
}
inline void Dfs2(int u , int t) {
  top[u] = t ;
  a[idx] = 0 ;
  id[u] = ++ idx ;
  if(! son[u]) return ;
  Dfs2(son[u] , t) ;
  for(register int i = head[u] ; i ; i = e[i].nxt) {
    int v = e[i].v ;
    if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
  }
}
inline void Change(int x , int y) {
  int fx = top[x] ;
  int fy = top[y] ;
  while(fx ^ fy) {
    if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
    Update(id[fx] , id[x] , 1 , n , 1) ;
    x = fa[fx] ;
    fx = top[x] ;
  }
  if(d[x] > d[y]) swap(x , y) ;
  Update(id[x] + 1 , id[y] , 1 , n , 1) ;
}
inline int Query_Range(int x , int y) {
  int ans = 0 ;
  int fx = top[x] ;
  int fy = top[y] ;
  while(fx ^ fy) {
    if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
    ans += Query(id[fx] , id[x] , 1 , n , 1) ;
    x = fa[fx] ;
    fx = top[x] ;
  }
  if(d[x] > d[y]) swap(x , y) ;
  ans += Query(id[x] + 1 , id[y] , 1 , n , 1) ;
  return ans ;
}
signed main() {
  n = read() ; m = read() ;
  for(register int i = 1 ; i <= n - 1 ; i ++) {
    int u = read() , v = read() ;
    Add(u , v) ;
    Add(v , u) ;
  }
  Dfs(1) ;
  Dfs2(1 , 0) ;
  build(1 , n , 1) ;
  for(register int i = 1 ; i <= m ; i ++) {
    register char c = getchar() ;
    while(c != 'P' && c != 'Q') c = getchar() ;
    int u = read() , v = read() ;
    if(c == 'P') Change(u , v) ;
    else printf("%lld\n" , Query_Range(u , v)) ;
  }
    return 0 ;
}

Qtree1

同样的边权化成点权然后单点修改

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge
int n ;

//============================================SegTree
struct SegTree {
    int val ;
    int max ;
};
const int N = 2e5 + 10 ;
SegTree t[N << 2] ;
int a[N] ;
inline void build(int l , int r , int rt) {
    if( l == r ) {
        t[rt].max = t[rt].val = a[l] ;
        return ;
    }
    int mid = l + r >> 1 ;
    build(l , mid , rt << 1) ;
    build(mid + 1 , r , rt << 1 | 1) ;
    t[rt].max = max(t[rt << 1].max , t[rt << 1 | 1].max) ;
}
inline void Change(int x , int l , int r , int rt , int val) {
    if(l == r) {
        t[rt].max = t[rt].val = val ;
        return ;
    }
    int mid = l + r >> 1 ;
    if(x <= mid) Change(x , l , mid , rt << 1 , val) ;
    else Change(x , mid + 1 , r , rt << 1 | 1 ,val ) ;
    t[rt].max = max(t[rt << 1].max , t[rt << 1 | 1].max) ;
}
inline int Query_Max(int a , int b , int  l, int r , int rt) {
    if(a > b) return 0 ;
    if(a <= l && r <= b) return t[rt].max ;
    int ans = 0 ;
    int mid = l + r >> 1 ;
    if(a <= mid) ans = max(ans , Query_Max(a , b , l , mid , rt << 1)) ;
    if(b > mid) ans = max(ans , Query_Max(a , b , mid + 1 , r , rt << 1 | 1)) ;
    return ans ;
}
//========================================================================

struct node {
    int v ;
    int nxt ;
    int w ;
};
node e[N << 1] ;
int head[N] ;
int cnt = 0 ;
inline void Add_Edge(int u , int v , int w) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ;
    e[cnt].w  = w ;
    head[u] = cnt ;
    return ;
}
int size[N] ;
int son[N] ;
int d[N] ;
int fst[N] ;
int id[N] ;
int top[N] ;
int fa[N] ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        d[v] = d[u] + 1 ;
        fst[v] = e[i].w ;
        fa[v] = u ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
}
int idx = 0 ;
inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    a[idx] = fst[u] ;
    top[u] = t ; 
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) {
            Dfs2(v , v) ;
        }
    }
}
inline int Query_Range(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    int ans = 0 ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        ans = max(ans , Query_Max(id[fx] , id[x] , 1 , n , 1)) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    ans = max(ans , Query_Max(id[x] + 1 , id[y] , 1 , n , 1)) ;
    return ans ;
}
inline int getopt() {
    string s ;
    register char c = getchar() ;
    while(isspace(c)) c = getchar() ;
    while(! isspace(c)) {
        s += c ;
        c = getchar() ;
    }
    if(s == "DONE") return -1 ;
    if(s == "QUERY") return 0 ;
    return 1 ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    for(register int i = 1 ; i < n ; i ++) {
        int u = read() , v = read() , w = read() ;
        Add_Edge(u , v , w) ;
        Add_Edge(v , u , w) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    build(1 , n , 1) ;
    while(1) {
        int opt = getopt() ;
        if(opt == -1) {
            return 0 ;
        }
        if(opt == 0) {
            int x = read() , y = read() ;
            if(x == y) {
                puts("0") ;
                continue ;
            }
            else {
                write(Query_Range(x , y)) ;
            }
        }
        else {
            int x = read() , y = read() ;
            int u = e[x * 2 - 1].v ;
            int v = e[x * 2].v ;
            if(u == fa[v]) swap(u , v) ;
            Change(id[u] , 1 , n , 1 , y) ;
        }
    }
    return 0 ;
} // 这份代码会T掉一个点…

[USACO15DEC]最大流Max Flow

树剖是可以求LCA的以这题为例。
这题是需要把压力给两个点两个点加上1 然后这两个点的$LCA$减掉1 因为这个点也需要加上1 所以我们只能把这个1在$fa_LCA$减掉
这样递归到最底下然后一直往上加显然就是这棵树的权值

#include
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
    register int x = 0 , f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
    return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
    return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
    return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
    int ans = 1 ;
    for( ; y ; y >>= 1 , x = (x * x) % Mod)
        if(y & 1) ans = (ans * x) % Mod ;
    return ans ;
}
int n ;
struct node {
  int v , nxt ;
} ;
const int N = 50000 + 5 ;
node e[N << 1] ;
int head[N] , cnt = 0 ;
inline void Add(int u , int v) {
  e[++ cnt].v = v ;
  e[cnt].nxt = head[u] ;
  head[u] = cnt ;
  return ;
}
int fa[N] ;
int size[N] ;
int son[N] ;
int top[N] ;
int d[N] ;
inline void Dfs(int u) {
  size[u] = 1 ;
  for(register int i = head[u] ; i ; i = e[i].nxt) {
    int v = e[i].v ;
    if(v == fa[u]) continue ;
    fa[v] = u ;
    d[v] = d[u] + 1 ;
    Dfs(v) ;
    size[u] += size[v];
    if(size[v] > size[son[u]]) son[u] = v ;
  }
}
inline void Dfs2(int u , int t) {
  top[u] = t ;
  if(! son[u]) return ;
  Dfs2(son[u] , t) ;
  for(register int i = head[u] ; i ; i = e[i].nxt) {
    int v = e[i].v ;
    if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
  }
}
inline int Lca(int x , int y) {//树剖求LCA
  int fx = top[x] , fy = top[y] ;
  while(fx ^ fy) {
    if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
    x = fa[fx] ;
    fx = top[x] ;
  }
  if(d[x] > d[y]) swap(x , y) ;
  return x ;
}
int ad[N] ;
int ans = 0 ;
inline void Getans(int u , int father) { // 不断往下找 然后更新答案
  for(register int i = head[u] ; i ; i = e[i].nxt) {
    int v = e[i].v ;
    if(v == father) continue ;
    Getans(v , u) ;
    ad[u] += ad[v] ;
  }
  ans = max(ans , ad[u]) ;
}
signed main() {
  n = read() ; int k = read() ;
  for(register int i = 1 ; i <= n - 1 ;  i ++) {
    int u = read() , v = read() ;
    Add(u , v) ;
    Add(v , u) ;
  }
  Dfs(1) ;
  Dfs2(1 , 0) ;
  for(register int i = 1 ; i <= k ; i ++) {
    int u = read() , v = read() ;
    int lca = Lca(u , v) ;
    ad[u] ++ ;
    ad[v] ++ ;
    ad[lca] -- ;
    ad[fa[lca]] -- ;
  }// 树上差分
  Getans(1 , 0) ;
  printf("%lld" , ans) ;
    return 0 ;
}

[HEOI2016/TJOI2016]树

技巧题
这题是可以在链上二分的但是主流做法好像不是这个？
链上二分要注意是反过来的。。

#include
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
    register int x = 0 , f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
    return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
    return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
    return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
    int ans = 1 ;
    for( ; y ; y >>= 1 , x = (x * x) % Mod)
        if(y & 1) ans = (ans * x) % Mod ;
    return ans ;
}
int n , m ;
struct node {
    int v , nxt ;
} ;
const int N = 1e5 + 10 ;
node e[N << 1] ;
int head[N] , cnt = 0 ;
inline void Add(int u , int v) { e[++ cnt].v = v , e[cnt].nxt = head[u] , head[u] = cnt ; }
int fa[N] , size[N] , son[N] , d[N] ;
inline void Dfs(int u) { size[u] = 1 ; for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ; if(v == fa[u]) continue ;
        d[v] = d[u] + 1 , fa[v] = u , Dfs(v) , size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
}
int top[N] , id[N] , idx = 0 , f[N] ;
inline void Dfs2(int u , int t) { id[u] = ++ idx , top[u] = t , f[idx] = u ;
    if(! son[u]) return ; Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ; if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
    }
}
int sum[N << 2] ;
inline void build(int l , int r , int rt){
    if(l == r) { sum[rt] = 0 ; return ; }
    int mid = l + r >> 1 ; build(l , mid , rt << 1) , build(mid + 1 , r , rt << 1 | 1) ;
}
inline void upd(int x , int l , int r , int rt) {
    if(l == r) { sum[rt] = 1 ; return ; }
    int mid = l + r >> 1 ;
    if(x <= mid) upd(x , l , mid , rt << 1) ; else upd(x , mid + 1 , r , rt << 1 | 1) ;
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1] ;
}
inline int query(int a , int b , int l , int r , int rt) {
    if(a <= l && r <= b) { return sum[rt] ; }
    int mid = l + r >> 1 , ans = 0 ;
    if(a <= mid) ans += query(a , b , l , mid , rt << 1) ;
    if(b > mid) ans += query(a , b ,  mid + 1 , r , rt << 1 | 1) ;
    return ans ;
}
inline int chk(int l , int r) { // 二分找答案
    if(l == r) return l ;
    int mid = l + r >> 1 ;
    if(query(mid + 1 , r , 1 , n , 1)) return chk(mid + 1 , r) ; // 反过来。
    else return chk(l , mid) ;
}
inline int Find(int x , int y = 1) { // 求答案 因为最近的点一定是在 1 ~ x 的这条路径上。
    int fx = top[x] , fy = top[y] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        int q = query(id[fx] , id[x] , 1 , n , 1) ;
        if(q) return chk(id[fx] , id[x]) ;
        else { x = fa[fx] , fx = top[x] ; continue ; }
    }
    if(d[x] > d[y]) swap(x , y) ;
    return chk(id[x] , id[y]) ;
}
signed main() {
    n = read() ; m = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) { int u = read() , v = read() ; Add(u , v) , Add(v , u) ;}
    Dfs(1) , Dfs2(1 , 0) , build(1 , n , 1) ;
    for(register int i = 1 ; i <= m ; i ++) {
        register char c = getchar() ;
        while(c != 'C' && c != 'Q') c = getchar() ;
        int x = read() ;
        if(c == 'C') upd(id[x] , 1 , n , 1) ;
        if(c == 'Q') printf("%lld\n" , f[Find(x)]) ;
    }
    return 0 ;
}

[国家集训队]旅游
sol

//Isaunoya
#include
using namespace std ;
inline int read() {
    register int x = 0 ;
    register int f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
int st[105] ;
template < typename T > inline void write(T x , char c = '\n') {
    int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge
//#define int long long
#define swap(x , y) x ^= y ^= x ^= y
int n ;
const static int N = 200000 + 5 ;
int a[N] ;
namespace SegTree {
    struct Node {
        int mn ; // the min
        int mx ; // the max
        int add ; // the sum
        int lazy ; // the sign
    };
    Node t[N << 2] ;
    inline void Push_down(int rt) {
        if(t[rt].lazy) {
            t[rt << 1].add = - t[rt << 1].add ;
            t[rt << 1 | 1].add = - t[rt << 1 | 1].add ;
            t[rt << 1].lazy ^= 1 ;
            t[rt << 1 | 1].lazy ^= 1 ;
            swap(t[rt << 1].mx , t[rt << 1].mn) ;
            swap(t[rt << 1 | 1].mx , t[rt << 1 | 1].mn) ;
            t[rt << 1].mx = - t[rt << 1].mx ;
            t[rt << 1].mn = - t[rt << 1].mn ;
            t[rt << 1 | 1].mx = - t[rt << 1 | 1].mx ;
            t[rt << 1 | 1].mn = - t[rt << 1 | 1].mn ;
            t[rt].lazy = 0 ;
        }
        return ;
    }
    //==============================================push_down
    inline void Push_Up(int rt) {
        t[rt].add = t[rt << 1].add + t[rt << 1 | 1].add ;
        t[rt].mx = max(t[rt << 1].mx , t[rt << 1 | 1].mx) ;
        t[rt].mn = min(t[rt << 1].mn , t[rt << 1 | 1].mn) ;
        return ;
    }
    //==============================================push_up
    inline void build(int l , int r , int rt) {
        if(l == r) {
            t[rt].add = t[rt].mn = t[rt].mx = a[l] ;
            return ;
        }
        int mid = l + r >> 1 ;
        build(l , mid , rt << 1) ;
        build(mid + 1 , r , rt << 1 | 1) ;
        Push_Up(rt) ;
    }
    //==============================================build
    inline void Add(int x , int l , int r , int rt , int val) {
        if(l == r) {
            t[rt].add = t[rt].mn = t[rt].mx = val ;
            return ;
        }
        int mid = l + r >> 1 ;
        Push_down(rt) ;
        if(x <= mid) Add(x , l , mid , rt << 1 , val) ;
        else Add(x , mid + 1 , r , rt << 1 | 1 , val) ;
        Push_Up(rt) ;
    }
    //==============================================change x - > val
    inline void Change(int a , int b , int l , int r , int rt) {
        if(a > r || b < l) return ;
        if(a <= l && r <= b) {
            t[rt].add = - t[rt].add ;
            t[rt].lazy ^= 1 ;
            swap(t[rt].mx , t[rt].mn) ;
            t[rt].mx = - t[rt].mx ;
            t[rt].mn = - t[rt].mn ;
            return ;
        }
        int mid = l + r >> 1 ;
        Push_down(rt) ;
        Change(a , b , l , mid , rt << 1) ;
        Change(a , b , mid + 1 , r , rt << 1 | 1) ;
        Push_Up(rt) ;
    }
    //===============================================change x - > -x
    inline int Sum(int a , int b , int l , int r , int rt) {
        if(a > r || b < l) return 0 ;
        if(a <= l && r <= b) return t[rt].add ;
        int mid = l + r >> 1 ;
        Push_down(rt) ;
        int ans = 0 ;
        ans += Sum(a , b , l , mid , rt << 1 ) ;
        ans += Sum(a , b , mid + 1 , r , rt << 1 | 1) ;
        Push_Up(rt) ;
        return ans ;
    }
    //====================================================== a - > b sum
    inline int Min(int L , int R , int l , int r , int rt) {
        if(L > r || R < l) return INT_MAX ;
        if(L <= l && r <= R) return t[rt].mn ;
        int ans = INT_MAX ;
        int mid = l + r >> 1 ;
        Push_down(rt) ;
        if(L <= mid) ans = min(ans , Min(L , R , l , mid , rt << 1)) ;
        if(R > mid) ans = min(ans , Min(L , R, mid + 1 , r , rt << 1 | 1)) ;
        Push_Up(rt) ;
        return ans ;
    }
    //====================================================== a - > b min
    inline int Max(int L , int R , int l , int r , int rt) {
        if(L > r || R < l) return INT_MIN ;
        if(L <= l && r <= R) return t[rt].mx ;
        int ans = INT_MIN ;
        int mid = l + r >> 1 ;
        Push_down(rt) ;
        if(L <= mid) ans = max(ans , Max(L , R , l , mid , rt << 1)) ;
        if(R > mid) ans = max(ans , Max(L , R, mid + 1 , r , rt << 1 | 1)) ;
        Push_Up(rt) ;
        return ans ;
    }
    //====================================================== a - > b max
}
//===========================================================SegTree
namespace SLPF {
    struct node {
        int v ;
        int nxt ;
        int w ;
    };
    int fa[N] ; int id[N] ; int son[N] ;
    int size[N] ; int d[N] ; int top[N] ;
    int fst[N] ;
    node e[N << 1] ;
    int tot = 0 ;
    int head[N] ; int cnt = 0 ;
    inline void Add_Edge(int u , int v , int w) {
        e[++ cnt].v = v ;
        e[cnt].nxt = head[u] ;
        e[cnt].w = w ;
        head[u] = cnt ;
        return ;
    }
    inline void Dfs1(int u) {
        size[u] = 1 ;
        for(register int i = head[u] ; i ; i = e[i].nxt) {
            int v = e[i].v ;
            if(v ^ fa[u]) {
                d[v] = d[u] + 1 ;
                fa[v] = u ;
                fst[v] = e[i].w ;
                Dfs1(v) ;
                size[u] += size[v] ;
                if(size[v] > size[son[u]]) son[u] = v ;
            }
        }
    }
    inline void Dfs2(int u , int t) {
        id[u] = ++ tot ;
        top[u] = t ;
        a[tot] = fst[u] ;
        if(son[u]) Dfs2(son[u] , t) ;
        for(register int i = head[u] ; i ; i = e[i].nxt) {
            int v = e[i].v ;
            if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
        }
    }
    //========================================================Dfs1 && Dfs2

    inline void Change_Range(int x , int y) {
        int fx = top[x] ;
        int fy = top[y] ;
        while(fx ^ fy) {
            if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
            SegTree::Change(id[fx] , id[x] , 1 , tot , 1) ;
            x = fa[fx] ;
            fx = top[x] ;
        }
        if(id[x] > id[y]) swap(x , y) ;
        SegTree::Change(id[x] + 1 , id[y] , 1 , tot , 1) ;
    }
    inline int Query_Sum(int x , int y) {
        int fx = top[x] ;
        int fy = top[y] ;
        int ans = 0 ;
        while(fx ^ fy) {
            if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
            ans += SegTree::Sum(id[fx] , id[x] , 1 , tot , 1) ;
            x = fa[fx] ;
            fx = top[x] ;
        }
        if(id[x] > id[y]) swap(x , y) ;
        ans += SegTree::Sum(id[x] + 1 , id[y] , 1 , tot , 1) ;
        return ans ;
    }
    inline int Query_Min(int x , int y) {
        int fx = top[x] ;
        int fy = top[y] ;
        int ans = INT_MAX ;
        while(fx ^ fy) {
            if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
            ans = min(ans , SegTree::Min(id[fx] , id[x] , 1 , tot , 1)) ;
            x = fa[fx] ;
            fx = top[x] ;
        }
        if(id[x] > id[y]) swap(x , y) ;
        ans = min(ans , SegTree::Min(id[x] + 1 , id[y] , 1 , tot , 1)) ;
        return ans ;
    }
    inline int Query_Max(int x , int y) {
        int fx = top[x] ;
        int fy = top[y] ;
        int ans = INT_MIN ;
        while(fx ^ fy) {
            if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
            ans = max(ans , SegTree::Max(id[fx] , id[x] , 1 , tot , 1)) ;
            x = fa[fx] ;
            fx = top[x] ;
        }
        if(id[x] > id[y]) swap(x , y) ;
        ans = max(ans , SegTree::Max(id[x] + 1 , id[y] , 1 , tot , 1)) ;
        return ans ;
    }
}
using namespace SLPF ;
inline int getopt() {
    string s = "" ;
    register char c = getchar() ;
    while(isspace(c)) c = getchar() ;
    while(! isspace(c)) {
        s += c ;
        c = getchar() ;
    }
    if(s == "C") return 0 ;
    if(s == "N") return 1 ;
    if(s == "SUM") return 2 ;
    if(s == "MAX") return 3 ;
    if(s == "MIN") return 4 ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() , w = read() ;
        u ++ , v ++ ;
        Add_Edge(u , v , w) ;
        Add_Edge(v , u , w) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 0) ;
    SegTree::build(1 , n , 1) ;
    for(register int t = read() ; t -- ; ) {
        int opt = getopt() ;
//      write(opt) ;
        if(opt == 0) {
            int x = read() , y = read() ;
            x ++ ;
            SegTree::Add(id[x] , 1 , n , 1 , y) ;
        }
        if(opt == 1) {
            int x = read() , y = read() ;
            x ++ , y ++ ;
            Change_Range(x , y) ;
        }
        if(opt == 2) {
            int x = read() , y = read() ;
            x ++ , y ++ ;
            write(Query_Sum(x , y)) ;
        }
        if(opt == 3) {
            int x = read() , y = read() ;
            x ++ , y ++ ;
            write(Query_Max(x , y)) ;
        }
        if(opt == 4) {
            int x = read() , y = read() ;
            x ++ , y  ++ ;
            write(Query_Min(x , y)) ;
        }
    }
    return 0 ;
}

[ZJOI2008]树的统计

与模板题差不多。。

//Isaunoya
#include 
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
int n , m , r , p ;
const int N = 10000000 + 5 ;
struct E{ int v ;int nxt ; } ;
E edge[N << 1] ;
int a[N] ; int fa[N] ; int w[N] ; int id[N] ; int son[N] ;
int cnt = 0 ; int head[N] ; int Add[N << 2] , laz[N << 2] ;
int mx[N << 2] ;
int dep[N] , siz[N] , t[N] ;
inline void Add_Edge(register int u , register int v) { edge[++ cnt].v = v ; edge[cnt].nxt = head[u] ; head[u] = cnt ; return ; }
#define l(x) x << 1
#define r(x) x << 1 | 1
inline void Push_down(register int x , register int len) {
    laz[l(x)] += laz[x] ; laz[r(x)] += laz[x] ;
    Add[l(x)] += laz[x] * (len - (len >> 1)) ; Add[r(x)] += laz[x] * (len >> 1) ;
    Add[l(x)] %= p ; Add[r(x)] %= p ;
    laz[x] = 0 ; return ;
}
inline void Build(register int l , register int r , register int rt) {
    if(l == r) { mx[rt] = Add[rt] = a[l] ;  return ; }
    register int mid = l + r >> 1 ;
    Build(l , mid , l(rt)) ; Build(mid + 1 , r , r(rt)) ;
    Add[rt] = (Add[l(rt)] + Add[r(rt)])  ;
    mx[rt] = max(mx[rt << 1] , mx[rt << 1 | 1]) ;
}
inline void Update(register int a , register int b , register int l  , register int r , register int rt , register int k) {
    if(a <= l and r <= b) { laz[rt] += k ; Add[rt] += k * (r - l + 1) ; }
    else {
        if(laz[rt]) Push_down(rt , r - l + 1) ;
        register int mid = l + r >> 1 ;
        if(a <= mid) Update(a , b , l , mid , l(rt) , k) ;
        if(b > mid) Update(a , b , mid + 1 , r , r(rt) , k) ;
        Add[rt] = (Add[l(rt)] + Add[r(rt)])  ;
        mx[rt] = max(mx[rt << 1] , mx[rt << 1 | 1]) ;
    }
}
inline void upd(int x , int l , int r , int rt , int v) {
    if(l == r) {
        mx[rt] = Add[rt] = v ;
        return ;
    }
    int mid = l + r >> 1 ;
    if(x <= mid) upd(x , l , mid , rt << 1 , v) ;
    else upd(x , mid + 1 , r , rt << 1 | 1 , v) ;
    Add[rt] = (Add[l(rt)] + Add[r(rt)])  ;
    mx[rt] = max(mx[rt << 1] , mx[rt << 1 | 1]) ;
}
int res = 0 ;
inline void query(register int a , register int b , register int  l , register int r , register int rt) {
    if(a <= l and r <= b) { res = (res + Add[rt])  ; return ; }
    else {
        if(laz[rt]) Push_down(rt , r - l + 1) ;
        register int mid = l + r >> 1 ;
        if(a <= mid) query(a , b , l , mid , l(rt)) ;
        if(b > mid) query(a , b , mid + 1 , r , r(rt)) ;
    }
}
inline int Query(register int a , register int b , register int l , register int r , register int rt) {
    res = 0 ; query(a , b , l , r , rt) ;
    return res  ;
}
inline int Query_Max(int a , int b , int l , int r , int rt) {
    if(a <= l && r <= b) return mx[rt] ;
    int mid = l + r >> 1 ;
    int ans = INT_MIN ;
    if(a <= mid) ans = max(ans , Query_Max(a , b , l , mid , rt << 1)) ;
    if(b > mid) ans = max(ans , Query_Max(a , b , mid + 1 , r , rt << 1 | 1)) ;
    return ans ;
}
inline void Upd_Range(register int x , register int y , register int k) {
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
         Update(id[t[x]] , id[x] , 1 , n , 1 , k) ;
         x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    Update(id[x] , id[y] , 1 , n , 1 , k) ;
}
inline int Query_Range(register int x , register int y) {
    int ans = 0 ;
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
        ans += Query(id[t[x]] , id[x] , 1 , n , 1) ;
        x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    ans += Query(id[x] , id[y] , 1 , n , 1) ;
    return ans  ;
}
inline int Query_Max_Range(register int x , register int y) {
    int ans = INT_MIN ;
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
        ans = max(ans , Query_Max(id[t[x]] , id[x] , 1 , n , 1)) ;
        x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    ans = max(ans , Query_Max(id[x] , id[y] , 1 , n , 1)) ;
    return ans  ;
}
inline int Qson(register int x) { return Query(id[x] , id[x] + siz[x] - 1 , 1 , n , 1) ; }
inline void Updson(register int x , register int k) { Update(id[x] , id[x] + siz[x] - 1 , 1 , n , 1 , k) ; return ; }
inline void Dfs1(register int x , register int f , register int deep) {
    dep[x] = deep ; fa[x] = f ; siz[x] = 1 ;
    int max_son = -1 ;
    for(register int i = head[x] ; i ; i = edge[i].nxt) {
        register int v = edge[i].v ;
        if(v == f) continue ;
        Dfs1(v , x , deep + 1) ;siz[x] += siz[v] ;
        if(siz[v] > max_son) max_son = siz[v] , son[x] = v ;
    }
}
int tot = 0 ;
inline void Dfs2(register int x , register int tf) {
    id[x] = ++ tot ; a[tot] = w[x] ; t[x] = tf ;
    if(! son[x]) return ;
    Dfs2(son[x] , tf) ;
    for(register int i = head[x] ; i ; i = edge[i].nxt) {
        int v = edge[i].v ;
        if(v == fa[x] or v == son[x]) continue ;
        Dfs2(v , v) ;
    }
}
inline int getopt() {
    string s = "" ; register char c = getchar() ;
    while(isspace(c)) c = getchar() ;
    while(! isspace(c)) {
        s += c ;
        c = getchar() ;
    }
    if(s == "CHANGE") return 0 ;
    if(s == "QMAX") return 1 ;
    if(s == "QSUM") return 2 ; 
}
signed main() {
    n = read() ; 
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() ;
        Add_Edge(u , v) ;
        Add_Edge(v , u) ;
    }for(register int i = 1 ; i <= n ; i ++) w[i] = read() ;
    m = read() ; r = 1 ;
    Dfs1(r , 0 , 1) ; Dfs2(r , r) ; Build(1 , n , 1) ;
    for( ; m -- ; ) {
        int opt = getopt() ;
//        cout  << opt ;
        int u = read() , v = read() ;
        if(opt == 0) {
            upd(id[u] , 1 , n , 1 , v) ;
        }
        if(opt == 1) {
            write(Query_Max_Range(u , v)) ;
        }
        if(opt == 2) {
            write(Query_Range(u , v)) ;
        }
    }
    return 0 ;
}

[SHOI2012]魔法树

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge

#define int long long
//==============================================================edge
struct node {
    int v ;
    int nxt ;
};
int n ;
const int N = 100000 + 5 ;
node e[N << 1] ;
int cnt = 0 ; int head[N] ;
inline void Add(int u , int v) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ;
    head[u] = cnt ;
    return ;
}
int size[N] ;
int son[N] ; int id[N] ;
int idx = 0 ; int d[N] ;
int top[N] ; int fa[N] ;
//================================================================slpf
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        fa[v] = u ;
        d[v] = d[u] + 1 ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
}

inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    top[u] = t ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
    }
}
//=======================================================Segment_Tree
struct Seg {
    int sum ;
    int tag ;
};
Seg t[N << 2] ;
inline void Push_down(int rt , int l , int r) {
    if(t[rt].tag) {
        t[rt << 1].tag += t[rt].tag ;
        t[rt << 1 | 1].tag += t[rt].tag ;
        int mid = l + r >> 1 ;
        t[rt << 1].sum += (mid - l + 1) * t[rt].tag ;
        t[rt << 1 | 1].sum += (r - mid) * t[rt].tag ;
        t[rt].tag = 0 ;
        return ;
    }
}
inline void Push_up(int rt) {
    t[rt].sum = t[rt << 1].sum + t[rt << 1 | 1].sum ;
}
inline void build(int l , int r , int rt) {
    if(l == r) {
        t[rt].sum = 0 ;
        return ;
    }
    int mid = l + r >> 1 ;
    build(l , mid , rt << 1) ;
    build(mid + 1 , r , rt << 1 | 1) ;
    Push_up(rt) ;
}
inline void Change(int a , int b , int l , int r , int rt , int val) {
    if(a <= l && r <= b) {
        t[rt].sum += (r - l + 1) * val ;
        t[rt].tag += val ;
        return ;
    }
    Push_down(rt , l , r) ;
    int mid = l + r >> 1 ;
    if(a <= mid) Change(a , b , l , mid , rt << 1 , val) ;
    if(b > mid) Change(a , b , mid + 1 , r , rt << 1 | 1 , val) ;   
    Push_up(rt) ;
    return ;
}
inline int Query(int a , int b , int l , int r , int rt) {
    if(a <= l && r <= b) return t[rt].sum ;
    Push_down(rt , l , r) ;
    int mid = l + r >> 1 ;
    int ans = 0 ;
    if(a <= mid) ans += Query(a , b , l , mid , rt << 1) ;
    if(b > mid) ans += Query(a , b , mid + 1 , r , rt << 1 | 1) ;
    return ans ;
}

inline void Change_Range(int x , int y , int val) {
    int fx = top[x] ;
    int fy = top[y] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        Change(id[fx] , id[x] , 1 ,n , 1 , val) ;
        x = fa[fx] ; 
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    Change(id[x] , id[y] , 1 , n , 1 , val) ;
    return ;
}
//inline int Query_Range(int x , int y) {
//  int fx = top[x] ;
//  int fy = top[y] ;
//  int ans = 0 ;
//  while(fx  ^ fy) {
//      if(d[fx] < d[fy]) swap(x ,y) , swap(fx , fy) ;
//      ans += Query(id[fx] , id[x] , 1 , n , 1) ;
//      x = fa[fx] ;
//      fx = top[x] ;
//  }
//  if(id[x] > id[y]) swap(x , y) ;
//  ans += Query(id[x] , id[y] , 1 , n , 1) ;
//  return ans ;
//}
inline int Query_Son(int x) { return Query(id[x] , id[x] + size[x] - 1 , 1 , n , 1) ; }
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v= read() ;
        u ++ ; v ++ ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    build(1 , n , 1) ;
    for(register int q = read() ; q -- ; ) {
        register char c = getchar() ;
        for( ; c != 'Q' && c != 'A' ; c = getchar()) ;
        if(c == 'A') {
            int x = read() , y = read() ;
            x ++ , y ++ ;
            int val = read() ;
            Change_Range(x , y , val) ;
        } 
        if(c == 'Q') {
            int x = read() ;
            x ++ ;
            write(Query_Son(x)) ;
        } 
    }
    return 0 ;
}

APIO[部落冲突]
sol

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge
int n ;
vector < pair < int , int > > v ;
const int N = 3e5 + 10 ;
int a[N] ;
struct node {
    int v ;
    int nxt ;
};
node e[N << 1] ; int head[N] ;
int cnt = 0 ;
inline void Add(int u , int v) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ;
    head[u] = cnt ;
    return ;
} 
int size[N] ;
int top[N] , son[N] ;
int fa[N] ; int id[N] ; int d[N] ;
int idx = 0 ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u]) {
            fa[v] = u ;
            d[v] = d[u] + 1 ;
            Dfs1(v) ;
            size[u] += size[v] ;
            if(size[son[u]] < size[v]) son[u] = v ;
        }
    }
}
inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    top[u] = t ;
    a[idx] = 0 ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) {
            Dfs2(v , v) ;
        }
    }
}
int sum[N << 2] ;
int tag[N << 2] ;
inline void build(int l , int r , int rt) {
    if(l == r) {
        sum[rt] = a[l] ; 
        tag[rt] = 0 ;
        return ;
    }
    int mid = l + r >> 1 ;
    build(l , mid , rt << 1) ;
    build(mid + 1 , r , rt << 1 | 1) ;
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1] ;
    return ;
}
inline void Push_down(int rt , int l , int r) {
    if(tag[rt]) {
        tag[rt << 1] += tag[rt] ;
        tag[rt << 1 | 1] += tag[rt] ;
        int mid = l + r >> 1 ;
        sum[rt << 1] += tag[rt] * (mid - l + 1) ;
        sum[rt << 1 | 1] += tag[rt] * (r - mid) ;
        tag[rt] = 0 ;
        return ;
    }
}
inline void Change(int a , int b , int l , int r , int rt , int val) {
    if(a <= l && r <= b) {
        sum[rt] += val * (r - l + 1) ;
        tag[rt] += val ;
        return ;
    }
    int mid = l + r >> 1 ;
    Push_down(rt , l , r) ;
    if(a <= mid) Change(a , b , l , mid , rt << 1 , val) ;
    if(b > mid) Change(a , b , mid + 1 , r , rt << 1 | 1 , val) ;
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1] ;
    return ;
}
inline int Query(int a , int b , int l , int r , int rt) {
    if(a <= l && r <= b) return sum[rt] ;
    int mid = l + r >> 1 ;
    int ans = 0 ;
    Push_down(rt , l , r) ;
    if(a <= mid) ans += Query(a , b , l , mid , rt << 1) ;
    if(b > mid) ans += Query(a , b , mid + 1 , r , rt << 1 | 1) ;
    return ans ;
}
inline int Query_Range(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    int ans = 0 ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        ans += Query(id[fx] , id[x] , 1 , n , 1) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    ans += Query(id[x] + 1 , id[y] , 1 , n , 1) ;
    return ans ;
}
inline void Change_Range(int x , int y , int val) {
    int fx = top[x] ;
    int fy = top[y] ;
    int ans = 0 ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        Change(id[fx] , id[x] , 1 , n , 1 , val) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    Change(id[x] + 1 , id[y] , 1 , n , 1 , val) ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ; int q = read() ;
    for(register int  i = 1 ; i <= n - 1 ; i ++) {
        int u = read() ;
        int v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    build(1 , n , 1) ;
    for(register int i = 1 ; i <= q ; i ++) {
        register char c = getchar() ;
        for( ; c != 'C' && c != 'Q' && c != 'U' ; c = getchar()) ;
        if(c == 'Q') {
            int x = read() , y = read() ;
            if(Query_Range(x , y)) puts("No") ;
            else puts("Yes") ;
        }
        if(c == 'C') {
            int x = read() , y = read() ;
            Change_Range(x , y , 1) ;
            v.push_back(make_pair(x , y)) ;
        }
        if(c == 'U') {
            int num = read() - 1 ;
            int x = v[num].first ;
            int y = v[num].second ;
            Change_Range(x , y , - 1) ;
        }
    }
    return 0 ;
}

[HAOI2015]树上操作

操作 1 ：把某个节点 x 的点权增加 a 。
操作 2 ：把某个节点 x 为根的子树中所有点的点权都增加 a 。
操作 3 ：询问某个节点 x 到根的路径中所有点的点权和。

很显然是个板子题啊。

// Isaunoya
#include 
using namespace std ;
inline int read() { register int res = 0 ; register int f = 1 ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ; if(c == '-') f = -1 , gc ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res * f ;
}
#define int long long
int n , m , r ;
const int N = 1000000 + 5 ;
struct E{ int v ;int nxt ; } ;
E edge[N << 1] ;
int a[N] ; int fa[N] ; int w[N] ; int id[N] ; int son[N] ;
int cnt = 0 ; int head[N] ; int Add[N << 2] , laz[N << 2] ;
int dep[N] , siz[N] , t[N] ;
inline void Add_Edge(register int u , register int v) { edge[++ cnt].v = v ; edge[cnt].nxt = head[u] ; head[u] = cnt ; return ; }
#define l(x) x << 1
#define r(x) x << 1 | 1
inline void Push_down(register int x , register int len) {
    laz[l(x)] += laz[x] ; laz[r(x)] += laz[x] ;
    Add[l(x)] += laz[x] * (len - (len >> 1)) ; Add[r(x)] += laz[x] * (len >> 1) ;
    laz[x] = 0 ; return ;
}
inline void Build(register int l , register int r , register int rt) {
    if(l == r) { Add[rt] = a[l] ;  return ; }
    register int mid = l + r >> 1 ;
    Build(l , mid , l(rt)) ; Build(mid + 1 , r , r(rt)) ;
    Add[rt] = (Add[l(rt)] + Add[r(rt)])  ;
}
inline void Update(register int a , register int b , register int l  , register int r , register int rt , register int k) {
    if(a <= l and r <= b) { laz[rt] += k ; Add[rt] += k * (r - l + 1) ; }
    else {
        if(laz[rt]) Push_down(rt , r - l + 1) ;
        register int mid = l + r >> 1 ;
        if(a <= mid) Update(a , b , l , mid , l(rt) , k) ;
        if(b > mid) Update(a , b , mid + 1 , r , r(rt) , k) ;
        Add[rt] = (Add[l(rt)] + Add[r(rt)])  ;
    }
}
int res = 0 ;
inline void query(register int a , register int b , register int  l , register int r , register int rt) {
    if(a <= l and r <= b) { res = (res + Add[rt])  ; return ; }
    else {
        if(laz[rt]) Push_down(rt , r - l + 1) ;
        register int mid = l + r >> 1 ;
        if(a <= mid) query(a , b , l , mid , l(rt)) ;
        if(b > mid) query(a , b , mid + 1 , r , r(rt)) ;
    }
}
inline int Query(register int a , register int b , register int l , register int r , register int rt) {
    res = 0 ; query(a , b , l , r , rt) ;
    return res  ;
}
inline void Upd_Range(register int x , register int y , register int k) {
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
         Update(id[t[x]] , id[x] , 1 , n , 1 , k) ;
         x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    Update(id[x] , id[y] , 1 , n , 1 , k) ;
}
inline int Query_Range(register int x , register int y) {
    int ans = 0 ;
    while(t[x] != t[y]) {
        if(dep[t[x]] < dep[t[y]]) swap(x , y) ;
        ans += Query(id[t[x]] , id[x] , 1 , n , 1) ;
        x = fa[t[x]] ;
    }
    if(dep[x] > dep[y]) swap(x , y) ;
    ans += Query(id[x] , id[y] , 1 , n , 1) ;
    return ans ;
}
inline int Qson(register int x) { return Query(id[x] , id[x] + siz[x] - 1 , 1 , n , 1) ; }
inline void Updson(register int x , register int k) { Update(id[x] , id[x] + siz[x] - 1 , 1 , n , 1 , k) ; return ; }
inline void Dfs1(register int x , register int f , register int deep) {
    dep[x] = deep ; fa[x] = f ; siz[x] = 1 ;
    int max_son = -1 ;
    for(register int i = head[x] ; i ; i = edge[i].nxt) {
        register int v = edge[i].v ;
        if(v == f) continue ;
        Dfs1(v , x , deep + 1) ;siz[x] += siz[v] ;
        if(siz[v] > max_son) max_son = siz[v] , son[x] = v ;
    }
}
int tot = 0 ;
inline void Dfs2(register int x , register int tf) {
    id[x] = ++ tot ; a[tot] = w[x] ; t[x] = tf ;
    if(! son[x]) return ;
    Dfs2(son[x] , tf) ;
    for(register int i = head[x] ; i ; i = edge[i].nxt) {
        int v = edge[i].v ;
        if(v == fa[x] or v == son[x]) continue ;
        Dfs2(v , v) ;
    }
}
signed main() {
    n = read() ; m = read() ; r = 1 ;
    for(register int i = 1 ; i <= n ; i ++) w[i] = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() ;
        Add_Edge(u , v) ;
        Add_Edge(v , u) ;
    }
    Dfs1(r , 0 , 1) ; Dfs2(r , r) ; Build(1 , n , 1) ;
    for( ; m -- ; ) {
        register int opt = read() ;
        if(opt == 1) {
            int x = read() , a = read() ;
            Upd_Range(x , x , a) ;
        }
        if(opt == 2) {
            int x = read() , z = read() ;
            Updson(x , z) ;
        }
        if(opt == 3) {
            int x = read() ;
            printf("%lld\n" , Query_Range(x , r)) ;
        }
    }
    return 0 ;
}

上面都是用线段树维护的序列其实树剖不一定要用线段树只要是数据结构都可以
比如说ODT 什么的如果不会ODT也没什么关系你会用线段树当然更好 ODT 是可以卡掉的但是在树上问题通常不容易卡掉。

CF343D Water Tree

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge

int n ;
struct ODT {
    int l , r ;
    mutable int val ;
    bool operator <(const ODT & x) const{
        return l < x.l ;
    }
};
set < ODT > s ;
typedef set < ODT > :: iterator IT ;
inline IT Split(int pos) {
    IT it(-- s.upper_bound({pos , 0 , 0})) ;
    if(it -> l == pos) return it ;
    int L(it -> l) ;
    int R(it -> r) ;
    int Val(it -> val) ;
    s.erase(it) ;
    s.insert({L , pos - 1 , Val}) ;
    return s.insert({pos , R , Val}).first ;
}
inline void Assign(int l , int r , int val) {
    IT itr(Split(r + 1)) ;
    IT itl(Split(l)) ;
    s.erase(itl , itr) ;
    s.insert({l , r , val}) ;
    return ;
}
//===========================================ODT
struct node {
    int v ;
    int nxt ;
} ;
const int N = 500000 + 5 ;
node e[N << 1] ;
int head[N] ;
int cnt = 0 ;
inline void Add(int u ,int v) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ;
    head[u] = cnt ;
    return ;
}
int size[N] ; int d[N] ;
int top[N] ; int idx = 0 ;
int id[N] ; int fa[N] ;
int son[N] ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        d[v] = d[u] + 1 ;
        fa[v] = u ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    } 
}
inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    top[u] = t ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
    }
}
inline void Change_Range(int x) {
    int fx = top[x] ;
    while(fx ^ 1) {
        Assign(id[fx] , id[x] , 0) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    Assign(id[1] , id[x] , 0) ;
}
inline void Query(int x) {
    IT pos(Split(x)) ;
    write(pos -> val) ;
}
signed main() {
#ifndef Online_Judge
//  freopen("testdata.in" , "r" , stdin) ;
//  freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    s.insert({0 , n + 1 , 0}) ;
    for(register int m = read() ; m -- ; ) {
        int opt = read() ;
        if(opt == 1) {
            int v = read() ;
            Assign(id[v] , id[v] + size[v] - 1 , 1) ;
        }
        if(opt == 2) {
            int v = read() ;
            Change_Range(v) ;
        }
        if(opt == 3) {
            int v = read() ;
            Query(id[v]) ;
        }
    }
    return 0 ;
}

[NOI2015]软件包管理器
因为软件之间是有依赖关系的

每次安装软件就把根节点到x软件路径上的值全部变为1
同理每次卸载软件就把x以及它的子树的值变为0

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge

struct node {
    int l ; int r ;
    mutable int val ;
    bool operator < (const node & x) const {
        return l < x.l ;
    }
};
set < node > s ;

#define slt set < node > :: iterator
inline slt Split(int pos) {
    slt it = s.lower_bound((node) {pos}) ;
    if(it != s.end() && it -> l == pos) return it ;
    -- it ;
    int l = it -> l ;
    int r = it -> r ;
    int val = it -> val ;
    s.erase(it) ;
    s.insert({l , pos - 1 , val}) ;
    return s.insert({pos , r , val}).first ;
}
inline int Assign(int l , int r , int val) {
    slt it2 = Split(r + 1) ;
    slt it1 = Split(l) ;
    int sum = 0 ;
    int sum2 = (r - l + 1) * val  ;
    for(slt it = it1 ; it != it2 ; it ++) sum += (it -> r - it -> l + 1) * it -> val ;
    s.erase(it1 , it2) ;
    s.insert({l , r , val}) ;
    return abs(sum - sum2) ;
}
int n ;
struct Node {
    int v ;
    int nxt ;
};
const int N = 1e5 + 10 ;
Node e[N << 1] ;
int cnt = 0 ;
int head[N] ;
inline void Add(int u , int v) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ;
    head[u] = cnt ;
    return ;
}
int top[N] ;
int id[N] ; int size[N] ;
int d[N] ; int idx = 0 ;
int fa[N] ; int son[N] ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt ) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        d[v] = d[u] + 1 ;
        fa[v] = u ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
    return ;
}
inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    top[u] = t ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if((v ^ fa[u]) && (v ^ son[u])) Dfs2(v , v) ;
    }
}
inline int getopt() { string s = "" ;
    register char c = getchar() ;
    while(isspace(c)) c = getchar() ;
    while(! isspace(c)) {
        s += c ;
        c = getchar() ;
    }
    if(s == "install") return 1 ;
    if(s == "uninstall") return 0 ;
}
inline int Change_Range(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    int ans = 0 ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        ans += Assign(id[fx] , id[x] , 1) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    ans += Assign(id[x] , id[y] , 1) ;
    return ans ;
}
inline int Uninstall(int x) {
    return Assign(id[x] , id[x] + size[x] - 1 , 0) ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    s.insert({1 , n + 1 , 0}) ;
    for(register int i = 2 ; i <= n ; i ++) {
        int u = read() ; u ++ ;
        Add(u , i) ;
        Add(i , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    for(register int t = read() ; t -- ; ) {
        int opt = getopt() ;
        if(opt == 1) {
            int x = read() ; x ++ ;
            write(Change_Range(x , 1)) ;
        }
        if(opt == 0) {
            int x = read() ; x ++ ;
            write(Uninstall(x)) ;
        }
    }
    return 0 ;
}

[SDOI2011]染色

这题也是个ODT
不过不同的是这题是区间的颜色数量连续的颜色算一次这样的话线段树还是很难维护的。（应该也可以。）

//Isaunoya
#include
using namespace std ;
inline int read() {
    register int x = 0 ;
    register int f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
int st[105] ;
template < typename T > inline void write(T x , char c = '\n') {
    int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge

struct node {
    int l ;
    int r ;
    mutable int val ;
    bool operator < (const node & x) const {
        return l < x.l ;
    }
};
set < node > s ;

#define slt set < node > :: iterator
inline slt Split(int pos) {
    slt it (-- s.upper_bound({pos})) ;
    if(it -> l == pos) return it ;
    int l = it -> l ;
    int r = it -> r ;
    int val = it -> val ;
    s.erase(it) ;
    s.insert({l , pos - 1 , val}) ;
    return s.insert({pos , r , val}).first ;
}
inline void Assign(int l , int r , int val) {
    slt itr = Split(r + 1) ;
    slt itl = Split(l) ;
    s.erase(itl , itr) ;
    s.insert({l , r , val}) ;
    return ;
}
int n ;
struct Node {
    int v ;
    int nxt ;
};
const int N = 1e5 + 10 ;
int a[N] ;
Node e[N << 1] ;
int cnt = 0 ;
int head[N] ;
inline void Add(int u , int v) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ;
    head[u] = cnt ;
    return ;
}
int top[N] ;
int id[N] ;
int size[N] ;
int d[N] ;
int idx = 0 ;
int fa[N] ;
int son[N] ;
int fst[N] ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt ) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        d[v] = d[u] + 1 ;
        fa[v] = u ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
    return ;
}
inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    top[u] = t ;
    a[idx] = fst[u] ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if((v ^ fa[u]) && (v ^ son[u])) Dfs2(v , v) ;
    }
}
inline int getopt() {
    register char c = getchar() ;
    while(isspace(c)) c = getchar() ;
    return c == 'Q' ;
}
inline void Change_Range(int x , int y , int val) {
    int fx = top[x] ;
    int fy = top[y] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        Assign(id[fx] , id[x] , val) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    Assign(id[x] , id[y] , val) ;
}
#define swap(x , y) x ^= y ^= x ^= y
inline int Query_Range(int x , int y) {
    int ans = 0 ;
    int lasta = 0 ;
    int lastb = 0 ;
    int fx = top[x] ;
    int fy = top[y] ;
    slt itl , itr ;
    while(fx ^ fy) {
        if(d[fx] > d[fy]) {
            itr = Split(id[x] + 1) , itl = Split(id[fx]) ;
            for(-- itr ; ; --itr) {
                if(itr -> val ^ lasta)
                    lasta = itr -> val , ++ ans ;
                if(itr == itl) break;
            }
            x = fa[fx] ;
            fx = top[x] ;
        } else {
//          swap(x , y) , swap(fx , fy) ;
            itr = Split(id[y] + 1) , itl = Split(id[fy]) ;
            for(-- itr ; ; --itr) {
                if(itr -> val ^ lastb)
                    lastb = itr -> val , ++ ans ;
                if(itr == itl) break;
            }
            y = fa[fy] ;
            fy = top[y] ;
        }
    }
    if(id[x] > id[y]) {
        itr = Split(id[x] + 1) , itl = Split(id[y]) ;
        for(-- itr ; ; --itr) {
            if(itr -> val ^ lasta)
                lasta = itr -> val , ++ ans ;
            if(itr == itl) break;
        }
    } else {
        itr = Split(id[y] + 1) , itl = Split(id[x]) ;
        for(-- itr ; ; --itr) {
            if(itr -> val ^ lastb)
                lastb = itr -> val , ++ ans ;
            if(itr == itl) break;
        }
    }
    return ans - (lasta == lastb) ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    int t = read() ;
    for(register int i = 1 ; i <= n ; i ++) fst[i] = read() ;
    for(register int i = 2 ; i <= n ; i ++) {
        int u = read() ;
        int v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    for(register int i = 1 ; i <= n ; i ++) s.insert({i , i , a[i]}) ;
    for( ; t -- ; ) {
        int opt = getopt() ;
        if(opt == 1) {
            int x = read() , y = read() ;
            write(Query_Range(x , y));
        }
        if(opt == 0) {
            int x = read() , y = read() , val = read() ;
            Change_Range(x , y , val) ;
        }
    }
    return 0 ;
}

[SDOI2014]旅行
动态开点。

“CC x c“：城市x的居民全体改信了c教；
“CW x w“：城市x的评级调整为w;
“QS x y“：一位旅行者从城市x出发，到城市y，并记下了途中留宿过的城市的评级总和；
“QM x y“：一位旅行者从城市x出发，到城市y，并记下了途中留宿过的城市的评级最大值。
基本操作还是一样。
如果没有第一个操作是可以树剖+线段树做的但是有了第一个操作就只能用动态开点做了。

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge
int n ;
const int N = 5e5 + 5 ;

int val[N] ;
int cl[N] ;
struct node {
    int v ;
    int nxt ;
};
node e[N << 1] ;
int L[N << 2] , R[N << 2] ;
int head[N] ; int cnt = 0 ;
inline void Add(int u ,int v) {
    e[++ cnt].v = v ;
    e[cnt].nxt = head[u] ; 
    head[u] = cnt ;
    return ;
}
int a[N] ;
int fa[N] ;
int top[N] ;
int id[N] ;
int size[N] ;
int son[N] ;
int d[N] ; int RT[N] ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        fa[v] = u ;
        d[v] = d[u] + 1 ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
}
int idx = 0 ;
inline void Dfs2(int u , int t) {
    top[u] = t ;
    id[u] = ++ idx ;
    a[idx] = u ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
    }
}
int mx[N << 2] ;
int sum[N << 2];

inline void Push_Up(int rt) {
    mx[rt] = max(mx[L[rt]] , mx[R[rt]]) ;
    sum[rt] = sum[L[rt]] + sum[R[rt]] ;
    return ;
}
int c = 0 ;

inline void Modify(int & p , int l , int r , int k , int val) {//开点。
    if(! p) p = ++ c ;
    if(l >= r) {
        mx[p] = sum[p] = val ;
        return ;
    } 
    int mid = l + r >> 1 ;
    if(k <= mid) Modify(L[p] , l , mid , k , val) ;
    else Modify(R[p] , mid + 1 , r , k , val) ;
    Push_Up(p) ;
    if(! sum[p]) p = 0 ;
}
inline int Query_Max(int p , int a , int b , int l , int r) { // 查询
    if(! p) return -1 ;
    if(a <= l && r <= b) return mx[p] ;
    int mid = l + r >> 1 ;
    int ans = - 1 ;
    if(a <= mid) ans = max(ans , Query_Max(L[p] , a , b,  l , mid)) ;
    if(b > mid) ans = max(ans , Query_Max(R[p] , a , b, mid + 1 , r)) ;
    return ans ;
}
inline int Query_Sum(int p , int a , int b , int  l , int r){//查询
    if(! p) return 0 ;
    if(a <= l && r <= b) return sum[p] ;
    int mid = l + r >> 1 ;
    int ans = 0 ;
    if(a <= mid) ans += Query_Sum(L[p] , a , b , l , mid) ;
    if(b > mid) ans += Query_Sum(R[p] , a , b , mid + 1 , r) ;
    return ans ;
}
inline int Max_Range(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    int ans = 0 ;
    int t = cl[x] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        ans = max(ans , Query_Max(RT[t] , id[fx] , id[x] , 1 , idx)) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
    ans = max(ans , Query_Max(RT[t] , id[x] , id[y] , 1 , idx)) ;
    return ans ;
}
inline int Query_Range(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    int ans = 0 ;
    int t = cl[x] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        ans += Query_Sum(RT[t] , id[fx] , id[x] , 1 , idx) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(id[x] > id[y]) swap(x , y) ;
//  cout << ans << endl ;
    ans += Query_Sum(RT[t] , id[x] , id[y] , 1 , idx) ;
//  cout << ans << endl ;
    return ans ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ; int q = read() ;
    for(register int i = 1 ; i <= n ;i ++) {
        val[i] = read() ;
        cl[i] = read() ;
    }
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
//  puts("1") ;
    for(register int i = 1 ; i <= n ; i ++) Modify(RT[cl[a[i]]] , 1 , idx ,  i , val[a[i]]) ;
    for(register int i = 1 ; i <= q ; i ++) {
        register char c = getchar() ;
        for( ; c != 'C' && c != 'Q' ; c = getchar()) ;
        register char c2 = getchar() ;
        if(c == 'C' && c2 == 'C') {
            int c = read() , x = read() ;
            Modify(RT[cl[c]] , 1 , idx , id[c] , 0) ;//删点
            cl[c] = x ;
            Modify(RT[cl[c]] , 1 , idx , id[c] , val[c]) ;//开点
        }
        if(c == 'C' && c2 == 'W') {
            int c = read() , x = read() ;
            val[c] = x ;
            Modify(RT[cl[c]] , 1 , idx , id[c] , val[c]) ; // 修改
        }
        if(c == 'Q' && c2 == 'S') {
            int x = read() , y = read() ;
            write(Query_Range(x , y)) ;
        }
        if(c == 'Q' && c2 == 'M') {
            int x = read() , y  =read() ;
            write(Max_Range(x , y)) ;
        }
    }
    return 0 ;
}

Count on a tree

给定一棵N个节点的树，每个点有一个权值，对于M个询问(u,v,k)，你需要回答u xor lastans和v这两个节点间第K小的点权。其中lastans是上一个询问的答案，初始为0，即第一个询问的u是明文。
强制在线，那么考虑静态主席树求区间第k小。。还是一样的套路。。如果不会主席树建议 -> HERE

//Isaunoya
#include
using namespace std ;
inline int read() { register int x = 0 ; register int f = 1 ; register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
} int st[105] ;
template < typename T > inline void write(T x , char c = '\n') { int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge
const int N = 1e5 + 10 ;
const int M = N << 5 ;
int n , q ; int m ;
int sum[M] , L[M] , R[M] ;
int a[N] , b[N] , rt[N] ;
struct node{
    int v ;
    int nxt ;
};
node e[N << 1] ;
int head[N] ;
int fa[N] , size[N] , d[N] , son[N] , top[N] ;
int cnt =  0 ; 
inline void Add(int u , int v) {
    e[ ++ cnt] . v = v ;
    e[ cnt] . nxt = head[u] ;
    head[u] = cnt ;
    return ;
}
int tot = 0 ;
inline void Update(int last , int & now , int l , int r , int x) { // 动态开点 主席树基操
    sum[now = ++ tot] = sum[last] + 1 ;
    if(l == r) return ;
    int mid = l + r >> 1 ;
    if(x <= mid) R[now] = R[last] , Update(L[last] , L[now] , l , mid , x) ;
    else L[now] = L[last] , Update(R[last] , R[now] , mid + 1 , r , x) ;
    return ;
}
inline int Query(int a , int b , int lca ,int lca_fa , int l , int r , int k) { // 求 k 小…
    if(l >= r) return l ;
    int x = sum[L[a]] + sum[L[b]] - sum[L[lca]] - sum[L[lca_fa]] ;
    int mid = l + r >> 1 ;
    if(x >= k) return Query(L[a] , L[b] , L[lca] , L[lca_fa] , l , mid , k) ;
    else return Query(R[a] , R[b] , R[lca] , R[lca_fa] , mid + 1 , r , k - x) ;
}

inline void Dfs(int u) {
    size[u] = 1 ;
    Update(rt[fa[u]] , rt[u] , 1 , m , a[u]) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        fa[v] = u  ;
        d[v] = d[u] + 1 ;
        Dfs(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
}
inline void Dfs2(int u , int t) {
    top[u] = t ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
    }
}
inline int Lca(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(d[x] > d[y]) swap(x , y) ;
    return x ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() , q = read() ;
    for(register int i = 1 ; i <= n ; i ++) a[i] = read() ;
    for(register int i = 1 ; i <= n ; i ++) b[i] = a[i] ;
    sort(b + 1 , b + n + 1) ;
    m = unique(b + 1 , b + 1 + n) - b - 1 ;
    for(register int i = 1 ; i <= n ; i ++) 
        a[i] = lower_bound(b + 1 , b + m + 1 , a[i]) - b ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u = read() , v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs(1) ;
    Dfs2(1 , 1) ;
    int ans = 0 ;
    for(register int i = 1 ; i <= q ; i ++) {
        int x = read() ^ ans , y = read() ;
        int lca = Lca(x , y) ;
        int z = read() ;
        write(ans = b[Query(rt[x] , rt[y] , rt[lca] , rt[fa[lca]] , 1 , m , z)]) ;
    }
    return 0 ;
}

[Vani有约会]雨天的尾巴

对于这题是一个线段树合并的问题
线段树合并例题 -> sol
递归求解合并线段树的信息。

//Isaunoya
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include
using namespace std ;
inline int read() {
    register int x = 0 ;
    register int f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
int st[105] ;
template < typename T > inline void write(T x , char c = '\n') {
    int tp = 0 ;
    if(x == 0) return (void) puts("0") ;
    if(x < 0) putchar('-') , x = -x ;
    for( ; x ; x /= 10) st[++ tp] = x % 10 ;
    for( ; tp ; tp --) putchar(st[tp] + '0') ;
    putchar(c) ;
}
//#define Online_Judge
int n , m ;
const int N = 1e5 + 10 ;
int lc[N << 6] ;
int rc[N << 6] ;
int rt[N << 6] ;
int mx[N << 6] , id[N << 6] ;
int cnt = 0 ;
inline void Push_up(int rt) {
    if(mx[lc[rt]] >= mx[rc[rt]]) {
        mx[rt] = mx[lc[rt]] ;
        id[rt] = id[lc[rt]] ;
    } else {
        mx[rt] = mx[rc[rt]] ;
        id[rt] = id[rc[rt]] ;
    }
}
inline int Merge(int a , int b , int  l , int r) {
    if(! a || ! b) return a | b ;
    if(l == r) {
        mx[a] += mx[b] , id[a] = l ;
        return a ;
    }
    int mid = l + r >> 1 ;
    lc[a] = Merge(lc[a] , lc[b] , l , mid) ;
    rc[a] = Merge(rc[a] , rc[b] , mid + 1 , r) ;
    return Push_up(a) , a ;
}
inline void Insert(int & p , int l , int r , int pos , int v) {
    if(! p) p = ++ cnt ;
    if(l == r) {
        id[p] = l ;
        mx[p] += v ;
        return ;
    }
    int mid = l + r >> 1 ;
    if(pos <= mid) Insert(lc[p] , l , mid , pos , v) ;
    else Insert(rc[p] , mid + 1 , r , pos , v) ;
    Push_up(p) ;
    return ;
}
struct node {
    int v ;
    int nxt ;
};
int tot = 0 ;
int head[N] ;
node e[N << 1] ;
inline void Add(int u , int v) {
    e[++ tot].v = v ;
    e[tot].nxt = head[u] ;
    head[u] = tot ;
    return ;
}
int top[N] , fa[N] ;
int d[N] , idx[N] ;
int size[N] , son[N] ;
int Idx = 0 ;
inline void Dfs1(int u) {
    size[u] = 1 ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa[u]) continue ;
        fa[v] = u ;
        d[v] = d[u] + 1 ;
        Dfs1(v) ;
        size[u] += size[v] ;
        if(size[v] > size[son[u]]) son[u] = v ;
    }
}
inline void Dfs2(int u , int t) {
    idx[u] = ++ Idx ;
    top[u] = t ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt) {
        int v = e[i].v ;
        if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
    }
}
inline int GetLca(int x , int y) {
    int fx = top[x] ;
    int fy = top[y] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(fx , fy) , swap(x , y) ;
        x = fa[fx] ;
        fx = top[x] ;
    }
    if(d[x] > d[y]) swap(x , y) ;
    return x ;
}
int ans[N] ;
inline void GetAns(int u , int fa) {
    for(register int i = head[u ] ; i ; i  = e[i].nxt) {
        int v = e[i].v ;
        if(v == fa) continue ;
        GetAns(v , u) ;
        rt[u] = Merge(rt[u] , rt[v] , 1 , N) ;
    }
    ans[u] = id[rt[u]] ;
    if(mx[rt[u]] == 0) ans[u] = 0 ;
}
signed main() {
#ifdef Online_Judge
    freopen("testdata.in" , "r" , stdin) ;
    freopen("testdata2.out" , "w" , stdout) ;
#endif
    n = read() ;
    m = read() ;
    for(register int i = 1 ; i <= n - 1 ; i ++) {
        int u , v ;
        u = read() , v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    Dfs1(1) ;
    Dfs2(1 , 1) ;
    for(register int i = 1 ; i <= m ; i ++) {
        int x = read() , y = read() , z = read() ;
        int lca = GetLca(x , y) ;
        Insert(rt[lca] , 1 , N , z , - 1) ;
        Insert(rt[fa[lca]] , 1 , N , z , - 1) ;
        Insert(rt[x] , 1 , N , z , 1) ;
        Insert(rt[y] , 1 , N , z , 1) ;
    }
    GetAns(1 , 0) ;
    for(register int i = 1 ; i <= n ; i ++) write(ans[i]) ;
    return 0 ;
}

这里还有一个重要操作：换根
换根是一个比较重要的操作 "换根"不一定要重新DFS以及建树只需要根据根所在的位置和查询的位置分类讨论就可以了。
但是你需要求一个 k - 1 级祖先(也就是最上面的那个的儿子节点) 所以需要一种倍增的想法

[BZOJ3083][遥远的国度]

//Isaunoya
#include
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
    register int x = 0 , f = 1 ;
    register char c = getchar() ;
    for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
    return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
    return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
    return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
    return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
    int ans = 1 ;
    for( ; y ; y >>= 1 , x = (x * x) % Mod)
        if(y & 1) ans = (ans * x) % Mod ;
    return ans ;
}
struct node {
    int v , nxt ;
} ;
int n , m ;
const int N = 100000 + 5 ;
int a[N] ;
node e[N<<1];int head[N],cnt=0;
inline void Add(int u , int v){
    e[++cnt].v = v ;
    e[cnt].nxt = head[u] ;
    head[u] = cnt ;
}
int fa[N][22], size[N] , son[N] , d[N] ;
inline void Dfs(int u) {
    size[u] = 1 ;
    for(register int i = 1 ; i <= 20 ; i ++) { // 倍增预处理
        fa[u][i] = fa[fa[u][i - 1]][i - 1] ;
        if(! fa[u][i]) break ;
    }
    for(register int i = head[u] ; i ; i = e[i].nxt){
        int v = e[i].v ;
        if(v == fa[u][0]) continue ;
        fa[v][0] = u ;
        d[v] = d[u] + 1 ;
        Dfs(v) ;
        size[u] += size[v] ;
        if(size[son[u]] < size[v]) son[u] = v ;
    }
}
int id[N] , idx = 0 ;
int fst[N] , top[N] ;
inline void Dfs2(int u , int t) {
    id[u] = ++ idx ;
    fst[idx] = a[u] ;
    top[u] = t ;
    if(! son[u]) return ;
    Dfs2(son[u] , t) ;
    for(register int i = head[u] ; i ; i = e[i].nxt){
        int v = e[i].v ;
        if((v ^ fa[u][0]) && (v ^ son[u])) Dfs2(v , v) ;
    }
    return ;
}
int mn[N << 2] ;
int tag[N << 2] ;
inline void build(int l , int r , int rt) {
    tag[rt] = 0 ;
    if(l == r) { mn[rt] = fst[l] ; return ; }
    int mid = l + r >> 1 ;
    build(l , mid , rt << 1) ;
    build(mid + 1 , r , rt << 1 | 1) ;
    mn[rt] = min(mn[rt << 1] , mn[rt << 1 | 1]) ;
}
inline void Push_down(int rt) {
    if(! tag[rt]) return ;
    mn[rt << 1] = mn[rt << 1 | 1] = tag[rt << 1] = tag[rt << 1 | 1] = tag[rt] ;
    return (void)(tag[rt]=0) ;
}
inline void Change(int a , int b , int  l, int r , int rt , int val) {
    if(a <= l && r <= b) {
        mn[rt] = tag[rt] = val ;
        return ;
    } Push_down(rt) ;
    int mid = l + r >> 1 ;
    if(a <= mid) Change(a , b , l , mid , rt << 1 , val) ;
    if(b > mid) Change(a , b , mid + 1 , r , rt << 1 | 1 , val) ;
    mn[rt] = min(mn[rt << 1] , mn[rt << 1 | 1]) ;
}
inline int Query(int a , int b , int  l, int r , int rt) {
    if(a <= l && r <= b) return mn[rt] ;
    Push_down(rt) ;
    int mid = l + r >> 1 ;
    int ans = INT_MAX ;
    if(a <= mid) cmin(ans , Query(a , b , l , mid , rt << 1 )) ;
    if(b > mid) cmin(ans , Query(a , b , mid + 1 , r , rt << 1 | 1)) ;
    return ans ;
}
inline void Change_Range(int x , int y , int val) {
    int fx = top[x] , fy = top[y] ;
    while(fx ^ fy) {
        if(d[fx] < d[fy]) swap(x , y) , swap(fx , fy) ;
        Change(id[fx] , id[x] , 1 , n , 1 , val) ;
        x = fa[fx][0] ;
        fx = top[x] ;
    }
    if(d[x] > d[y]) swap(x , y) ;
    Change(id[x] , id[y] , 1 , n , 1 , val) ;
}
inline int getfa(int x , int k) { // k 级祖先
    for(register int i = 20 ; i >= 0 ; i --)
        if(k >= (1 << i)) k ^= (1 << i) , x = fa[x][i] ;
    return x ;
}
int root = 1 ;
inline void getans(int x) { // 分类讨论
    if(x == root) {//与根相同就是全局最大值即mn[1]
        printf("%lld\n" , mn[1]) ;
        return ;
    }
    int y = 0 ;
    int p , q ;
    if(d[x] < d[root] && fa[y = getfa(root , d[root] - d[x] - 1)][0] == x) {
        p = Query(1 , id[y] - 1 , 1 , n , 1) ;
        if(id[y] + size[y] <= n) q = Query(id[y] + size[y] , n , 1 , n , 1) ;
        else q = INT_MAX ;
        printf("%lld\n" , min(p , q)) ;
    }
    else printf("%lld\n" , Query(id[x] , id[x] + size[x] - 1 , 1 , n , 1)) ; // 子树中
}
signed main() {
    n = read() ; m = read() ;
    for(register int i = 1 ; i < n ; i ++) {
        int u = read() , v = read() ;
        Add(u , v) ;
        Add(v , u) ;
    }
    for(register int i = 1 ; i <= n ; i ++) a[i] = read() ;
    Dfs(1) ;
    Dfs2(1 , 0) ;
    root = read() ;
    build(1 , n , 1) ;
    for(register int i = 1 ; i <= m ; i ++) {
        int opt = read() ;
        if(opt == 1) {
            root = read() ;
        }
        if(opt == 2) {
            int x = read() , y = read() , val = read() ;
            Change_Range(x , y , val) ;
        }
        if(opt == 3) {
            int x = read() ;
            getans(x) ;
        }
    }
    return 0 ;
}

你可能感兴趣的:(树链剖分(从入门到入土。))

android系统selinux中添加新属性property 辉色投像
1.定位/android/system/sepolicy/private/property_contexts声明属性开头：persist.charge声明属性类型：u:object_r:system_prop:s0图12.定位到android/system/sepolicy/public/domain.te删除neverallow{domain-init}default_prop:property
想家爆米花机
也许不同于大家对家乡的思念，我对家乡甚至是疯狂的不舍。还未踏出车站就感觉到幸福，我享受这里的夕阳、这里的浓烈柴火味、这里每一口家常菜。我是宅女，我贪恋家的安逸。刚刚踏出大学校门，初出茅庐，无法适应每年只能国庆和春节回家。我焦虑、失眠、无端发脾气，是无法适应工作的节奏，是无法接受我将一步步离开家乡的事实。我不想承认自己胸无大志，选择再次踏上征程。图片发自App
element实现动态路由+面包屑软件技术NINI vue案例 vue.js 前端
el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
2021年12月19日，春蕾教育集团团建活动感受——黄晓丹黄错错加油
感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
爬山后遗症璃绛
爬山，攀登，一步一步走向制高点，是一种挑战。成功抵达是一种无法言语的快乐，在山顶吹吹风，看看风景，这是从未有过的体验。然而，爬山一时爽，下山腿打颤，颠簸的路，一路向下走，腿部力量不够，走起来抖到不行，停不下来了！第二天必定腿疼，浑身酸痛，坐立难安！
《策划经理回忆录之二》路基雅虎
话说三年变六年，飘了，飘了……眨眼，2013年5月，老吴回到了他的家乡——油城从新开启他的工作幻想症生涯。很庆幸，这是一家很有追求，同时敢于尝试的，且实力不容低调的新星房企——金源置业(前身泰源置业)更值得庆幸的是第一个盘就是油城十路的标杆之一:金源盛世。2013年5月，到2015年11月，两年的陪伴，迎来了一场大爆发。2000个筹，5万/筹，直接回笼1个亿！！！这……让我开始认真审视这座看似五线
Long类型前后端数据不一致 igotyback 前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
30天风格练习-DAY2 黄希夷
Day2（重义）在一个周日/一周的最后一天，我来到位于市中心/市区繁华地带的一家购物中心/商场，中心内人很多/熙熙攘攘。我注意到/看见一个独行/孤身一人的年轻女孩/，留着一头引人注目/长过腰际的头发，上身穿一件暗红色/比正红色更深的衣服/穿在身体上的东西。走下扶梯的时候，她摔倒了/跌向地面，在她正要站起来/让身体离开地面的时候，过长/超过一般人长度的头发被支撑身体/躯干的手掌压/按在下面，她赶紧用
开心蒋泳频
从无比抗拒来上课到接受，感动，收获～看着波哥成长，晶晶幸福笑容满面。感觉自己做的事情很有意义，很开心！还有3个感召目标就是还有三个有缘人，哈哈。明天感召去明日计划：8：30-11：00小公益11：00-21点上班，感召图片发自App图片发自App图片发自App
每日一题——第八十四题互联网打工人no1 C语言程序设计每日一练 c语言
题目：编写函数1、输入10个职工的姓名和职工号2、按照职工由大到小顺序排列，姓名顺序也随之调整3、要求输入一个职工号，用折半查找法找出该职工的姓名#define_CRT_SECURE_NO_WARNINGS#include#include#defineMAX_EMPLOYEES10typedefstruct{intid;charname[50];}Empolyee;voidinputEmploye
每日一题——第八十二题互联网打工人no1 C语言程序设计每日一练 c语言
题目：将一个控制台输入的字符串中的所有元音字母复制到另一字符串中#include#include#include#include#defineMAX_INPUT1024boolisVowel(charp);intmain(){charinput[MAX_INPUT];charoutput[MAX_INPUT];printf("请输入一串字符串：\n");fgets(input,sizeof(inp
第四天旅游线路预览——从换乘中心到喀纳斯湖陟彼高冈yu 基于Google earth studio 的旅游规划和预览旅游
第四天：从贾登峪到喀纳斯风景区入口，晚上住宿贾登峪；换乘中心有4路车，喀纳斯①号车，去喀纳斯湖，路程时长约5分钟；将上面的的行程安排进行动态展示，具体步骤见”Googleearthstudio进行动态轨迹显示制作过程“、“Googleearthstudio入门教程”和“Googleearthstudio进阶教程“相关内容，得到行程如下所示：Day4-2-480p
从鸡肉高汤到记忆的魔法再到有效提示的艺术步子哥人工智能
还记得小时候那些天马行空的白日梦吗？也许只要按下键盘上的某个神奇组合，电脑就会发出滴滴的声响，一个隐藏的世界突然在你眼前展开，让你获得超凡的能力，摆脱平凡的生活。这听起来像是玩过太多电子游戏的幻想，但实际上，间隔重复系统给人的感觉惊人地相似。在最佳状态下，这些系统就像魔法一样神奇。本文将以一个看似平凡的鸡肉高汤食谱为例，深入浅出地探讨如何编写有效的间隔重复提示，让你像掌握烹饪技巧一样轻松地掌握记忆
谁家酒器最绝唱，藏在酒厂人未知？景阳冈酒厂先秦藏品大揭秘李虓酒评论
文/王赛时中国的酒器酒具历史久远，举世闻名。从北京的故宫博物院、中国国家博物馆，到世界各国的大型博物馆，都以能够收藏中国古代酒具而夸耀。但很少有人知道，在山东阳谷景阳冈酒厂，默默地收藏了两千件中国酒器。这些酒器，就封藏在景阳冈的酒道馆里。其中有一些青铜酒器，一睡就是三、四千年，堪称无声国宝，堪作无字史书！今天，我将引领诸位首先窥视一下景阳冈酒道馆的9件先秦藏品，你自己来说震撼不震撼。提示：这只是景
下载github patch到本地小米人er 我的博客 git patch
以下是几种从GitHub上下载以.patch结尾的补丁文件的方法：通过浏览器直接下载打开包含该.patch文件的GitHub仓库。在仓库的文件列表中找到对应的.patch文件。点击该文件，浏览器会显示文件的内容，在页面的右上角通常会有一个“Raw”按钮，点击它可以获取原始文件内容。然后在浏览器中使用快捷键（如Ctrl+S或者Command+S）将原始文件保存到本地，选择保存的文件名并确保后缀为.p
18-115 一切思考不能有效转化为行动，都TM是扯淡！成长时间线
7月25号写了一篇关于为什么会断更如此严重的反思，然而，之后日更仅仅维持了一周，又出现了这次更严重的现象。从8月2号到昨天8月6号，5天！又是5天没有更文！虽然这次断更时间和上次一样，那为什么说这次更严重？因为上次之后就分析了问题的原因，以及应该如何解决，按理说应该会好转，然而，没过几天严重断更的现象再次出现，想想，经过反思，问题依然没有解决与改变，这让我有些担忧。到底是哪里出了问题，难道我就真的
山东大学小树林支教调研团青青仓木队——翟晓楠山东大学青青仓木队
过了半年，又一次启程，又一次回到支教的初心之地。比起上一次的试探与不安，我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同，半个学期中，身体上的，心理上的，太多的逆境让我变得步履维艰，曲曲折折，弯弯绕绕，我仿佛打不起精神，没有胃口，没有动力。感觉走的不顺畅的时候，支教这个旅程，给了我力量。自告奋勇承担起队长这一职务的我，从组织时的复杂和困难的经历，协调各种问题，从无到有，和校长和队
《中华小厨师》单行VS爱藏：姜是老的辣，书是新的好 cicoky
《汉书·郦食其传》有曰：“王者以民为天，而民以食为天。”自古以来，吃饱饭是每一个人的基本要求，而吃好饭却是每一个人的最终追求。于是，厨师这一职业孕育而生，其渊源之久，甚至可追溯到4000年前的奴隶时代。职业本身无贵贱，但职业能力却有高低之分。所以一家餐馆生意好不好，厨师的水平决定一切，而站在所有厨师顶端的就被称之为“特级厨师”。今天要说的就是一个关于“特级厨师刘昴星”的故事。连载历程1995年第4
万物难度不度己边度512
你好，陌生人！你是否有过迷茫，在别人的面前自己却不曾展示！你是否自己承担着所有的痛苦，却又笑对人生！你是否在很多时候想找人诉说，翻开手机却发现，手机里面空无一人！你是否有很多事情想做，最后却因你自己拖延，最后发现自己什么都做不了！对没有错，我的名字就叫你是否！不要怀疑！不要悲伤！我们的生活可是还有很到要继续的呢！还有很多那个人，很多地方我们都没有去过！所以我们已经没有退路了！那就继续向前吧！加油！
从0到500+，我是如何利用自媒体赚钱？一列脚印
运营公众号半个多月，从零基础的小白到现在慢慢懂了一些运营的知识。做好公众号是很不容易的，要做很多事情；排版、码字、引流…通通需要自己解决，业余时间全都花费在这上面涨这么多粉丝是真的不容易，对比知乎大佬来说，我们这种没资源，没人脉，还没钱的小透明来说，想要一个月涨粉上万，怕是今天没睡醒（不过你有的方法，算我piapia打脸）至少我是清醒的，自己慢慢努力，实现我的万粉目标！大家快来围观、支持我吧！孩子
凤凰公园吴侬暖语sym
凤凰公园距离我们家880米，大概步行12分钟就到了，这是我们每天饭后散步或者闲暇时的去处。现在夏季徬晚时分广场舞大妈们总是热情非凡，那里的大门口就是一个好地方，每天总有两拨人在那踩着节奏翩翩起舞呢！而且一路上，从我们小区到公园，或者从昆仑西苑沿河到公园，都是饭后锻炼的人们，川流不息，老人小孩，年轻人，…！哪哪都是。最早家乡的公园，所有公园都是要收门票的，那时候也就是休息天会有人花钱去转转，平时一般
把握“三度”打造“三有”干部队伍辛德瑞拉卡卡卡
“胜败兴亡之分，不得不归咎于人事也”。干部队伍建设工作的好坏，关系到党和国家的发展全局。近日，新疆维吾尔自治区党委书记马兴瑞在部分党群单位走访调研时强调，要努力培养造就忠诚干净担当的高素质专业化干部队伍。各级组织部门应当在培养选拔干部、吸收优秀青年到党内来、培养造就优秀人才上下功夫，切实增强干部投身实践、解决问题、推进工作的能力，着力打造高素质专业化干部队伍。“天生我材必有用”，增强选育有“准度”
git - Webhook让部署自动化大猪大猪
我们现在有一个需求，将项目打包上传到gitlab或者github后，程序能自动部署，不用手动地去服务器中进行项目更新并运行，如何做到？这里我们可以使用gitlab与github的挂钩，挂钩的原理就是，每当我们有请求到gitlab与github服务器时，这时他俩会根据我们配置的挂钩地扯进行访问，webhook挂钩程序会一直监听着某个端口请求，一但收到他们发过来的请求，这时就知道用户有请求提交了，这时
libyuv之linux编译 jaronho Linux linux 运维服务器
文章目录一、下载源码二、编译源码三、注意事项1、银河麒麟系统（aarch64）（1）解决armv8-a+dotprod+i8mm指令集支持问题（2）解决armv9-a+sve2指令集支持问题一、下载源码到GitHub网站下载https://github.com/lemenkov/libyuv源码，或者用直接用git克隆到本地，如：gitclonehttps://github.com/lemenko
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
怎么做淘客赚钱(2022最新免费淘客盈利的方法) 高省_飞智666600
很多人都不知道什么是淘宝客，今天小编为大家解答一下吧。淘宝客，现在简称淘客，是时下比较流行的一个词语，特质为淘宝店推广商品获取提成的人，这些人没有自己的产品，只是在淘宝里面选择适合自己的产品，在自己比较熟悉的领域推广，把产品卖出去之后，会从淘宝店家那里获得百分之五到百分之五十左右的佣金。淘宝客付出的是什么呢？时间。你需要花时间去选适合自己推广的产品，需要花时间去选自己的推广方法，如果你打算自己做个
数据仓库——维度表一致性墨染丶eye 背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕，完整连接为：数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看，当一系列星型模型共享一组公共维度时，所涉及的维度称为一致性维度。当维度表存在不一致时，短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别，因为维度的差别，分析工作涉及的领域从简单到复杂，但是都是通过复杂的报表来弥补设计
心有蓝天白云，爱情便会晴空万里，然后有花香有鸟鸣有美好的未来曹十二吖
丁南的婚姻，来自于一场她对生命的对比。她曾经说过，当她最爱的母亲用生命去逼迫她结婚的时候，她曾一度不理解到愤怒，甚至于想过用轻生来对抗母亲的不理智。庆幸的是，丁南是一个自我调节能力非常强的人，她想如果我连死亡都不怕，还怕不能经营好一段婚姻吗？抱着这样的念头，24年没有谈过恋爱的她，用短短三个月的时间，完成了少女到女人的蜕变。她曾经说过：“我要把自己最珍贵的东西留给自己命中注定的那个人。”闺蜜几人中
ARM驱动学习之基础小知识 JT灬新一 ARM 嵌入式 arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购（能不能买到，价格）–原理图（涉及到稳定性）•layout画板工程师–layout（封装、布局，布线，log）（涉及到稳定性）–焊接的一部分工作（调试阶段板子的焊接）•驱动工程师–驱动，原理图，layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案，原理图(网表)–layout工程师（gerber文件）–PCB板
C++菜鸟教程 - 从入门到精通第二节 DreamByte c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
算法单链的创建与删除换个号韩国红果果 c 算法
先创建结构体 struct student { int data; //int tag;//标记这是第几个 struct student *next; }; // addone 用于将一个数插入已从小到大排好序的链中 struct student *addone(struct student *h,int x){ if(h==NULL) //??????
《大型网站系统与Java中间件实践》第2章读后感白糖_ java中间件
断断续续花了两天时间试读了《大型网站系统与Java中间件实践》的第2章，这章总述了从一个小型单机构建的网站发展到大型网站的演化过程---整个过程会遇到很多困难，但每一个屏障都会有解决方案，最终就是依靠这些个解决方案汇聚到一起组成了一个健壮稳定高效的大型系统。看完整章内容，
zeus持久层spring事务单元测试 deng520159 java DAO spring jdbc
今天把zeus事务单元测试放出来,让大家指出他的毛病, 1.ZeusTransactionTest.java 单元测试 package com.dengliang.zeus.webdemo.test; import java.util.ArrayList; import java.util.List; import org.junit.Test; import
Rss 订阅开发周凡杨 html xml 订阅 rss 规范
RSS是 Really Simple Syndication的缩写（对rss2.0而言，是这三个词的缩写，对rss1.0而言则是RDF Site Summary的缩写，1.0与2.0走的是两个体系）。 RSS
分页查询实现 g21121 分页查询
在查询列表时我们常常会用到分页，分页的好处就是减少数据交换，每次查询一定数量减少数据库压力等等。按实现形式分前台分页和服务器分页：前台分页就是一次查询出所有记录，在页面中用js进行虚拟分页，这种形式在数据量较小时优势比较明显，一次加载就不必再访问服务器了，但当数据量较大时会对页面造成压力，传输速度也会大幅下降。服务器分页就是每次请求相同数量记录，按一定规则排序，每次取一定序号直接的数据
spring jms异步消息处理 510888780 jms
spring JMS对于异步消息处理基本上只需配置下就能进行高效的处理。其核心就是消息侦听器容器，常用的类就是DefaultMessageListenerContainer。该容器可配置侦听器的并发数量，以及配合MessageListenerAdapter使用消息驱动POJO进行消息处理。且消息驱动POJO是放入TaskExecutor中进行处理，进一步提高性能，减少侦听器的阻塞。具体配置如下：
highCharts柱状图布衣凌宇 hightCharts 柱图
第一步：导入 exporting.js,grid.js,highcharts.js;第二步：写controller @Controller@RequestMapping(value="${adminPath}/statistick")public class StatistickController { private UserServi
我的spring学习笔记2-IoC（反向控制依赖注入） aijuans spring mvc Spring 教程 spring3 教程 Spring 入门
IoC（反向控制依赖注入）这是Spring提出来了，这也是Spring一大特色。这里我不用多说，我们看Spring教程就可以了解。当然我们不用Spring也可以用IoC，下面我将介绍不用Spring的IoC。 IoC不是框架，她是java的技术，如今大多数轻量级的容器都会用到IoC技术。这里我就用一个例子来说明：如：程序中有 Mysql.calss 、Oracle.class 、SqlSe
TLS java简单实现 antlove java ssl keystore tls secure
1. SSLServer.java package ssl; import java.io.FileInputStream; import java.io.InputStream; import java.net.ServerSocket; import java.net.Socket; import java.security.KeyStore; import
Zip解压压缩文件百合不是茶 Zip格式解压 Zip流的使用文件解压
ZIP文件的解压缩实质上就是从输入流中读取数据。Java.util.zip包提供了类ZipInputStream来读取ZIP文件,下面的代码段创建了一个输入流来读取ZIP格式的文件; ZipInputStream in = new ZipInputStream(new FileInputStream(zipFileName)); &n
underscore.js 学习（一） bijian1013 JavaScript underscore
工作中需要用到underscore.js，发现这是一个包括了很多基本功能函数的js库，里面有很多实用的函数。而且它没有扩展 javascript的原生对象。主要涉及对Collection、Object、Array、Function的操作。学
java jvm常用命令工具——jstatd命令(Java Statistics Monitoring Daemon) bijian1013 java jvm jstatd
1.介绍 jstatd是一个基于RMI（Remove Method Invocation）的服务程序，它用于监控基于HotSpot的JVM中资源的创建及销毁，并且提供了一个远程接口允许远程的监控工具连接到本地的JVM执行命令。 jstatd是基于RMI的，所以在运行jstatd的服务
【Spring框架三】Spring常用注解之Transactional bit1129 transactional
Spring可以通过注解@Transactional来为业务逻辑层的方法(调用DAO完成持久化动作)添加事务能力，如下是@Transactional注解的定义： /* * Copyright 2002-2010 the original author or authors. * * Licensed under the Apache License, Version
我(程序员)的前进方向 bitray 程序员
作为一个普通的程序员,我一直游走在java语言中,java也确实让我有了很多的体会.不过随着学习的深入,java语言的新技术产生的越来越多,从最初期的javase,我逐渐开始转变到ssh,ssi,这种主流的码农,.过了几天为了解决新问题,webservice的大旗也被我祭出来了,又过了些日子jms架构的activemq也开始必须学习了.再后来开始了一系列技术学习,osgi,restful.....
nginx lua开发经验总结 ronin47
使用nginx lua已经两三个月了，项目接开发完毕了，这几天准备上线并且跟高德地图对接。回顾下来lua在项目中占得必中还是比较大的，跟PHP的占比差不多持平了，因此在开发中遇到一些问题备忘一下 1：content_by_lua中代码容量有限制，一般不要写太多代码，正常编写代码一般在100行左右（具体容量没有细心测哈哈，在4kb左右），如果超出了则重启nginx的时候会报 too long pa
java-66-用递归颠倒一个栈。例如输入栈{1,2,3,4,5}，1在栈顶。颠倒之后的栈为{5,4,3,2,1}，5处在栈顶 bylijinnan java
import java.util.Stack; public class ReverseStackRecursive { /** * Q 66.颠倒栈。 * 题目：用递归颠倒一个栈。例如输入栈{1,2,3,4,5}，1在栈顶。 * 颠倒之后的栈为{5,4,3,2,1}，5处在栈顶。 *1. Pop the top element *2. Revers
正确理解Linux内存占用过高的问题 cfyme linux
Linux开机后，使用top命令查看，4G物理内存发现已使用的多大3.2G，占用率高达80%以上： Mem: 3889836k total, 3341868k used, 547968k free, 286044k buffers Swap: 6127608k total,&nb
[JWFD开源工作流]当前流程引擎设计的一个急需解决的问题 comsci 工作流
当我们的流程引擎进入IRC阶段的时候，当循环反馈模型出现之后，每次循环都会导致一大堆节点内存数据残留在系统内存中，循环的次数越多，这些残留数据将导致系统内存溢出，并使得引擎崩溃。。。。。。而解决办法就是利用汇编语言或者其它系统编程语言，在引擎运行时，把这些残留数据清除掉。
自定义类的equals函数 dai_lm equals
仅作笔记使用 public class VectorQueue { private final Vector<VectorItem> queue; private class VectorItem { private final Object item; private final int quantity; public VectorI
Linux下安装R语言 datageek R语言 linux
命令如下：sudo gedit /etc/apt/sources.list1、deb http://mirrors.ustc.edu.cn/CRAN/bin/linux/ubuntu/ precise/ 2、deb http://dk.archive.ubuntu.com/ubuntu hardy universesudo apt-key adv --keyserver ke
如何修改mysql 并发数(连接数)最大值 dcj3sjt126com mysql
MySQL的连接数最大值跟MySQL没关系，主要看系统和业务逻辑了方法一：进入MYSQL安装目录打开MYSQL配置文件 my.ini 或 my.cnf查找 max_connections=100 修改为 max_connections=1000 服务里重起MYSQL即可　　方法二：MySQL的最大连接数默认是100客户端登录：mysql -uusername -ppass
单一功能原则 dcj3sjt126com 面向对象的程序设计软件设计编程原则
单一功能原则[ 编辑] SOLID 原则单一功能原则开闭原则 Liskov代换原则接口隔离原则依赖反转原则查论编在面向对象编程领域中，单一功能原则（Single responsibility principle）规定每个类都应该有
POJO、VO和JavaBean区别和联系 fanmingxing VO POJO javabean
POJO和JavaBean是我们常见的两个关键字，一般容易混淆，POJO全称是Plain Ordinary Java Object / Plain Old Java Object，中文可以翻译成：普通Java类，具有一部分getter/setter方法的那种类就可以称作POJO，但是JavaBean则比POJO复杂很多，JavaBean是一种组件技术，就好像你做了一个扳子，而这个扳子会在很多地方被
SpringSecurity3.X--LDAP：AD配置 hanqunfeng SpringSecurity
前面介绍过基于本地数据库验证的方式，参考http://hanqunfeng.iteye.com/blog/1155226，这里说一下如何修改为使用AD进行身份验证【只对用户名和密码进行验证，权限依旧存储在本地数据库中】。将配置文件中的如下部分删除：
mac mysql 修改密码 IXHONG mysql
$ sudo /usr/local/mysql/bin/mysqld_safe –user=root & //启动MySQL(也可以通过偏好设置面板来启动)$ sudo /usr/local/mysql/bin/mysqladmin -uroot password yourpassword //设置MySQL密码（注意，这是第一次MySQL密码为空的时候的设置命令，如果是修改密码，还需在-
设计模式--抽象工厂模式 kerryg 设计模式
抽象工厂模式：工厂模式有一个问题就是，类的创建依赖于工厂类，也就是说，如果想要拓展程序，必须对工厂类进行修改，这违背了闭包原则。我们采用抽象工厂模式，创建多个工厂类，这样一旦需要增加新的功能，直接增加新的工厂类就可以了，不需要修改之前的代码。总结：这个模式的好处就是，如果想增加一个功能，就需要做一个实现类，
评"高中女生军训期跳楼” nannan408
首先，先抛出我的观点，各位看官少点砖头。那就是，中国的差异化教育必须做起来。孔圣人有云：有教无类。不同类型的人，都应该有对应的教育方法。目前中国的一体化教育，不知道已经扼杀了多少创造性人才。我们出不了爱迪生，出不了爱因斯坦，很大原因，是我们的培养思路错了，我们是第一要“顺从”。如果不顺从，我们的学校，就会用各种方法，罚站，罚写作业，各种罚。军
scala如何读取和写入文件内容？ qindongliang1922 java jvm scala
直接看如下代码： package file import java.io.RandomAccessFile import java.nio.charset.Charset import scala.io.Source import scala.reflect.io.{File, Path} /** * Created by qindongliang on 2015/
C语言算法之百元买百鸡 qiufeihu c 算法
中国古代数学家张丘建在他的《算经》中提出了一个著名的“百钱买百鸡问题”，鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一，百钱买百鸡，问翁，母，雏各几何？代码如下： #include <stdio.h> int main() { int cock,hen,chick; /*定义变量为基本整型*/ for(coc
Hadoop集群安全性：Hadoop中Namenode单点故障的解决方案及详细介绍AvatarNode wyz2009107220 NameNode
正如大家所知，NameNode在Hadoop系统中存在单点故障问题，这个对于标榜高可用性的Hadoop来说一直是个软肋。本文讨论一下为了解决这个问题而存在的几个solution。 1. Secondary NameNode 原理：Secondary NN会定期的从NN中读取editlog，与自己存储的Image进行合并形成新的metadata image 优点：Hadoop较早的版本都自带，