和 Nested Partition 有相通之处?
伯克利提出 AdaSearch:一种用于自适应搜索的逐步消除方法
在机器学习领域的诸多任务当中,我们通常希望能够立足预先给定的固定数据集找出问题的答案。然而,在某些应用场景下我们并没有先验数据可供参考 ; 相反,我们必须自行收集数据以回答那些自己感兴趣的问题。举例来说,这种情况在环境污染物监测以及人口普查类调查中就比较常见。自行收集数据的方式,使得我们能够将注意力集中在相关度最高的信息来源身上。然而,确定哪些信息来源能够生成有用的指标同样不是件易事。此外,当物理代理(例如机器人、卫星、人类等)进行数据收集时,我们必须首先规划需要测量的指标,以便缩短代理活动时长并降低相关成本。我们将这个抽象问题,称为自适应传感。
我们引入了一种新的方法以体现自适应感知问题,其中的机器人必须遍历所处环境以识别值得关注的位置或对象。自适应传感涵盖机器人技术当中众多已经得到充分研究的问题,包括快速识别意外污染泄漏与放射源,以及在搜索与救援任务当中寻找人类目标等。在这类场景当中,设计一条能够尽快返回正确解决方案的传感轨迹往往直接决定着任务的成败。
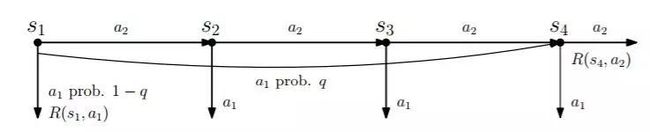
在这里,我们以放射源搜寻(简称 RSS)问题为例,其中无人机必须在所处环境中发现 K 个最为严重的发射性源头,而 K 为用户定义的参数。放射源搜寻属于自适应传感问题中一类特别有趣的例子,这主要是因为其中往往存在大量异质化明显的背景干扰,此外我们还很难找到适合统计置信区间且拥有良好表征的传感模型。
在这里我们引入了 AdaSearch,一套用于常规自适应传感问题的逐步消除框架,这里将在放射源搜寻场景下进行演示。AdaSearch 能够持续且明确地提供环境中每点放射率的置信区间。利用这些置信区间,算法将以迭代方式识别可能作为主要放射源的一组候选点,同时排除掉其它的点。
以体现搜索作为多重假设检验场景
从传统角度来讲,机器人社区一直将体现搜索(embodied search)目标设想为连续运动规划问题。其中,机器人必须在环境探索与有效轨迹选择之间做出有效平衡。这一基本思路意味着原有算法会将轨迹优化与探索结合至单一目标当中,从而利用滚动优化控制进行优化(参见 Hoffman 与 Tomlin、 Bai 等人、以及 Marchant 与 Ramos 的各自相关论文)。但我们的想法与此不同:我们希望建立起一种替代性方法,通过假设检验将问题表述为一种可排序的最佳行动识别。
在可排序的假设检验当中,我们的目标是通过迭代方式收集数据,从而针对多个单独问题得出结论。我们为代理提供一组 N 个测量行动,其中每种行动都根据不同的固定分布产生观察结果。
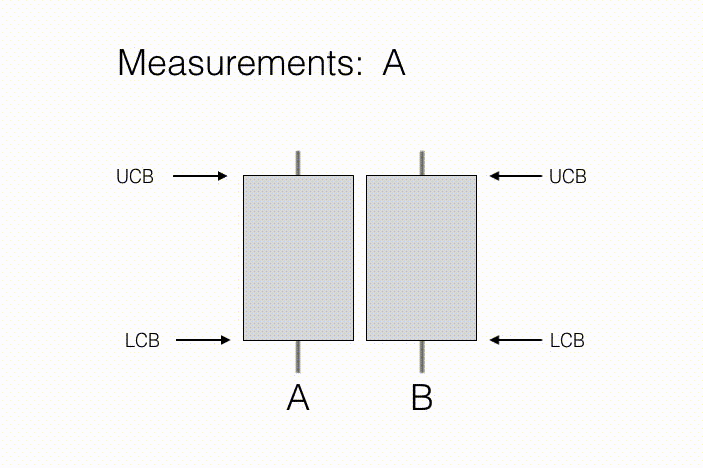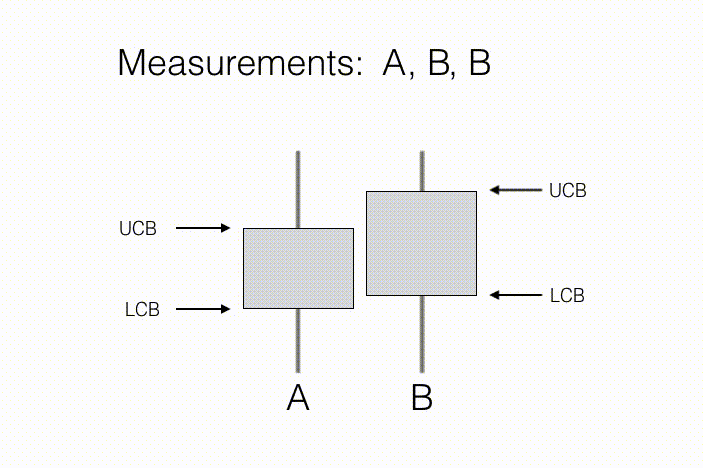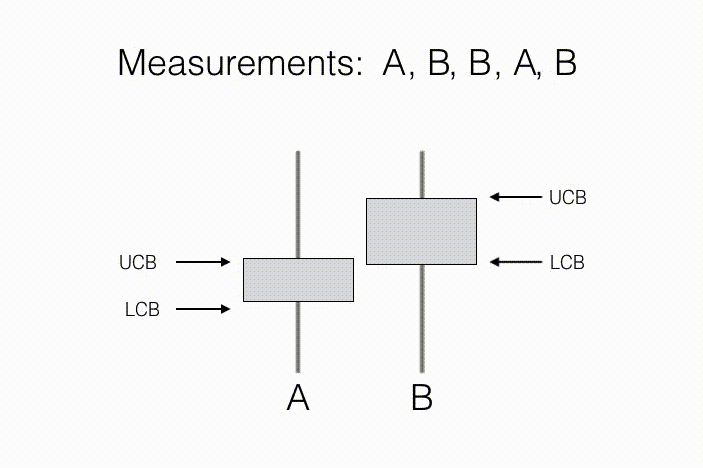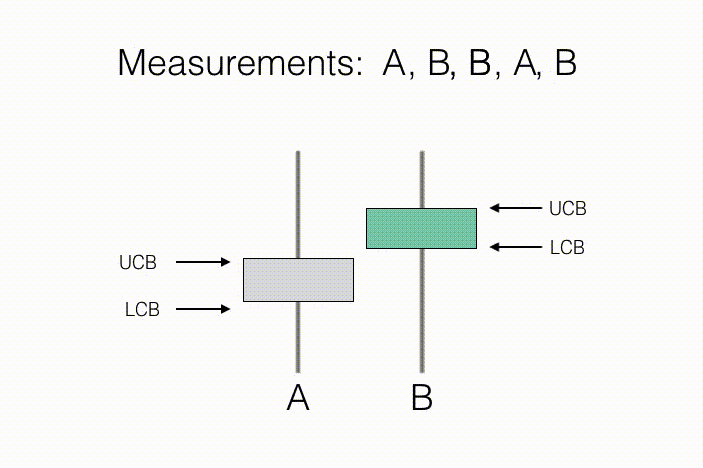
代理的目标是学习这些 N 个观测分布的一些预先指定的性质。举例来说,在“A/B 测试”这一统计问题当中,测量行动对应于向新客户展示产品 A 或产品 B,同时记录他们对于相关产品的评估意见。在这里,N=2,因为其中只涉及两种行动——向客户展示产品 A,以及向客户展示产品 B。其中需要关注的属性,在于哪款产品得到的平均反馈更好(如下图所示,B 的反馈更好)。随着收集到客户的偏爱情况,我们将能够获得产品样本平均反馈以及与之相关的置信区间,这一区间由每款产品的置信区间下限(简称 LCB)与置信区间上限(简称 UCB)予以描述。随着收集到的测量值不断增加,我们对于每款产品的反馈预估将更为自信,换言之我们能够进一步确定两款产品的真实排名。从结果来看,只要达成下述条件,则产品 B 的反馈要好于产品 A:如果产品 B 的置信下限高于产品 A 的置信上限,即可基本断定产品 B 的平均反馈情况有很大机率高于产品 A。
在环境感测场景下,每种行为都对应着一组来自给定位置与方向的传感器读数。通常来讲,代理希望了解哪项单一度量行为能够带来最大的平均观察信号值,或者说一组 K 项行为能够带来更高的总体平均观察值。为了实现这一目标,代理可能会利用以往观察到的结果按排序选择行为,从而尽可能采取具有最大平均观察值的行为以实现潜在的行动收益。
乍看起来,最佳行为排序识别这种方法似乎过于抽象了,很难在具体的移动传感代理当中发挥作用。但事实上,代理可以选择任意度量行为序列,而无需考虑潜在成本,例如与变更行为相关的活动时间。与此同时,最佳行动排序识别机制自身的抽象性质正是其最强大的力量所在。通过以精确的统计语言制定具体的搜寻问题,我们得以制定出与每项感测行为相关的可操作观察置信区间,同时在确定需要关注的目标观察点之前整理出所需采取的所有行为集合。
我们提出的具体搜寻方法正是 AdaSearch,其利用来自最佳行为排序识别与全局轨迹规划的启发式置信区间,从而分步渐近地实现复杂度最优度量,同时有效分摊活动成本。
放射源搜寻
为使阐述更加具体,我们将以单一放射源搜寻问题为场景解读 AdaSearch 的工作原理。我们将环境建模为一套平面网络,如下图所示。其中只存在一个高强度放射性源(下图中红点位置)。然而,定位该位置非常困难,因为传感器的测量功能会被背景辐射(即粉红点位置)所干扰。我们通过在网格上方部署配有辐射传感器的四旋翼飞行器来获取传感测量值。这一案例的目标,在于设计出一系列轨迹以确保机载传感器能够获得正确的测量值,从而使我们能够尽快将放射源位置与背景放射位置区分开来。
AdaSearch
我们的 AdaSearch 算法将全局覆盖规划方法与基于假设检验的自适应传感规则相结合,旨在定义出最优轨迹。在第一次进行网格探索时,我们会对整体环境进行均匀采样。
在经过第一轮探索与测量结果观察之后,我们可以略去其中一部分区域。如果某个点的置信区间上限低于其周边任何点的平均观察值置信区间下限,则将该点排除——这意味着其不太可能是我们需要搜寻的放射来源。
这个阈值对最终搜索结果最优的概率,这个影响是怎样的?
在下一轮搜寻中,AdaSearch 将专注于对作为潜在放射源位置的剩余点(即绿色方块)进行更细致地采样。
整个过程将不断继续,每轮的候选放射源数量也将持续减少,直到最终只剩下一个点。AdaSearch 会返回此点(即放大的红点),这就是搜寻工作最终给出的放射源答案。
由于整个统计公式清晰可信,因此我们基本可以肯定在已知的传感模型下,AdaSearch 有很高机率能够返回正确的放射源位置。我们在算法的整个执行过程当中设立固定的各单独区域周边置信界限宽度(以标准差方式),从而确保该概率具有一定程度的置信度。此外,AdaSearch 还提供特定于具体环境的运行时保证,更多详情请参考我们的论文。( https://arxiv.org/abs/1809.10611 )。
实验基准
对于常规自适应搜寻问题,目前最流行的解决方案当数信息最大化( Bourgault 等人提出)。信息最大化方法的基本思路在于根据信息理论标准在高机率位置收集测量值,并遵循滚动优化规划以进行轨迹规划。下面,我们将把 AdaSearch 与同样针对放射源搜寻场景定制的信息最大化方案 InfoMax 进行比较。
遗憾的是,对于规模较大的搜索区域,这种方法的实时计算存在诸多局限,例如只能给出规划范围与轨迹参数化的近似结果。这些近似结果可能导致算法贪婪性过高,且浪费太多时间以追踪无法解决问题的错误线索。
为了消除统计置信区间与全局规划启发(这一组合直接对打 InfoMax 中的信息指标与滚动优化规划)间的歧义,我们选择一种简单的全局规划方法 NaiveSearch 作为辅助基准。该方法会均匀地对网格进行采样,且保证在每个网格单元处花费相同的采样时间。
实验结果
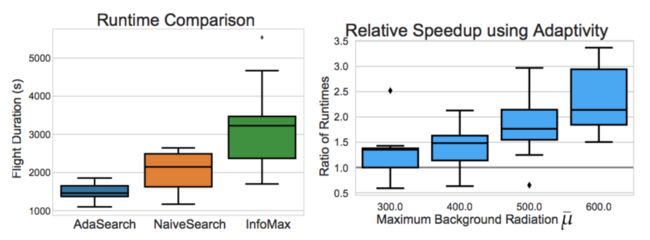
我们建立起全部三种算法,并立足一套以 4 米为基本网格单位的 64 x 64 环境下利用仿真四旋翼无人机加模拟辐射传感器读数对其进行了测试,希望了解三者在十种随机实例排布下的具体效能。
在我们的实验中,我们观察到 AdaSearch 在计算完成速度总体上快于 NaiveSearch 以及 InfoMax。随着我们不断增加背景辐射的最高水平,AdaSearch 相较于 NaiveSearch 的运行时间比较优势亦持续提升,这与论文中提出的理论界限相符。
AdaSearch 相较于 NaiveSearch 的效能提升表明,自适应性方法确实比非自适应方法更具优势。同样令人惊讶甚至出乎意料的是,即使是 NaiveSearch,在处理此类问题时也往往能够带来优于 InfoMax 的表现。这意味着 InfoMax 中采用的滚动优化控制方法存在局部贪婪性,并因此损害了其实际效能。相比之下,AdaSearch 则优雅地将自适应策略与全局覆盖保证加以结合。
AdaSearch 更具通用性
在放射源搜寻案例中大获得成功的无人机载 AdaSearch 演示,不禁令我们想到这种新型算法还能够在哪些更为常规 / 通用的问题中带来良好表现?事实证明,这种核心算法拥有相当广泛的适用范围,甚至适用于多种非机器人体现型传感问题。
举例来说,我们可以考虑在某一地区分布的 100 家医疗诊所中为 10 家规划试点计划的问题。我们可能需要立足诊所的具体位置进行调查,从而评估哪里才是某种特定罕见疾病发病率最高的区域或者各地区的具体发病率水平。这是一项具体型感测问题,因为诊断工作由医师亲自进行。很明显,人力调查员的数量有限,而且同一组调查员的工作时间需求以及在各诊所之间的往来成本都属于客观存在的物理限制。
调查工作的调度人员可以利用 AdaSearch 的指导意见整理各诊所位置在计算该疾病新病例时的具体用时,外加由此前往其它诊所的距离,从而权衡往来行程时长以确保调查人员能够在单位时间之内收集到更多相关数据。
一般来讲,当我们认为测量过程中的干扰因素足以保证算法在数据收集过程中完成多轮区域探索时,AdaSearch 即可带来良好的预期表现。无论是搜寻放射源头还是调查罕见疾病的发病率,我们都可以将其建模为泊松分布随机变量,其中的方差会随平均值变化而变化。AdaSearch 能够轻松适应不同的噪声模型(例如高斯模型),从而对接存在此类模型的多种不同应用场景。只要我们能够计算或者框定出适当的置信区间边界,AdaSearch 就能够保证有效遍历该区域以找到需要关注的目标点。
如果您希望了解关于 AdaSearch 的更多细节信息,可通过以下链接获取论文全文: https://arxiv.org/abs/1809.10611 。
查看原文链接:
https://bair.berkeley.edu/blog/2018/11/14/adasearch/
会议推荐:
12 月 20-21, AICon 全球人工智能与机器学习技术大会将于北京盛大开幕,学习来自 Google、微软、BAT、360、京东、美团等 40+AI 落地案例年终总结,与国内外一线技术大咖面对面交流,不见不散。
A Successive-Elimination Approach to Adaptive Robotic Source Seeking
We study an adaptive source seeking problem, in which a mobile robot must identify the strongest emitter(s) of a signal in an environment with background emissions. Background signals may be highly heterogeneous and can mislead algorithms that are based on receding horizon control, greedy heuristics, or smooth background priors. We propose AdaSearch, a general algorithm for adaptive source seeking in the face of heterogeneous background noise. AdaSearch combines global trajectory planning with principled confidence intervals in order to concentrate measurements in promising regions while guaranteeing sufficient coverage of the entire area. Theoretical analysis shows that AdaSearch confers gains over a uniform sampling strategy when the distribution of background signals is highly variable. Simulation experiments demonstrate that when applied to the problem of radioactive source seeking, AdaSearch outperforms both uniform sampling and a receding time horizon information-maximization approach based on the current literature. We also demonstrate AdaSearch in hardware, providing further evidence of its potential for real-time implementation.
谷歌发布 TensorFlow Serving 开源项目:更快的将深度学习模型产品商业化
阅读数:42272016 年 2 月 19 日 18:00
机器学习现在变得越来越流行了,不仅被大力应用于像 Google 和 Facebook 这样的网络公司,也被普遍应用到大量的创业公司当中。
机器学习经过几十年软件工业的实践已达到产品级别,现已应用在 Google 各系列产品中, 从 Google app 中的语音识别,Google Mail 中的自动回复到 Google Photo 的搜索。但要把这些机器学习模型做成服务对外提供使用是一种新的挑战。
TensorFlow 开源之后,今天 Google 又宣布发布面向生产环境的 TensorFlow Serving,旨在解决上述挑战。Google 软件工程师 Noah Fiedel 在博文中介绍,“TensorFlow Serving 是一个高性能、开源的机器学习服务系统,为生产环境及优化 TensorFlow 而设计。它更适合运行多个大规模模型,并支持模型生命周期管理、多种算法实验及有效地利用 GPU 资源。TensorFlow Serving 能够让训练好的模型更快、更易于投入生产环境使用。
这里有必要先科普下 TensorFlow 和 TensorFlow Serving 的区别:
TensorFlow 项目主要是基于各种机器学习算法构建模型,并为某些特定类型的数据输入做适应学习,而 TensorFlow Serving 则专注于让这些模型能够加入到产品环境中。开发者使用 TensorFlow 构建模型,然后 TensorFlow Serving 基于客户端输入的数据使用前面 TensorFlow 训练好的模型进行预测。
个人认为 TensorFlow Serving 是将 tensorflow 训练出来的模型更好的应用于生产环境中,通过它的 API 等支持的方式来方便对外提供稳定可靠的服务。TensorFlow Serving 的意义就在于能够很方便的将深度学习生产化,解决了模型无法提供服务的弊端,并且用的是 c++ 语言,性能上应该不错。这样以后深度学习方向的创业公司都能很方便的将产品商业化,保证 7*24 小时的可靠服务。
如谷哥所说,TensorFlow Serving 可以在不改变现有模型架构和 API 的基础上发布新的模型和实验数据到产品中。它不仅仅支持 TensorFlow 训练的模型,也可以扩展到其他类型的模型 (比如 Scikit Learn 生成的模型)。
下面讲下 TensorFlow Serving 使用的具体例子:
给个简单的监督学习的训练 pipeline,如图 1
图 1
在图 1 中,输入训练数据 (Data) 到学习者 (Learner) 中,输出训练成功的模型 (Model 1)。
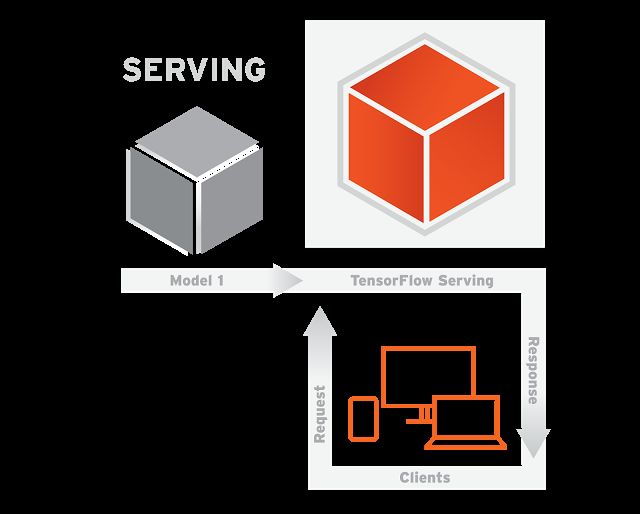
一旦新版本的模型训练好就可以发布到服务系统 (TensorFlow Serving) 上,如图 2
图 2
在图 2 中,TensorFlow Serving 利用上面训练好的模型基于客户端 (Clients) 提供的数据进行预测结果。这里客户端和服务端之间的通信采用的是 RPC 协议 (Google 开源的一个高性能 RPC 的实现,gRPC 源代码见 http://www.grpc.io )。
对于生产环境来说,启动模型,随着时间不断迭代模型,新的训练数据出现需要训练优化模型,这些都是常态。现在有了 TensorFlow Serving 就可以在不停止服务的情况下更新模型和数据,Google 内部许多 pipelines 一直在运行。
TensorFlow Serving 采用 C++ 编写,支持 Linux。为性能做有优化,在 16 核至强 CPU 设备上,每核每秒能够处理超过 10 万个请求,这里包括 gRPC 和 TensorFlow 接口之间的处理时间。 TensorFlow Serving 代码和教程已经能够在GitHub 获取。
TensorFlow 官方简化版!谷歌开源机器学习库 JAX
- 陈思
阅读数:15212018 年 12 月 12 日 07:00
AI 前线导读:什么?TensorFlow 有了替代品?什么?竟然还是谷歌自己做出来的?先别慌,从各种意义上来说,这个所谓的“替代品”其实是 TensorFlow 的一个简化库,名为 JAX,结合 Autograd 和 XLA,可以支持部分 TensorFlow 的功能,但是比 TensorFlow 更加简洁易用。虽然还不至于替代 TensorFlow,但已经有 Reddit 网友对 JAX 寄予厚望,并表示“早就期待能有一个可以直接调用 Numpy API 接口的库了!”,“希望它可以取代 TensorFlow!”。
更多干货内容请关注微信公众号“AI 前线”(ID:ai-front)
JAX 结合了 Autograd 和 XLA,是专为高性能机器学习研究打造的产品。
有了新版本的 Autograd,JAX 能够自动对 Python 和 NumPy 的自带函数求导,支持循环、分支、递归、闭包函数求导,而且可以求三阶导数。它支持自动模式反向求导(也就是反向传播)和正向求导,且二者可以任意组合成任何顺序。
JAX 的创新之处在于,它基于 XLA 在 GPU 和 TPU 上编译和运行 NumPy 程序。默认情况下,编译是在底层进行的,库调用能够及时编译和执行。但是 JAX 还允许使用单一函数 API jit将自己的 Python 函数及时编译成经过 XLA 优化的内核。编译和自动求导可以任意组合,因此可以在不脱离 Python 环境的情况下实现复杂算法并获得最优性能。
JAX 最初由 Matt Johnson、Roy Frostig、Dougal Maclaurin 和 Chris Leary 发起,他们均任职于谷歌大脑团队。在 GitHub 的说明文档中,作者明确表示:JAX 目前还只是一个研究项目,不是谷歌的官方产品,因此可能会有一些 bug。从作者的 GitHub 简介来看,这应该是谷歌大脑正在尝试的新项目,在同一个 GitHub 目录下的开源项目还包括 8 月份在业内引起热议的强化学习框架 Dopamine。
以下是 JAX 的简单使用示例。
GitHub 项目传送门: https://github.com/google/JAX
有关具体的安装和简单的入门指导大家可以在 GitHub 中自行查看,在此不做过多赘述。
JAX 库的实现原理
机器学习中的编程是关于函数的表达和转换。转换包括自动微分、加速器编译和自动批处理。像 Python 这样的高级语言非常适合表达函数,但是通常使用者只能应用它们。我们无法访问它们的内部结构,因此无法执行转换。
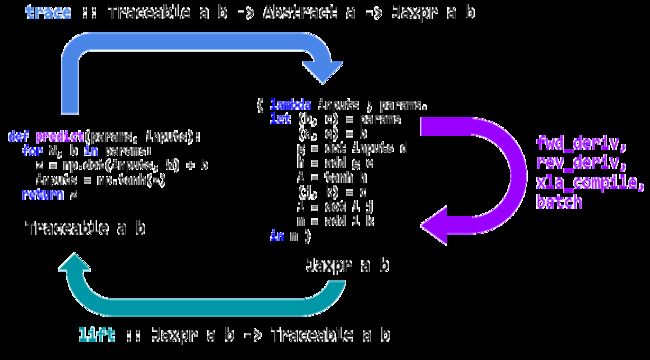
JAX 可以用于专门化高级 Python+NumPy 函数,并将其转换为可转换的表示形式,然后再提升为 Python 函数。
JAX 通过跟踪专门处理 Python 函数。跟踪一个函数意味着:监视应用于其输入,以产生其输出的所有基本操作,并在有向无环图 (DAG) 中记录这些操作及其之间的数据流。为了执行跟踪,JAX 包装了基本的操作,就像基本的数字内核一样,这样一来,当调用它们时,它们就会将自己添加到执行的操作列表以及输入和输出中。为了跟踪这些原语之间的数据流,跟踪的值被包装在 Tracer 类的实例中。
当 Python 函数被提供给 grad 或 jit 时,它被包装起来以便跟踪并返回。当调用包装的函数时,我们将提供的具体参数抽象到 AbstractValue 类的实例中,将它们框起来用于跟踪跟踪器类的实例,并对它们调用函数。
抽象参数表示一组可能的值,而不是特定的值:例如,jit 将 ndarray 参数抽象为抽象值,这些值表示具有相同形状和数据类型的所有 ndarray。相反,grad 抽象 ndarray 参数来表示底层值的无穷小邻域。通过在这些抽象值上跟踪 Python 函数,我们确保它足够专门化,以便转换是可处理的,并且它仍然足够通用,以便转换后的结果是有用的,并且可能是可重用的。然后将这些转换后的函数提升回 Python 可调用函数,这样就可以根据需要跟踪并再次转换它们。
JAX 跟踪的基本函数大多与 XLA HLO 1:1 对应,并在 lax.py 中定义。这种 1:1 的对应关系使得到 XLA 的大多数转换基本上都很简单,并且确保我们只有一小组原语来覆盖其他转换,比如自动微分。 jax.numpy 层是用纯 Python 编写的,它只是用 LAX 函数 (以及我们已经编写的其他 numpy 函数) 表示 numpy 函数。这使得 jax.numpy 易于延展。
当你使用 jax.numpy 时,底层 LAX 原语是在后台进行 jit 编译的,允许你在加速器上执行每个原语操作的同时编写不受限制的 Python+ numpy 代码。
但是 JAX 可以做更多的事情:你可以在越来越大的函数上使用 jit 来进行端到端编译和优化,而不仅仅是编译和调度到一组固定的单个原语。例如,可以编译整个网络,或者编译整个梯度计算和优化器更新步骤,而不仅仅是编译和调度卷积运算。
折衷之处是,jit 函数必须满足一些额外的专门化需求:因为我们希望编译专门针对形状和数据类型的跟踪,但不是专门针对具体值的跟踪,所以 jit 装饰器下的 Python 代码必须适用于抽象值。如果我们尝试在一个抽象的 x 上求 x >0 的值,结果是一个抽象的值,表示集合{True, False},所以 Python 分支就像 if x > 0 会引起报错。
有关使用 jit 的更多要求,请参见: https://github.com/google/jax#whats-supported
好消息是,jit 是可选的:JAX 库在后台对单个操作和函数使用 jit,允许编写不受限制的 Python+Numpy,同时仍然使用硬件加速器。但是,当你希望最大化性能时,通常可以在自己的代码中使用 jit 编译和端到端优化更大的函数。
后续计划
目前项目小组还将对以下几项做更多尝试和更新:
-
完善说明文档
-
支持 Cloud TPU
-
支持多 GPU 和多 TPU
-
支持完整的 NumPy 功能和部分 SciPy 功能
-
全面支持 vmap
-
加速
- 降低 XLA 函数调度开销
- 线性代数例程(CPU 上的 MKL 和 GPU 上的 MAGMA)
-
高效自动微分原语
cond和while
有关 JAX 库的介绍大致如此,如果你在尝试了 JAX 之后有一些较好的使用心得,欢迎随时向我们投稿,AI 前线十分愿意将你的经验传播给更多开发者。
再次附上 GitHub 链接: https://github.com/google/jax
相关资源:
JAX 论文链接: https://www.sysml.cc/doc/146.pdf
【读书笔记】NeurIPS2018的两篇文章:The Tradeoffs of Large Scale Learning和Neural Ordinary Differential Equations
今天看了 NeurIPS 2018 上的两篇文章,一篇是获得 best paper 的 Neural Ordinary Differential Equations (陈天奇的文章),一篇是获经典论文奖的 The Tradeoffs of Large Scale Learning。
The Tradeoffs of Large Scale Learning
Bottou, Léon, and Olivier Bousquet. “The tradeoffs of large scale learning.” Advances in neural information processing systems. 2008.
Abstract
本文研究不同的近似优化算法对学习算法的影响。Small-scale learning problems 受到 approximation–estimation 的影响,Large-scale learning problems 受到优化算法计算复杂度的影响。
Motivation
计算复杂度在学习算法中的有重要的意义,但很少被提及。Valiant 强调一个问题是可学习的,如果一个算法能在多项式复杂度内解决它。但是这只是在统计意义上的解决。
本文发现近似优化算法完全可以满足学习要求,而且降低计算复杂度。
Approximate Optimization
Setup
优化算法优化的对象是
E(f)=∫l(f(x),y)dP(x,y)=E[l(f(x),y)]
也就是要求解
f∗=argminfE[l(y^,y)∣x]
尽管P(x,y)未知,我们可以随机独立采样得到n个数据来做训练数据,定义经验误差
En(f)=n1i=1∑nl(f(xi),yi)=En[l(f(xi),yi)]
我们的学习过程实际上是根据训练数据从一组函数F内选择出函数fn=argminfEn[f],定义f∗为所有可能的最优的函数(可能不在F中),在定义fF∗=argminfE[f]为F中最优的函数,那么我们有:
E[E(fn)−E(f∗]]=E[E(fF∗)−E(f∗)]+E[E(fn)−E(fF∗)]=eapp+eest
eapp表示 approximation error(F与最优解的差距),eest表示 estimation error(由于训练数据和优化算法得到的函数与F内最优函数的差距)。复杂的模型导致大的F,大的F导致小的 approximation error 而导致大的 estimation error。
Optimization Error
找到最优的fn需要很复杂的计算,而我们不需要找到最优的fn,因为En(f)本身就是近似的,所以我们可以在优化算法收敛前提前终止迭代。
假设我们得到的近似解为f^n满足
En(f^n)
ρ是预先定义的 tolerance,那么
E[E(f^n)−E(f∗]]=E[E(fF∗)−E(f∗)]+E[E(fn)−E(fF∗)]+E[E(f^n)−E(fn)]=eapp+eest+eopt
就多出一个 optimization error eopt。
The Approximation–Estimation–Optimization Tradeoff
对于整个问题而言,我们需要优化的是
minF,ρ,ne=eapp+eest+eopt,s.t.n≤nmax,T(F,ρ,n)≤Tmax
nmax表示最大的可用数据量,Tmax表示能够训练的最长时间。
所谓 Small-scale learning problems 是指主要收到nmax的限制,计算复杂度不成问题,eopt可以减少为0;而 Large-scale learning problem 主要受到Tmax的限制,我们需要选择合适ρ来简化计算。
 GD:梯度下降法
GD:梯度下降法
2GD:二阶梯度下降法(牛顿法)
SGD:随机梯度下降法
2SGD:二阶随机梯度下降法
The Asymptotics of Large-scale Learning
涉及到优化算法的收敛速度的相关理论知识
Conclusion
本文主要思想是考虑数据量较大时对于时间的权衡,我的理解是从理论上给予了随机梯度下降和梯度下降选择的依据。
Neural Ordinary Differential Equations
Chen, Tian Qi, et al. “Neural Ordinary Differential Equations.” arXiv preprint arXiv:1806.07366 (2018).
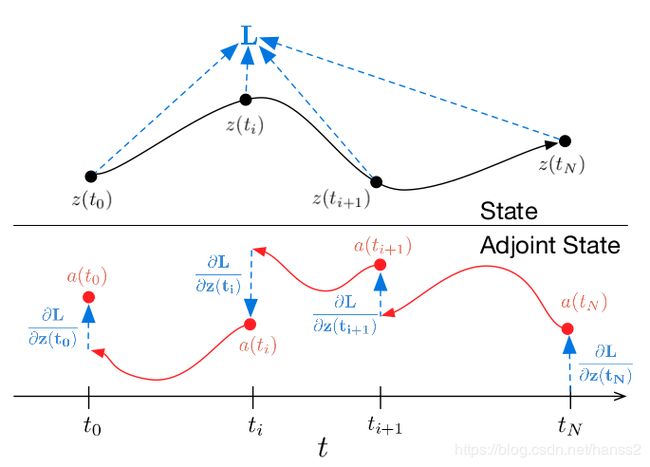
引入了一种新型的神经网络,区别于过去的多个离散层的神经网络,我们的神经网络时各黑箱的微分方程的求解器。这种连续深度的神经网络优势是只需要花费恒定的内存,并且可以显式地以数值精度换取速度。构建 continuous normalizing flows 从而可以通过最大似然进行训练、无需对数据维度进行分区或排序。对于训练,我们展示了如何在不访问任何ODE求解器内部操作的情况下,可扩展地反向传播。这允许在更大的模型中对ODE进行端到端训练。
思路是常规的 ResNet 相当于
ht+1=ht+f(ht,θt)
可以看作是一个微分方程的 Euler 迭代求解。如果用更多的层数和更小的步长,可以化为
dtdh=f(h(t),t,θ)
根据流体力学的一些结论,推导出了微分方程的解法,细节没有仔细看,逛了逛知乎,发现 https://zhuanlan.zhihu.com/p/51514687 上有人也有类似的想法,并且也有一些列的工作,感觉挺有趣的。主要思想是把常规的离散形式的神经网络转化为 ODE 进行训练和分析:
- ResNet- ODE的前向欧拉格式
- PolyNet- ODE的反向欧拉格式的逼近
- FractalNet-ODE的Runge-Kutta 格式
感觉跟跟我的老本行有点像,有空好好研究一下。
【论文夜读】陈天琦神作Neural Ordinary Differential Equations(NuerIPS2018最佳paper)
在最近结束的 NeruIPS 2018 中,来自多伦多大学的陈天琦等研究者成为最佳论文的获得者。在与机器之心的访谈中,陈天琦的导师 David Duvenaud 教授谈起这位学生也是赞不绝口。Duvenaud 教授认为陈天琦不仅是位理解能力超强的学生,钻研起问题来也相当认真透彻。他说:「天琦很喜欢提出新想法,他有时会在我提出建议一周后再反馈:『老师你之前建议的方法不太合理。但是我研究出另外一套合理的方法,结果我也做出来了。』」Ducenaud 教授评价道,现如今人工智能热度有增无减,教授能找到优秀博士生基本如同「鸡生蛋还是蛋生鸡」的问题,顶尖学校的教授通常能快速地招纳到博士生,「我很幸运地能在事业起步阶段就遇到陈天琦如此优秀的学生。」
本文的精粹
最近慢慢涌现了一些对该文的解读,而我主要从定理推导的角度谈谈这篇文章的一些精粹:比如文中关于一个导数计算的变量变元定理(它将一个不太容易计算的梯度∂t∂logp(t)转化为了好计算的梯度−tr(dzdf(t)));
本文的核心内容复习
在这里过一下这篇论文说了啥:大概就是根据常微分方程ODE的启发引入了一种新型的神经网络ODE Net,区别于过去的多个离散层的神经网(文中用ResNet作对比).总体来说是一篇比较偏理论,逻辑完善推导严密的论文;
常规的 ResNet 的层迭代相当于:ht+1=ht+f(ht,θt);
这等价于一个微分方程的 Euler 迭代求解,如果用更多的层数和但更小的步长,可以优化为:
dtdh(t)=f(h(t),t,θ)
这里就是论文的全部核心idea了,剩下的问题是如何用于网络训练.对于训练,作者展示了如何在不涉及任何特殊ODE求解器内部操作的情况下(意思是所有的微分方程采样一种通用的办法求解),可扩展地反向传播.这允许在更大的模型中对ODE进行端到端训练.
梯度变元定理
- 定理:Let x(t) be a finite continuous random variable with probability p(x(t))dependent on time.Let dtdx=f(x(t),t) be a differential equation describing a continuous-in-time transformation of x(t).Assuming that f is uniformly Lipschitz continuous in x and continuous in t, then the change in log probability also follows a differential equation(这是一堆众所周知的前提条件,可以跳过):
∂t∂logp(z(t))=−tr(dzdf(t))
这里讲讲证明的核心思想,首先,将ϵ时长后的z值表达为:z(t+ϵ)=Tϵ(z(t)),然后容易推导出:
∂t∂logp(z(t))=−tr(ϵ→0+lim∂ϵ∂∂z∂Tϵ(z(t)))
然后对Tϵ(z(t))作泰勒展开即可:
∂t∂logp(z(t))=−tr(ϵ→0+lim∂ϵ∂∂z∂(z+ϵf(z(t),t)+O(ϵ2)+O(ϵ3)+…))
=−tr(ϵ→0+lim∂ϵ∂(I+∂z∂ϵf(z(t),t)+O(ϵ2)+O(ϵ3)+…))
=−tr(ϵ→0+lim(∂z∂f(z(t),t)+O(ϵ)+O(ϵ2)+…))
=−tr(∂z∂f(z(t),t))
一点八卦
但是我们隐约感觉修过ODE的工科生貌似不难想到这个idea,果然,有人称,这个idea是之前有人想到的:
知乎上一个人之前的idea
知乎上一个人的看法
谁是谁非,大家自己判断吧;
NeurIPS 2018最佳论文出炉:UT陈天琦、华为上榜
经历了改名、抢票和论文评审等等风波的「预热」,第 32 届 NeurIPS 于当地时间 12 月 3 日在加拿大蒙特利尔正式开幕。机器之心有幸参与了「第一届 NeurIPS」。
在大会第一天的 Opening Remarks 上,NeurIPS 2018 公布了本届大会的获奖论文。来自多伦多大学的陈天琦、麦克马斯特大学的 Hassan Ashtiani、谷歌 AI 的 Tyler Lu,以及华为诺亚方舟实验室的 Kevin Scaman 等人成为了最佳论文奖的获得者。
作为人工智能的顶级会议,NeurIPS 究竟有多火?首先,让我们看看参会人数的变化:2016 年有 5000 人注册参加该会议,2017 年参会人数飙升至 8000,今年参会人数近 9000,且出现了 11 分钟大会门票被抢光的盛况,仅次于 Beyonce 音乐会的售票速度。
在活动方面,今年新增了 Expo 环节,吸引了全球 32 家公司的参与。在 12 月 2 日的 Expo 中,这些公司共组织了 15 场 Talk&Pannel、17 场 Demonstration、10 场 workshop。此外,为期一周的整个大会包含 4 个 tutorial session、5 场 invited talk、39 场 workshop 等。
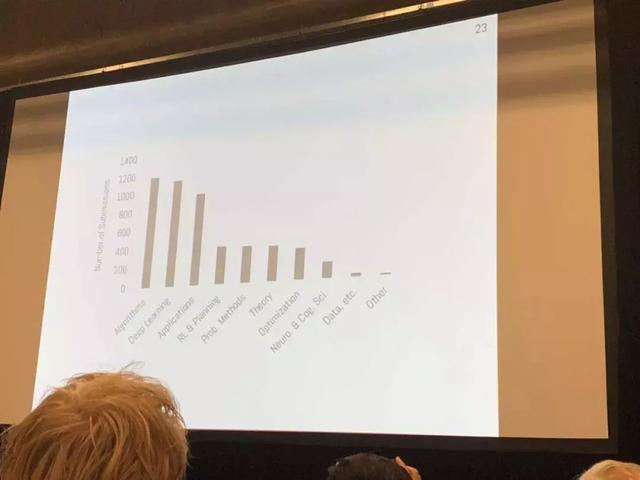
至于论文方面,NeurIPS 2018 共收到 4856 篇投稿,创历史最高记录,最终录取了 1011 篇论文,其中 Spotlight 168 篇 (3.5%),oral 论文 30 篇 (0.6%)。
而这些论文涉及的主题包括算法、深度学习、应用、强化学习与规划等。大会程序委员联合主席表示,这些提交论文中,69% 的论文作者表示将放出代码(结果只有 44%),42% 将公布数据。
介绍完大会基本信息,我们来看看今年的最佳论文:
4 篇最佳论文(Best paper awards)
论文:Neural Ordinary Differential Equations
- 作者:Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud(四人均来自多伦多大学向量研究所)
- 链接:https://papers.nips.cc/paper/7892-neural-ordinary-differential-equations.pdf
摘要:本研究介绍了一种新的深度神经网络模型家族。我们并没有规定一个离散的隐藏层序列,而是使用神经网络将隐藏状态的导数参数化。然后使用黑箱微分方程求解器计算该网络的输出。这些连续深度模型(continuous-depth model)的内存成本是固定的,它们根据输入调整评估策略,并显式地用数值精度来换取运算速度。我们展示了连续深度残差网络和连续时间隐变量模型的特性。此外,我们还构建了连续的归一化流,即一个可以使用最大似然训练的生成模型,无需对数据维度进行分割或排序。至于训练,我们展示了如何基于任意 ODE 求解器进行可扩展的反向传播,无需访问 ODE 求解器的内部操作。这使得在较大模型内也可以实现 ODE 的端到端训练。
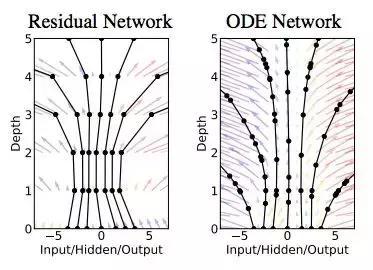
图 1:左:残差网络定义离散序列的有限变换。右:ODE 网络定义向量场,其连续变换状态。两张图中的黑色圆圈表示评估位置(evaluation location)。
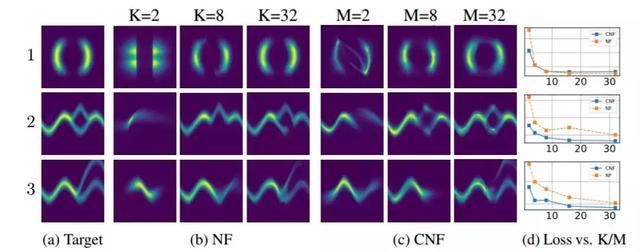
图 4:归一化流和连续归一化流的对比。归一化流的模型容量由深度(K)决定,而连续归一化流可以通过增加宽度(M)来增加模型容量,这使其更加容易训练。
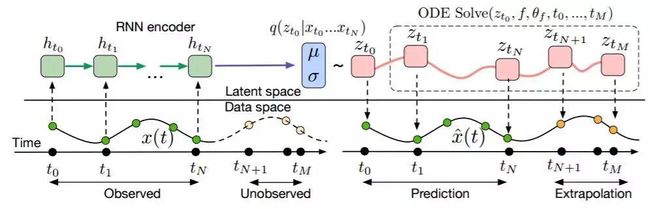
图 6:隐 ODE 模型的计算图。
论文:Nearly tight sample complexity bounds for learning mixtures of Gaussians via sample compression schemes
- 作者:Hassan Ashtiani、Shai Ben-David 等(麦克马斯特大学、滑铁卢大学等)
- 链接:https://papers.nips.cc/paper/7601-nearly-tight-sample-complexity-bounds-for-learning-mixtures-of-gaussians-via-sample-compression-schemes.pdf
本文作者证明了
![]()
样本对于学习 R^d 中 k-高斯混合模型是必要及充分的,总变分距离的误差为ε。这一研究改善了该问题的已知上限和下限。对于轴对齐高斯混合模型,本文表明
样本是充分的,与已知的下限相匹配。其上限的证明基于一种基于样本压缩概念的分布学习新技术。任何允许这种样本压缩方案的类别分布也可以用很少的样本来学习。此外,如果一类分布有这样的压缩方案,那么这些分布的乘积和混合也是如此。本研究的核心结果是证明了 R^d 中的高斯类别具有有效的样本压缩。
论文:Non-delusional Q-learning and value-iteration
- 作者:Tyler Lu(Google AI)、Dale Schuurmans(Google AI)、Craig Boutilier(Google AI)
- 链接:https://papers.nips.cc/paper/8200-non-delusional-q-learning-and-value-iteration.pdf
摘要:本研究发现了使用函数近似的 Q-learning 和其它形式的动态规划中的一个基本误差源。当近似架构限制了可表达贪婪策略的类别时,就会产生 delusional bias。由于标准 Q 更新对于可表达的策略类作出了全局不协调的动作选择,因此会导致不一致甚至冲突的 Q 值估计,进而导致高估/低估、不稳定、发散等病态行为。为了解决这个问题,作者引入了一种新的策略一致性概念,并定义了一个本地备份过程,该过程通过使用信息集(这些信息记录了与备份 Q 值一致的策略约束)来确保全局一致性。本文证明,基于模型和无模型的算法都可以利用这种备份消除 delusional bias,并产生了第一批能够保证一般情况下最佳结果的已知算法。此外,这些算法只需要多项式的信息集(源于潜在的指数支持)。最后,作者建议了其它尝试消除 delusional bias 的实用价值迭代和 Q-learning 的启发式方法。
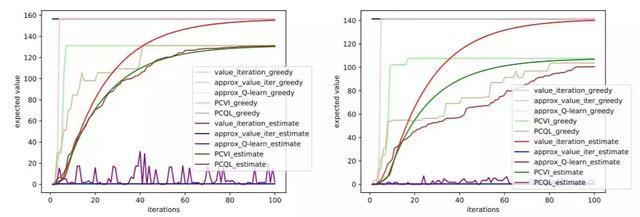
图 1:一个简单的 MDP,展示了 delusional bias。
图 2:在一个具有随机特征表征的网格世界中进行规划及学习。图中的「iterations」是指遍历状态-动作对,Q-learning 和 PCQL 除外。深色线:估计可达到的最大期望值。浅色线:贪婪策略所达到的实际期望值。
论文:Optimal Algorithms for Non-Smooth Distributed Optimization in Networks
- 作者:Kevin Scaman(华为诺亚方舟实验室)、Francis Bach(PSL 研究大学)、Sébastien Bubeck(微软研究院)、Yin Tat Lee(微软研究院)、Laurent Massoulié(PSL 研究大学)
- 链接:https://papers.nips.cc/paper/7539-optimal-algorithms-for-non-smooth-distributed-optimization-in-networks.pdf
摘要:本研究考虑使用计算单元网络对非光滑凸函数进行分布式优化。我们在两种规则假设下研究该问题:1)全局目标函数的利普希茨连续;2)局部单个函数的利普希茨连续。在局部假设下,我们得到了最优一阶分散式算法(decentralized algorithm)——多步原始对偶(multi-step primal-dual,MSPD)及其对应的最优收敛速率。该结果重要的方面在于,对于非光滑函数,尽管误差的主要项在 O(1/ sqrt(t)) 中,但通讯网络(communication network)的结构仅影响 O(1/t) 中的二阶项(t 是时间)。也就是说,通讯资源限制导致的误差会以非常快的速度降低,即使是在非强凸目标函数中。在全局假设下,我们得到了一个简单但高效的算法——分布式随机平滑(distributed randomized smoothing,DRS)算法,它基于目标函数的局部平滑。研究证明 DRS 的最优收敛速率在 d^(1/4) 乘积因子内(d 是潜在维度)。
经典论文奖(Test of time award)
去年的经典论文颁给了核函数加速训练方法,今年的经典论文也是一篇偏理论的研究论文,它们都是 2007 年的研究。
论文:The Tradeoffs of Large Scale Learning
- 作者:Le´on Bottou(NEC laboratories of America)、Olivier Bousquet(谷歌)
- 链接:https://papers.nips.cc/paper/3323-the-tradeoffs-of-large-scale-learning.pdf
该论文的贡献在于开发了一个理论框架,其考虑了近似优化对学习算法的影响。该分析展示了小规模学习和大规模学习的显著权衡问题。小规模学习受到一般近似估计权衡的影响,而大规模学习问题通常要在质上进行不同的折中,且这种权衡涉及潜在优化算法的计算复杂度,它基本上是不可求解的。
表 2:梯度下降算法的渐进结果,倒数第二列为到达准确率的优化时间,最后一列为到达超过测试误差率 epsilon 的优化时间。其中 d 为参数维度、n 为样本数。
作为本次大会的受邀媒体,机器之心来到了蒙特利尔,参与了本次 NeruIPS 大会。未来几天,我们还将发来最新现场报道,敬请期待。
机器之心NeurIPS 2018 论文报道系列:
- NeurIPS 2018相关论文链接:
- NeurIPS 2018提前看:生物学与学习算法
- NeurIPS 2018,最佳论文也许就藏在这30篇oral论文中
- NeurIPS 2018 | 腾讯AI Lab&北大提出基于随机路径积分的差分估计子非凸优化
- NeurIPS 2018亮点选读:深度推理学习中的图网络与关系表征
- NeurIPS 2018提前看:可视化神经网络泛化能力
- Google AI提出物体识别新方法:端到端发现同类物体最优3D关键点——NeurIPS 2018提前看
- MIT等提出NS-VQA:结合深度学习与符号推理的视觉问答
- 画个草图生成2K高清视频,这份效果惊艳研究值得你跑一跑
- 下一个GAN?OpenAI提出可逆生成模型Glow
- CMU、NYU与FAIR共同提出GLoMo:迁移学习新范式
- Quoc Le提出卷积网络专属正则化方法DropBlock
- Edward2.2,一种可以用TPU大规模训练的概率编程
- 南大周志华等人提出无组织恶意攻击检测算法UMA
- MIT新研究参透批归一化原理
- 程序翻译新突破:UC伯克利提出树到树的程序翻译神经网络
- 将RNN内存占用缩小90%:多伦多大学提出可逆循环神经网络
- 哪种特征分析法适合你的任务?Ian Goodfellow提出显著性映射的可用性测试
- 行人重识别告别辅助姿势信息,商汤、中科大提出姿势无关的特征提取GAN
- 作为多目标优化的多任务学习:寻找帕累托最优解
- Dropout可能要换了,Hinton等研究者提出神似剪枝的Targeted Dropout
- 利用Capsule重构过程,Hinton等人实现对抗样本的自动检测
大规模学习该如何权衡得失?解读 NeurIPS 2018 时间检验奖获奖论文
- 姚佳灵
阅读数:6622018 年 12 月 16 日 14:00
AI 前线导读:机器学习进展飞速,有时甚至觉得,超过 2 年的想法或算法就过时了,或者就被其他更好的东西所取代。然而有时候,有些旧想法,即使科学界的大部分人已经远离它们,它们仍然很重要。这通常是个上下文的问题:一个在特定的上下文中看起来已经穷途末路的想法也许在另一个上下文中变得极其成功。在深度学习的特定情况下,可用数据和计算能力的增长重新引起了人们对该领域的兴趣,并显著地影响了研究方向。
更多干货内容请关注微信公众号“AI 前线”(ID:ai-front)
NIPS 2007 年的论文 《大规模学习的权衡(The Trade-Off of Large Scale Learning)》 是由 Léon Bottou(当时在 NEC 实验室 工作,现在在 Facebook AI 研究中心 工作)和 Olivier Bousquet(就职于 苏黎世谷歌 AI 研究中心 )共同完成的,该论文是这种现象的绝佳实例。作为 NeurIPS 2018 经典论文奖的获奖论文,这项开创性的工作研究了机器学习中的数据和计算之间的相互作用。研究结果显示,即使受到计算能力的限制,仍然可以使用大型数据集,在多个独立训练样本上进行少量的计算比在数据的子集上进行大量的计算更有效率。这证明了 随机梯度下降法 这个旧算法的强大,如今,几乎所有的深度学习应用都使用了该算法。本文是 AI 前线第 62 篇论文导读,我们将带大家一起回顾这篇经典论文。
优化和扩展挑战
很多机器学习算法都可以看成是以下两个要素的组合:
-
模型:一个可以用于拟合数据的函数集合。
-
优化算法:指明如何在该函数集合中找到最佳函数。
回望 90 年代,机器学习中使用的数据集比如今使用的要小很多,尽管人工神经网络已经取得一些成功,但它们仍然被认为难以训练。在 2000 年初,随着“核机器(Kernel Machines )”(特别是 SVM )的引入,神经网络逐渐落伍。同时,大家的注意力从一直用于训练神经网络的优化算法(随机梯度下降法)转移到了用于核机器的那些算法上(quadratic programming,二次规划)。一个重要的区别是,在前一种情况下,一次使用一个训练样本执行梯度步骤(这被称为“随机”),而在后一种情况下,每次迭代时都会用到所有训练样本(这被称为“批处理”)。
随着训练集规模的增长,优化算法处理大量数据的效率成为瓶颈。比如,在二次规划的情况下,运行时间至少是样本数量的二次方。换句话说,如果训练集的规模翻倍,那么训练时间至少要增加 4 倍。因此,为了把这些算法扩展到更大的训练集,人们花费了大量的精力(请参看 大规模核机器 )。
具有神经网络训练经验的人都知道,随机梯度下降法相对更容易扩展到大型数据集,但是,遗憾的是,它的收敛速度非常慢(要进行大量迭代才能达到与批处理算法的精度),因此,还不清楚这是否是扩展问题的解决方案。
随机算法扩展性更好
事实上,在机器学习的背景中,优化成本函数所需的迭代次数不是主要问题:把模型优化至完美是没有意义的,因为基本上都会“过拟合”训练数据。那么,为什么不减少优化模型所需的计算量,而把精力投入到处理更多的数据呢?
Léon 和 Olivier 的工作是对该现象的正式研究:他们考虑访问大量的数据,并假设限制因素是计算,研究结果表明,最好对每个独立训练样本进行最少量的计算(因而可以处理更多样本),而不是对较少量的数据进行大量的计算。
在这个过程中,他们还证明,在各种可能的优化算法中,随机梯度下降法是最佳算法。这已被很多实验所证实,并引起了人们对在线优化算法的兴趣。如今,在线优化算法已广泛应用在机器学习中。
未解之谜
在随后的几年中,随机梯度下降法在凸优化和非凸优化(特别适合于深度学习)场景中发展出了许多变体。现在最常见的变体是所谓的“小批量(mini-batch)”随机梯度下降法,每次迭代只考虑少量的训练样本(大概是 10 到 100 个之间),在训练集上执行多遍,并利用一些聪明的技巧来适当地扩展梯度。大多数机器学习库提供这类算法的默认实现,它被认为是深度学习的支柱之一。
尽管该分析为理解这个算法的特性提供了坚实的基础,但是,深度学习令人难忘甚至有时令人惊讶的成功不断地向科学界提出更多的问题。具体来说,尽管该算法在泛化深度网络特性中的作用已经被反复证明,但我们仍然未能充分理解。这意味着,还有很多有趣的问题等待我们探索,这些问题有助于我们更好地理解目前在使用的算法,并在未来开发出更高效的算法。
10 年前,Léon 和 Olivier 在合作中提出的观点显著推动了现如今已成为机器学习系统主力、造福我们日常生活的算法的发展。我们衷心祝贺两位作者获得这一当之无愧的奖项。
原文链接:
https://ai.googleblog.com/2018/12/the-neurips-2018-test-of-time-award.html