上一篇讲了path的基本用法,这篇我们要去实现水波纹以及粘性小球
这里就不得不提到贝塞尔曲线
一阶贝塞尔曲线:
Android 提供方法:lineTo()
二阶贝塞尔曲线
二阶贝塞尔曲线有一个控制点 P1 和两个数据点 P0,P2。如下图:
二阶贝塞尔曲线
Android 提供方法:quadTo()
三阶贝塞尔曲线:
三阶贝塞尔曲线有两个控制点 P1,P2 和两个数据点 P0,P3。如下图:
三阶贝塞尔曲线
Android 提供方法:cubicTo()
二阶贝塞尔曲线实现如图效果
实现思路:
- 画出至少两段的波纹
- 使用 ValueAnimator 不断获取平移的值 offset
- 利用 offset 不断的改变波纹的位置
- 画一个圆,取与波纹相交的部分
现在分步骤来说明:
1. 画出至少两段波纹我们首先要画出两段波纹。一段波纹就包含两条曲线。每条曲线我们可以使用 quadTo() 方法来画。
为了更容易理解,请看下图:
水波纹坐标图
mWL 是一段波纹的长度,mCenterY 是屏幕高度的一半。
画第一段波纹的第一条曲线:
mPath.moveTo(-mWL, mCenterY); //将path操作的起点移动到(-mWL,mCenterY)mPath.quadTo((-mWL * 3 / 4) , mCenterY + 60, (-mWL / 2), mCenterY); //画出第一段波纹的第一条曲线
画出第一段波纹的第二条曲线
mPath.quadTo((-mWL / 4) , mCenterY - 60, 0, mCenterY); //画出第一段波纹的第二条曲线
画出第二段波纹的第一条曲线:
mPath.quadTo((mWL /4) , mCenterY + 60, (mWL / 2), mCenterY); //画出第二段波纹的第一条曲线
画出第二段波纹的第二条曲线:
mPath.quadTo((mWL * 3/ 4) , mCenterY - 60, mWL, mCenterY); //画出第二段波纹的第二条曲线
- 使用 ValueAnimator 不断获取平移的值 offset
那么现在来想一下应该怎么让这几段波纹动起来呢?我们需要一个 offset 的平移值。这个值应该加在每个点的x坐标上,并且 offset 是不断变化的,这样才会形成一个向右平移的效果。那怎么才能获取到这个变化的offset的值呢?答案就是要使用 ValueAnimator 。用法如下:
private void initAnimator() {
ValueAnimator animator = ValueAnimator.ofInt(0, mWL);
animator.setRepeatCount(ValueAnimator.INFINITE);
animator.setDuration(2000);
animator.setInterpolator(new LinearInterpolator());
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
offset = (int) animation.getAnimatedValue();
postInvalidate();
}
});
animator.start();
}
这样只要动画开始,offset 就会不断从 0~mWL 变化。
- 利用offset不断的改变波纹的位置
现在为曲线的所有 X 坐标都加上 offset 值。这样就会产生平移的效果,为了简化代码,这里使用的 for 循环来画曲线。
mPath.reset();
mPath.moveTo(-mWL + offset, mCenterY);
for (int i = 0; i < mWaveCount; i++) {
mPath.quadTo((-mWL * 3 / 4) + (i * mWL) + offset, mCenterY + 60, (-mWL / 2) + (i * mWL) + offset, mCenterY);
mPath.quadTo((-mWL / 4) + (i * mWL) + offset, mCenterY - 60, i * mWL + offset, mCenterY);
}
mPath.lineTo(mScreenWidth, mScreenHeight);
mPath.lineTo(0, mScreenHeight);
mPath.close();
canvas.setDrawFilter(pfd);
canvas.drawPath(mPath, mPaint);
现在,我们已经得到了波浪
这里我们可以用
mPath.op(mPath2, Path.Op.INTERSECT);
但是这样就最低版本只能支持api19,兼容性不好,所以我们要换个思维,使用
canvas.clipPath(mPath, Region.Op.INTERSECT);
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//画圆
canvas.drawCircle(mScreenWidth / 2, mCenterY, 300, mPaint2);
mPath.reset();
mPath.moveTo(-mWL + offset, mCenterY);
for (int i = 0; i < mWaveCount; i++) {
mPath.quadTo((-mWL * 3 / 4) + (i * mWL) + offset, mCenterY + 60, (-mWL / 2) + (i * mWL) + offset, mCenterY);
mPath.quadTo((-mWL / 4) + (i * mWL) + offset, mCenterY - 60, i * mWL + offset, mCenterY);
}
mPath.lineTo(mScreenWidth, mScreenHeight);
mPath.lineTo(0, mScreenHeight);
mPath.close();
mPath2.addCircle(mScreenWidth / 2, mCenterY, 300, Path.Direction.CCW);
//api19以上才能用
// mPath.op(mPath2, Path.Op.INTERSECT);
//改用canvas.clipPath
canvas.clipPath(mPath, Region.Op.INTERSECT);
canvas.setDrawFilter(pfd);
canvas.drawPath(mPath2, mPaint);
}
成功画出
三阶贝塞尔曲线的应用:
贝塞尔曲线知识讲解
将这个圆的动画效果拆解开看的画,其实会分为5个状态。
pic1.png-2kB
状态1
pic2.png-2.4kB
状态2
pic3.png-2.6kB
状态3
pic4.png-2.4kB
状态4
pic1.png-2kB
状态5注:我这里的状态4和状态5其实与原设计图是有出入的,我这里的5个状态其实是对称关系的,但是原设计图并非是对称关系,然后因为我偷懒,就做成了对称设计,这个以后再优化吧~
也就是说,这个动画效果的实现就是不同状态之间的转化加上水平位移的实现,现在已经将动画肢解完了,那么接下来就讲解下如何实现圆的形变吧。
开始讲解具体内容之前我们需要先了解一下如何用贝塞尔曲线画一个圆,因为我的做法是通过贝塞尔曲线来实现的。
stackoverflow
上图是stackoverflow上的一个答案,这个答案可能说的不是很清楚,这里还有一篇文章,这两个的结果都是差不多,就是所需要的数值c约等于0.551915024494f,具体的论证过程可以看这两篇文章,那么这个c的值有什么用么,我用最简单的方法来说明,就是把图中的1理解为圆的半径,那么对应的另外个值就应该是半径乘以0.551915024494f。可能有朋友还是看不懂这个c到底干啥用呢,我下面画一个图来描述下,大概是怎么个意思。
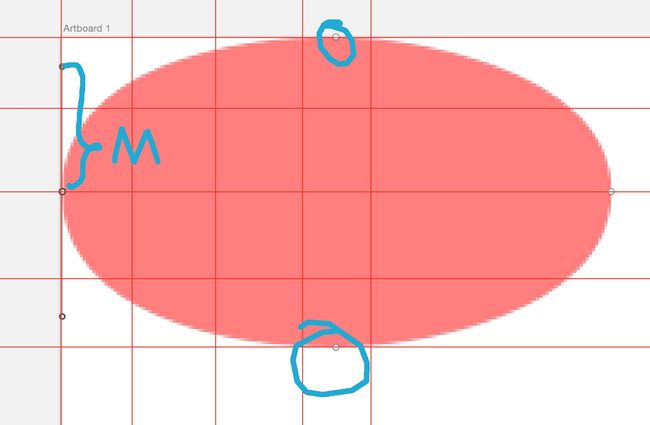
这里的坐标轴也就是Android中的坐标轴了,如果我们打算用贝塞尔曲线来画这么一个圆的话,我们需要知道这个圆的半径,以及图中的M的值,知道这两个值的话就能够知道图中12个点的坐标,知道坐标就能够用Path的cubicTo方法来使用贝塞尔曲线画出圆了。这里稍微展示点代码来说明如何绘制P0至P3这段圆弧。
mPath.moveTo(p0.x,p0.y);mPath.cubicTo(p1.x, p1.y, p2.x, p2.y, p3.x,p3.y);
这样我们就知道如何使用贝塞尔曲线来绘制一个圆了。也就是状态1和状态5我们都会绘制了,接下来看看状态2如何绘制。
jiangjietu2.png-108.1kB
通过上图大家就能很快的明白状态2应该如何绘制,其实就是把右边的点向右移动点距离就行了。其实photoshop(sketch)这些绘图软件中的钢笔工具(Vector)就是用的贝塞尔曲线,然后这里推荐个网址给大家,轻松上手钢笔工具的使用哦,强烈推荐!!!
看完上面的讲解,那么状态3也就一点都不难了。
看到上图就明白状态3的实现就是在状态2的基础上修改了个值,一个是M的值加大,让圆看起来跟肥一点,还有就是圈住的那些点向右移动,做到居中。
github代码下载
也欢迎关注我的CSDN和github主页