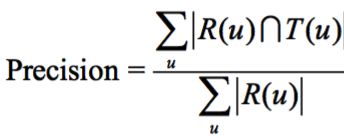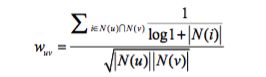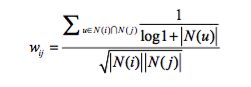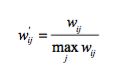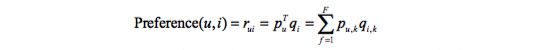利用用户行为数据分析的算法也称为协同过滤算法
用户行为日志通常存储在分布式数据仓库中,如支持离线分析的Hadoop Hive和支持在线分析的Google Dremel。
用户行为分为显性反馈行为(explicit feedback)和隐性反馈行为(implicit feedback),举几个例子来解释下这两个名词:
用户行为的一般规律
很多网站的普遍规律表明,用户行为大都遵循长尾分布
学术界对协同过滤算法进行了深入研究,提出了很多方法,比如基于邻域的方法(neighborhood-based)、隐语义模型 (latent factor model)、基于图的随机游走算法(random walk on graph)等。在这些方法中, 最著名的、在业界得到最广泛应用的算法是基于邻域的方法,而基于邻域的方法主要包含下面两种算法:
- 基于用户的协同过滤算法 : 这种算法给用户推荐和他兴趣相似的其他用户喜欢的物品。
- 基于物品的协同过滤算法 : 这种算法给用户推荐和他之前喜欢的物品相似的物品。
实验设计和算法评测
数据集
这里离线实验的数据集采用GroupLens提供的MovieLens数据集。实验设计
首先,将用户行为数据集按照均匀分布随机分成M 份(例如取M=8),挑选一份作为测试集,将剩下的M-1份作为训练集。
然后在训练集上建立用户兴趣模型,并在测试集上对用户行为进行预测,统计出相应的评测指标。
为了保证评测指标并不是过拟合的结果,需要进行M次实验,并且每次都使用不同的测试集。然后将M次实验测出的评测指标的平均值作为最终的评测指标。
def SplitData(data, M, k, seed):
test = []
train = []
random.seed(seed)
for user, item in data:
if random.randint(0,M) == k:
test.append([user,item])
else:
train.append([user,item])
return train, test
这里,每次实验选取不同的k(0≤k≤M1)和相同的随机数种子seed,进行M次实验就可以得到M个不同的训练集和测试集,然后分别进行实验,用M次实验的平均值作为最后的评测指标。
- 评测指标
可通过准确率和召回率评测推荐算法的精度(基础概念学习):
准确率
def Precision(train, test, N):
hit = 0
all = 0
for user in train.keys():
tu = test[user]
rank = GetRecommendation(user, N)
for item, pui in rank: 4
if item in tu:
hit += 1
all += N
return hit / (all * 1.0)
召回率
def Recall(train, test, N):
hit = 0
all = 0
for user in train.keys():
tu = test[user]
rank = GetRecommendation(user, N)
for item, pui in rank:
if item in tu:
hit += 1
all += len(tu)
return hit / (all * 1.0)
覆盖率反映了推荐算法发掘长尾的 能力,覆盖率越高,说明推荐算法越能够将长尾中的物品推荐给用户。
def Coverage(train, test, N):
recommend_items = set()
all_items = set()
for user in train.keys():
for item in train[user].keys():
all_items.add(item)
rank = GetRecommendation(user, N)
for item, pui in rank:
recommend_items.add(item)
return len(recommend_items) / (len(all_items) * 1.0)
新颖度这里用推荐列表中物品的平均流行度度量推荐结果的新颖度。如果推荐出的物品都很热门,说明推荐的新颖度较低,否则说明推荐结果比较新颖。
def Popularity(train, test, N):
item_popularity = dict()
for user, items in train.items():
for item in items.keys()
if item not in item_popularity:
item_popularity[item] = 0
item_popularity[item] += 1
ret = 0
n=0
for user in train.keys():
rank = GetRecommendation(user, N)
for item, pui in rank:
ret += math.log(1 + item_popularity[item])
n += 1
ret /= n * 1.0
return ret
重点:
基于邻域的算法
- 基于用户的协同过滤算法
(1) 找到和目标用户兴趣相似的用户集合。
(2) 找到这个集合中的用户喜欢的,且目标用户没有听说过的物品推荐给目标用户。
用户相似度简单计算:
协同过滤算法主要利用行为的相似度计算兴趣的相似度。给定用户u和用户v,令N(u)表示用户u曾经有过正反馈的物品集合,令N(v)为用户v曾经有过正反馈的物品集合。
或者通过余弦相似度计算:
举个例子解释一下:UserCF计算用户兴趣相似度的例子。在该 例中,用户A对物品{a, b, d}有过行为,用户B对物品{a, c}有过行为,利用余弦相似度公式计算用 户A和用户B的兴趣相似度为:
对两两用户都利用余弦相似度计算相似度。这种方法的时间复杂度是O(|U|*|U|),这在 用户数很大时非常耗时。事实上,很多用户相互之间并没有对同样的物品产生过行为,即很多时 候 N (u) 相交 N (v)等于 0 。
可以首先建立物品到用户的倒排表,对于每个物品都保存对该物品产生过行为的用户列表。令稀疏矩阵C[u][v]= N (u) 交 N (v) 。那么,假设用户u和用户v同时属于倒排表中K个物品对 应的用户列表,就有C[u][v]=K。从而,可以扫描倒排表中每个物品对应的用户列表,将用户列 表中的两两用户对应的C[u][v]加1,最终就可以得到所有用户之间不为0的C[u][v]。
def UserSimilarity(train):
# build inverse table for item_users
item_users = dict()
for u, items in train.items():
for i in items.keys():
if i not in item_users:
item_users[i] = set()
item_users[i].add(u)
#calculate co-rated items between users
C = dict()
N = dict()
for i, users in item_users.items():
for u in users:
N[u] += 1
for v in users:
if u == v:
continue
C[u][v] += 1
#calculate finial similarity matrix W
W = dict()
for u, related_users in C.items():
for v, cuv in related_users.items():
W[u][v] = cuv / math.sqrt(N[u] * N[v])
return W
得到用户之间的兴趣相似度后,UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的 物品。如下的公式度量了UserCF算法中用户u对物品i的感兴趣程度:
S(u, K)包含和用户u兴趣最接近的K个用户,N(i)是对物品i有过行为的用户集合,wuv 是用户u和用户v的兴趣相似度,rvi代表用户v对物品i的兴趣,因为使用的是单一行为的隐反馈数 据,所以所有的rvi=1。
选取K=3,用户A对物品c、e没有过行为, 因此可以把这两个物品推荐给用户A。根据UserCF算法,用户A对物品c、e的兴趣是:
p(A,c) = wAB+ wAD = 0.7416
p(A,e) = wAC + wAD = 0.7416
用户相似度计算改进:
以图书为例,如果两个用户都曾经买过《新华字典》,这丝毫不能说明他们兴趣相似, 因为绝大多数中国人小时候都买过《新华字典》。但如果两个用户都买过《数据挖掘导论》,那可 以认为他们的兴趣比较相似,因为只有研究数据挖掘的人才会买这本书。换句话说,两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度。
该算法减小了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。
比较上面的算法,只是在计算C[u][v]加1时做了改变:
//简单版
C[u][v] += 1
//优化版
C[u][v] += 1 / math.log(1 + len(users))
- 基于物品的协同过滤算法
基础算法
ItemCF算法并不利用物品的内容属性计算物品之间的相似度,它主要通过分析用户的行为记录计算物品之间的相似度。该算法认为,物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。
1、基于物品的协同过滤算法主要分为两步。
(1) 计算物品之间的相似度。
(2) 根据物品的相似度和用户的历史行为给用户生成推荐列表。
分母|N(i)|是喜欢物品i的用户数,而分子 N(i)N(j) 是同时喜欢物品i和物品j的用户 数。因此,上述公式可以理解为喜欢物品i的用户中有多少比例的用户也喜欢物品j。虽然看起来很有道理,但是却存在一个问题。如果物品j很热门,很多人都喜欢,那么Wij就会很大,接近1。
这个公式惩罚了物品j的权重,因此减轻了热门物品会和很多物品相似的可能性。
和UserCF算法类似,用ItemCF算法计算物品相似度时也可以首先建立用户—物品倒排表(即 对每个用户建立一个包含他喜欢的物品的列表),然后对于每个用户,将他物品列表中的物品两 两在共现矩阵C中加1。
在得到物品之间的相似度后,ItemCF通过如下公式计算用户u对一个物品j的兴趣:
这里N(u)是用户喜欢的物品的集合,S(j,K)是和物品j最相似的K个物品的集合,wji是物品j和i 的相似度,rui是用户u对物品i的兴趣。(对于隐反馈数据集,如果用户u对物品i有过行为,即可令 5 rui=1。)
2、用户活跃度对物品相似度的影响:
活跃用户对物品相似度的贡献应该小于不活跃的用户\
上面的公式只是对活跃用户做了一种软性的惩罚 。
3、物品相似度的归一化
如果已经得到了物品相似度矩阵w,那么可以用如下公式得到归一化之后的相似度 矩阵w':
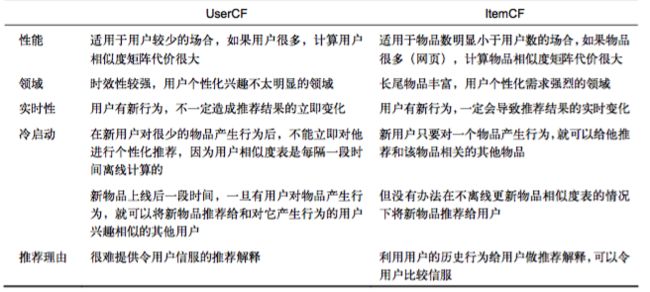
UserCF和ItemCF的综合比较
UserCF的推荐结果着重于反映和用户兴趣相似的小群体的热点,而ItemCF 的推荐结果着重于维系用户的历史兴趣。换句话说,UserCF的推荐更社会化,反映了用户所在的小型兴趣群体中物品的热门程度,而ItemCF的推荐更加个性化,反映了用户自己的兴趣传承。
隐语义模型
LFM(latent factor model)隐语义模型通过如下公式计算用户u对物品i的兴趣:
这个公式中 Pu,k 和 qi,k 是模型的参数,其中 Pu,k 度量了用户u的兴趣和第k个隐类的关系,而 qi,k 度量了第k个隐类和物品i之间的关系。这两 个参数是从数据集中计算出来的。
对负样本采样时应该 遵循以下原则:
- 对每个用户,要保证正负样本的平衡(数目相似)。
- 对每个用户采样负样本时,要选取那些很热门,而用户却没有行为的物品。
def RandomSelectNegativeSample(self, items):
ret = dict()
for i in items.keys():
ret[i] = 1
n=0
for i in range(0, len(items) * 3):
item = items_pool[random.randint(0, len(items_pool) - 1)]
if item in ret:
continue
ret[item] = 0
n+=1
if n > len(items):
break
return ret
LFM和基于邻域的方法的比较
LFM是一种基于机器学习的方法,具有比较好的理论基础。这个方法和基于邻域的方法(比 如UserCF、ItemCF)相比,各有优缺点。
理论基础LFM具有比较好的理论基础,它是一种学习方法,通过优化一个设定的指标 建立最优的模型。基于邻域的方法更多的是一种基于统计的方法,并没有学习过程。离线计算的空间复杂度基于邻域的方法需要维护一张离线的相关表。在离线计算相关表的过程中,如果用户/物品数很多,将会占据很大的内存。假设有M个用户和N个物品, 在计算相关表的过程中,我们可能会获得一张比较稠密的临时相关表(尽管最终我们对 每个物品只保留K个最相关的物品,但在中间计算过程中稠密的相关表是不可避免的), 那么假设是用户相关表,则需要O(MM)的空间,而对于物品相关表,则需要O(NN)的空 间。而LFM在建模过程中,如果是F个隐类,那么它需要的存储空间是O(F*(M+N)),这在 M和N很大时可以很好地节省离线计算的内存。在Netflix Prize中,因为用户数很庞大
(40多万),很少有人使用UserCF算法(据说需要30 GB左右的内存),而LFM由于大量节 省了训练过程中的内存(只需要4 GB),从而成为Netflix Prize中最流行的算法。离线计算的时间复杂度假设有M个用户、N个物品、K条用户对物品的行为记录。那么, UserCF计算用户相关表的时间复杂度是O(N * (K/N)^2),而ItemCF计算物品相关表的时间 复杂度是O(M(K/M)^2)。而对于LFM,如果用F个隐类,迭代S次,那么它的计算复杂度 是O(K * F * S)。那么,如果K/N > FS,则代表UserCF的时间复杂度低于LFM,如果 K/M>F*S,则说明ItemCF的时间复杂度低于LFM。在一般情况下,LFM的时间复杂度要 稍微高于UserCF和ItemCF,这主要是因为该算法需要多次迭代。但总体上,这两种算法 在时间复杂度上没有质的差别。在线实时推荐UserCF和ItemCF在线服务算法需要将相关表缓存在内存中,然后可以在 线进行实时的预测。以ItemCF算法为例,一旦用户喜欢了新的物品,就可以通过查询内 存中的相关表将和该物品相似的其他物品推荐给用户。因此,一旦用户有了新的行为, 而且该行为被实时地记录到后台的数据库系统中,他的推荐列表就会发生变化。而从LFM 的预测公式可以看到,LFM在给用户生成推荐列表时,需要计算用户对所有物品的兴趣 权重,然后排名,返回权重最大的N个物品。那么,在物品数很多时,这一过程的时间 复杂度非常高,可达O(MNF)。因此,LFM不太适合用于物品数非常庞大的系统,如 果要用,我们也需要一个比较快的算法给用户先计算一个比较小的候选列表,然后再用 LFM重新排名。另一方面,LFM在生成一个用户推荐列表时速度太慢,因此不能在线实 时计算,而需要离线将所有用户的推荐结果事先计算好存储在数据库中。因此,LFM不 能进行在线实时推荐,也就是说,当用户有了新的行为后,他的推荐列表不会发生变化。推荐解释ItemCF算法支持很好的推荐解释,它可以利用用户的历史行为解释推荐结果。 但LFM无法提供这样的解释,它计算出的隐类虽然在语义上确实代表了一类兴趣和物品, 却很难用自然语言描述并生成解释展现给用户。
基于图的模型
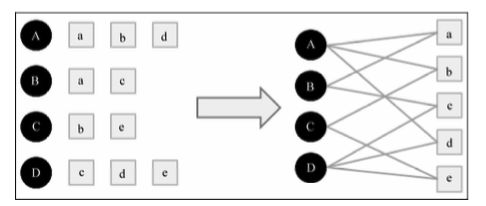
下图是一个简单的用户物品二分图模型,其中圆形节点代表用户,方形节点代表物品,圆形节点和方形节点之间的边代表用户对物品的行为。比如图中用户节点A和物品节点a、b、d相连,说明用户A对物品a、b、d产生过行为。
基于图的推荐算法:
- 两个顶点之间有很多路径相连;
- 连接两个顶点之间的路径长度都比较短;
- 连接两个顶点之间的路径不会经过出度比较大的顶点。