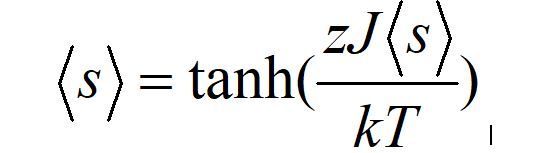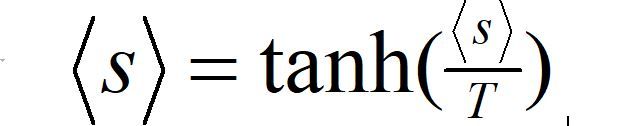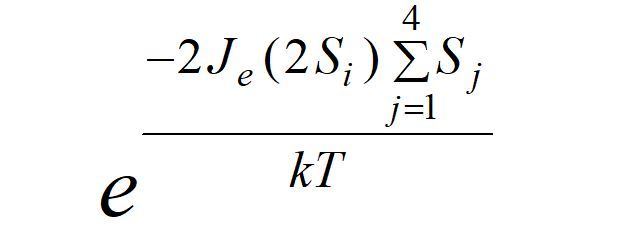期末作业,选择了热力学与统计物理学中的内容,一方面完成了课程考核,另一方面捎带复习热统。主要是和教材中伊辛模型 相关的热力学与统计物理学中的内容,编程画图分析得结论。
一,摘要
相变和临界现象是一个跨学科领域,在连续相变的临界点,热力学函数和关联函数呈现奇异性,他们来源于粒子间的相互作用。在热统中,处理系统性问题时往往将微观粒子之间的相互作用作为小项而忽略掉,且称这种粒子系统为近独立子系,但在某些情况下,系统的粒子之间的相互作用不可忽略,甚至在系统中起着重要作用,此时就再也不能将其忽略掉了。例如物质的铁磁性就是粒子间较强相互作用引起的,处理此类系统问题时便不能再忽略掉粒子间相互作用,而伊辛模型就是一种描写磁系统相变的模型,本文通过数值方法来研究伊辛模型。
二,分析与编程
对于自旋系统,应用最近邻近似法,再以一个与复杂自旋耦合效果等价的平均力场来代替耦合,对于粒子 i,计及其周围共 Z 个粒子的影响,以场 B_e来代替这 Z 个粒子对粒子 i 的共同耦合效果。下面公式,左边为最近邻自旋下对粒子 i 的能量 E,右边为以平均力场 B_e 作用于粒子 i 后附加的能量 E
以上引用热统中的内容来引入概念和方法,下面开始问题的正式解决。
对于由自旋为 1 的粒子,对于一个特定的空间取向,其自旋呈现只有 +1 和 -1 的变化
本课程教材中通过分析和简化,同时应用分子场近似(平均力场)得出结论公式
为参量取某指定值时的平均自旋,J 为交换系数,k 为玻尔兹曼常数,T 为对应温度,z 为最近邻粒子数目。
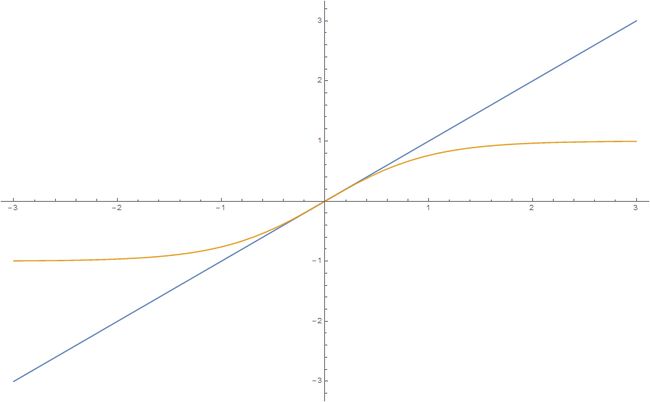
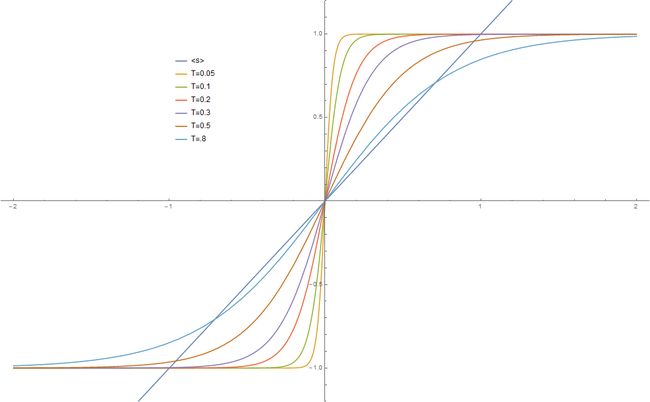
简单分析以上公式外加联系以上函数的曲线特征可知,在 z , T , J 都为稳定值时,等式两边的函数图像一般存在三个交点,如下图:
但是当 tanh 函数在原点的斜率与直线斜率 y = 相等时,便只存在一个交点,即等式只存在一个解 =0 ,由平均场 H' 的定义式
则 =0 该情况则对应着 H' =0 ,即磁场为 0,没有自发磁化现象发生。由一个简单的推导可知,此时对应的温度 T = z*J/k 。
下面根据公式画出不同温度下曲线的交点情况,假设 a = zJ/k ,取 a为 1(因为我们的图像模拟只需要的是一种变化的趋势,故常数项 a的具体值无关紧要,取为正数即可,若要具体真实的情况,则将z,J,k代入得到a即可)
公式改造为:
当 T大于临界值时,以此绘图有:
当 T取为小于临界 T值时,有关系图:
由以上绘图可知,当温度 T 大于临界值时,直线与曲线是没有非零交点的,亦即此时物质无自发磁化现象发生。而当温度小于临界温度时,在一定范围内温度越低,交点越接近 1 和 -1,即越来越接近完全的自发磁化(因为 s 最大值就是 1 ),=1 即对应着磁化方向与取定方向同向,=-1 意味着与取定方向完全反向。由图可发现当温度低到一定程度时,在此温度以下的温度时,都是发生完全磁化
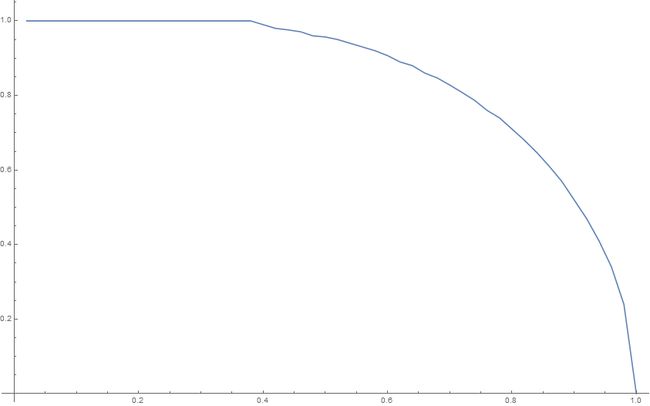
由于原方程解析解不能求出,故用数值方法对不同温度下的方程求解得 值
用Mathematica寻根命令:
Table[FindRoot[x == Tanh[x/a], {x, 1}], {a, 0.02, 1, 0.02}]
得方程的几个温度下的解:
{x -> 1.}, {x -> 1.}, {x -> 1.}, {x -> 1.}, {x -> 1.}, {x -> 1.}, {x -> 0.999999}, {x -> 0.999993}, {x -> 0.99997}, {x -> 0.999909}, {x -> 0.999774}, {x -> 0.999517}, {x -> 0.999081}, {x -> 0.998402}, {x -> 0.997414}, {x -> 0.99605}, {x -> 0.994248}, {x -> 0.991947}, {x -> 0.98909}, {x -> 0.985624}, {x -> 0.981499}, {x -> 0.976669}, {x -> 0.971089}, {x -> 0.964715}, {x -> 0.957504}, {x -> 0.949413}, {x -> 0.940398}, {x -> 0.930412}, {x -> 0.919408}, {x -> 0.907332}, {x -> 0.894128}, {x -> 0.879732}, {x -> 0.864073}, {x -> 0.847072}, {x -> 0.828635}, {x -> 0.808656}, {x -> 0.78701}, {x -> 0.763548}, {x -> 0.738089}, {x -> 0.710412}, {x -> 0.680241}, {x -> 0.64722}, {x -> 0.610884}, {x -> 0.570591}, {x -> 0.52543}, {x -> 0.474002}, {x -> 0.413976}, {x -> 0.340829}, {x -> 0.242983}, {x -> 2.25808*10^-8}
画图有:
由上图可见,在一定范围温度内, 保持完全磁化状态,当温度超过某值后开始下降,且下降趋势越来越快,当达到临界温度(对应横坐标为 1.0 )后自发磁化现象消失。
用蒙特卡洛方法对磁系统的研究
本部分由教材内容直接应用,简略描述为:自旋 s_i 受其周围诸最近邻自旋 s_j 的影响,会发生取向反转,对于二维方格子情形,因为自旋在只在给定方向上取值 ±1 ,所以之前的能量公式由矢量式退化为标量式:
选取一包含方阵结构一定数量自旋粒子的方格子,粒子 i 受周围最近邻作用:
应用蒙特卡洛方法的原理 是,先给定一个格子内部各自旋的初始分布,以粒子 i 为例,当其自旋反转时,则显然能量 E 的值会变化,自旋反转前后能量的变化值:
对上式的解释:E' 即反转后能量,E_0 则为原能量。将 ΔE 代入到玻尔兹曼因子 e^(-ΔE/kT)中。改写为
由随机数发生器产生 [0,1] 之间的随机数。ΔE > 0 时,当随机数小于上式值时 S_ i 反转,当随机数大于上式值时 S_ i 不反转;而当 ΔE ≤ 0 时,S_ i反转,边界处应用周期性边界条件,以此规则编程即可。编程时以 t = 2J/kT 为自变量。
t = 5; l = Length[s]; list = {};
Do[s = Table[{1, -1, 1, 1, -1, 1, -1, -1, 1, -1, 1, -1, 1, -1, -1, 1,1, -1, 1, -1, 1, -1, 1, -1, 1, -1, 1, 1, -1, 1}, 30];
sum = Total[Flatten[s]] - 100;
While[Abs[Total[Flatten[s]] - sum] >= 1, sum = Total[Flatten[s]];
For[i = 1, i <= 30, i++,
For[j = 1, j <= 30, j++,
If[i == 1 && j >= 2 && j <= l - 1,
dE = 2 s[[i,j]]*(s[[l, j]] + s[[i + 1, j]] + s[[i, j - 1]] + s[[i, j + 1]]), Null];
If[i == l && j >= 2 && j <= l - 1, dE = 2 s[[i, j]]*(s[[i - 1, j]] + s[[1, j]] + s[[i, j - 1]] +s[[i, j + 1]]), Null];
If[j == 1 && i >= 2 && i <= l - 1,dE = 2 s[[i, j]]*(s[[i - 1, j]] + s[[i + 1, j]] + s[[i, l]] + s[[i, j + 1]]), Null];
If[j == l && i >= 2 && i <= l - 1,dE = 2 s[[i, j]]*(s[[i - 1, j]] + s[[i + 1, j]] + s[[i, j - 1]] +s[[i, 1]]), Null];
If[i == 1 && j == 1,dE = 2 s[[i, j]]*(s[[l, j]] + s[[i + 1, j]] + s[[i, l]] + s[[i, j + 1]]), Null];
If[i == 1 && j == l,dE = 2 s[[i, j]]*(s[[l, j]] + s[[i + 1, j]] + s[[i, j - 1]] + s[[i, 1]]),Null];
If[i == l && j == l, dE = 2 s[[i, j]]*(s[[i - 1, j]] + s[[1, j]] + s[[i, j - 1]] + s[[i, 1]]), Null];
If[i == l && j == 1, dE = 2 s[[i, j]]*(s[[i - 1, j]] + s[[1, j]] + s[[i, l]] + s[[i, j + 1]]), Null];
If[i > 1 && j > 1 && i < l && j < l, dE = 2 s[[i, j]]*(s[[i - 1, j]] + s[[i + 1, j]] + s[[i, j - 1]] +
s[[i, j + 1]]), Null];
If[dE <= 0 || E^(-t*dE) >= RandomReal[], s[[i, j]] = -s[[i, j]], Null]
]]]; AppendTo[list, sum/l^2], 100];
ListPlot[list]
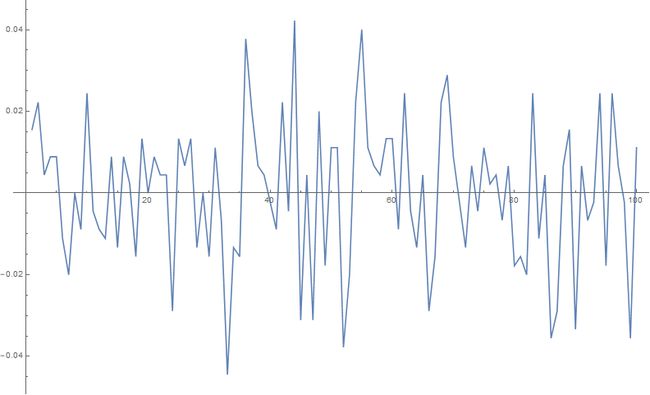
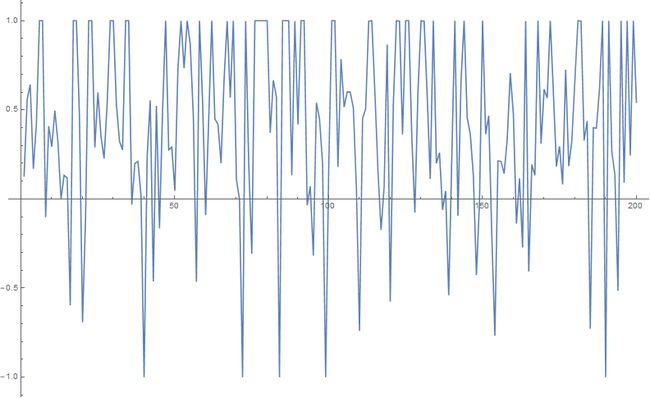
以上编程中取了一个30*30的自旋方格子,运行结果:
t=0.1
t=0.5
t=1
t=2
可以看到随着t的增大(因为 t 与温度 T 是反比关系,所以随着 t 的增大亦即随着温度 T 的减小),自发磁化现象越来越明显。在温度T较高时震荡较大,且是围绕着无自发磁化震荡,而随着温度T的减小,自发磁化开始出现,且较明显。由上图即可直观地发现温度与自发磁化(方格子自选统计量)的关系。以上即运用了蒙特卡洛方法研究伊辛模型的模拟结果。
三,总结
本作业主要做了两件事,一个是应用一般数值方法 研究磁系统的自发磁化强度随温度的变化,二是应用所谓的蒙特卡洛方法 研究自旋方格子内的磁化强度随温度的变化
通过模拟得到了一些结论,因为伊辛模型的精确解难以求解,而计算机的告诉数值运算能力便应用解决了这一瓶颈。从以上模拟中,能看出自旋间相互作用随外界温度的变化情况,符合理论上的定性描述,而一些关键相变电也被数值方法描述了出来,总而言之,此次数值模拟是验证了理论的正确性,也能看出,数值模拟能弥补解析方法的不足,带来一些直观的图像。
四,说明
参考文献有:
本课程教材
武汉大学出版社 胡承正《热力学与统计物理学》
二维Ising模型临界相变的Monte-Carlo数值模拟(《安徽大学学报:自然科学版》2008年 第3期 | 李晓寒 王宗笠 宁旭 )
作业最后一次更新于2017/12/28,并于该日将pdf文件邮件发至老师邮箱[email protected]