翻译:非常详细易懂的法线贴图(Normal Mapping)
- 本文翻译自: Shaders » Lesson 6: Normal Mapping
- 作者: Matt DesLauriers
- 译者: FreeBlues
这一系列依赖于最小规模的用于着色器和渲染工具的lwjgl-basics API.
代码已经被移植到 LibGDX. 这些概念是足够通用的, 它们能被应用于Love2D, GLSL Sandbox, iOS, 或者其他支持 GLSL 的平台.
概述
本文聚焦于 3D 光照和法线贴图技术, 以及我们如何把它们应用到 2D 游戏中, 示范下图所示, 左边是纹理贴图, 右边实时应用了光照:
一旦你理解了光照的概念, 把它应用于任何设置都是非常直截了当的. 这里是一个 Java4K 示例中的法线贴图的例子, 例如, 通过软件渲染:
效果跟这个 YouTube流行视频 和这个 Love2D示例 中展示的一样, 你还可以在 [GLSL] Using Normal Maps to Illuminate a 2D Texture (LibGDX) 看到效果, 其中包括一个可执行的示例.
介绍向量和法线
正如我们在之前的教程中讨论过的, 一个 GLSL 向量是一个浮点数的容器, 通常保存诸如位置(x,y,z)之类的值. 在数学中,向量意味着相当多的内容,以及用于表示长度(即大小)和方向. 如果你对向量很陌生并且想要学习关于它们更多一些的知识, 查看下面这些链接:
- Basic 3D Math
- Vector Math for Graphics
- Mathematics of Vectors Applied to Graphics
为了计算光照, 我们需要使用网格的"法线". 一个表面法线是一个垂直于切线平面的向量. 简单来说, 它是一个向量, 垂直于给定顶点处的网格. 下面我们会看到一个网格, 每个顶点都有一条法线.
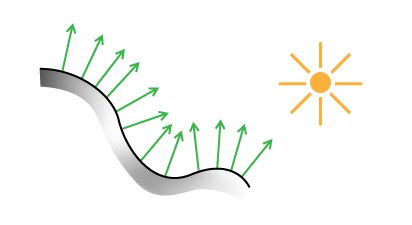
每个向量都指向外面, 遵循着网格的弯曲形状. 下面是另一个例子, 这次是一个简单的 2D 边沿视图:
法线贴图(Normal Mapping)是一个游戏编程技巧, 它允许我们渲染相同数目的多边形(例如低解析度的网格模型), 但是在计算光照时使用高解析度网格模型的法线. 这为我们带来更好的感受, 关于深度, 真实性和光滑度.
(图像来自于这个出色的博客文章Making Worlds 3 - That's no Moon...)
高面数网格模型或者说精雕模型的法线被编码到一个纹理贴图(即法线图)中, 当我们渲染低面数网格模型时会从片段着色器中对它进行取样. 结果如下:
译者注: 左侧是4百万个三角形的高模, 中间是500个三角形的低模, 右侧是在500个三角形的低模上使用法线贴图后的效果
对法线编码和解码
我们的表面法线是单位向量, 通常位于范围 -1.0 到 1.0 之间. 我们可以通过把法线范围转换为 0.0 到 1.0之间来把法线向量(x, y, z)存储到一个 RGB 纹理贴图中. 下面是伪码:
Color.rgb = Normal.xyz / 2.0 + 0.5;例如, 一个法线 (-1, 0, 1) 会被作为 RGB 编码为 (0, 0.5, 1). x 轴(左/右)被保存到红色通道, y 轴(上/下)被保存到绿色通道, z 轴(前/后)被保存到蓝色通道. 最终的法线图(normal map)看起来就是下面这个样子:
典型地, 我们使用程序来生成法线图, 而不是手动绘制.
理解法线图, 把每个通道独立出来查看会更清楚:
看着,绿色通道,我们看到更亮的部分(值更接近于 1.0) 定义了法线指向上方的区域,而更暗的区域(值更接近为 0.0) 定义了法线指向下方的区域. 大多数的法线图会是蓝色,因为Z轴(蓝色通道)通常指向我们(即值为 1.0).
在我们游戏的片段着色器中, 我们可以把法线解码, 通过执行跟之前编码时相反的操作, 把颜色值展开为范围 -1.0 到 1.0 之间:
//sample the normal map
NormalMap = texture2D(NormalMapTex, TexCoord);
//convert to range -1.0 to 1.0
Normal.xyz = NormalMap.rgb * 2.0 - 1.0;注意: 要记住不同的引擎和软件会使用不同的坐标系, 绿色通道可能需要翻转.
Lambertian 光照模型
在计算机图形学中, 我们有大量的算法,可以结合起来打造 3D 对象的不同渲染效果. 在这篇文章我们将专注于 Lambert 着色,没有任何反射(诸如"光泽"或"发光"). 其他的技术,像Phong, Cook-Torrance, 和 Oren–Nayar, 可以用来产生不同的视觉效果(粗糙表面、 有光泽的表面等等)。
我们整个光照模型看起来像这样:
N = normalize(Normal.xyz)
L = normalize(LightDir.xyz)
Diffuse = LightColor * max(dot(N, L), 0.0)
Ambient = AmbientColor * AmbientIntensity
Attenuation = 1.0 / (ConstantAtt + (LinearAtt * Distance) + (QuadraticAtt * Distance * Distance))
Intensity = Ambient + Diffuse * Attenuation
FinalColor = DiffuseColor.rgb * Intensity.rgb说实话,你不需要从数学角度理解为什么这个可以起作用,但如果你有兴趣, 可以阅读更多有关"N dot L"的内容, 在这里GLSL Tutorial – Directional Lights per Vertex I和这里Lambertian reflectance.
一些关键的术语:
Normal-法线: 从法线图中解码得到的法线向量 XYZ.LightDir-光线方向: 从物体表面到光源位置的向量, 我们将会简单解释.Diffuse Color-漫射颜色: 纹理贴图的 RGB 颜色, 没有光.Diffuse-漫射: 跟Lambertian反射相乘的光线颜色, 这是我们光照等式的主要部分.Ambient-环境光: 处于阴影中的颜色和强度, 例如, 一个户外场景会有一个更亮的环境光强度, 比起一个暗淡灯光下的户内场景.Attenuation-衰减: 这是光线的随距离而降低, 例如, 当我们远离点光源时强度/亮度的损失. 有多种方法来计算衰减--对于我们的目标而言, 我们将会使用常量-线性-二次方衰减. 这里用3个系数来计算衰减, 我们可以改变它们来影响光线衰减的视觉效果.Intensity-强度: 我们阴影算法的强度--离1.0越近意味着有光, 离0.0越近意味着没有光.
下面的图有助于你对我们的光照模型有个直观的理解:
正如你所见, 感觉它是相当模块化的, 我们可以拿走那些不需要的部分, 就像衰减(attenuation) 或光线颜色(light colors).
现在, 让我们把它们应用到 GLSL 模型上. 注意我们只处理 2D, 在 3D 中还有一些额外的考虑在这篇教程没有覆盖到(译者注:就是空间变换, 在 3D 场景下, 法线图中的法线所在的空间为正切空间, 光线所在的空间为世界空间, 需要统一到同一个空间计算才有意义). 我们将把模型分解为多个单独部分, 每一个都建立在下面的基础上.
Java 例程
你可以在这里看到Java代码示例. 它是相对直截了当的, 并不会介绍过多的在在前面的课程中还没有讨论过的内容. 我们将使用以下两种纹理贴图︰
我们的示例根据鼠标位置(归一化到分辨率)调整 LightPos.xy, 根据鼠标滚轮(点击则重置光线的 Z值)调整 LightPos.z(深度). 在特定的坐标系中, 就像 LibGDX, 你可能需要翻转 Y 值.
注意, 我们的例子使用了如下这些常量, 你可以调整它们来获得不同的视觉效果:
public static final float DEFAULT_LIGHT_Z = 0.075f;
...
//Light RGB and intensity (alpha)
public static final Vector4f LIGHT_COLOR = new Vector4f(1f, 0.8f, 0.6f, 1f);
//Ambient RGB and intensity (alpha)
public static final Vector4f AMBIENT_COLOR = new Vector4f(0.6f, 0.6f, 1f, 0.2f);
//Attenuation coefficients for light falloff
public static final Vector3f FALLOFF = new Vector3f(.4f, 3f, 20f);下面是我们的渲染代码, 就像 教程4 一样, 我们会在渲染时使用多重纹理:
...
//update light position, normalized to screen resolution
float x = Mouse.getX() / (float)Display.getWidth();
float y = Mouse.getY() / (float)Display.getHeight();
LIGHT_POS.x = x;
LIGHT_POS.y = y;
//send a Vector4f to GLSL
shader.setUniformf("LightPos", LIGHT_POS);
//bind normal map to texture unit 1
glActiveTexture(GL_TEXTURE1);
rockNormals.bind();
//bind diffuse color to texture unit 0
glActiveTexture(GL_TEXTURE0);
rock.bind();
//draw the texture unit 0 with our shader effect applied
batch.draw(rock, 50, 50);阴影贴图的结果:
下面对光线使用了更低的 Z 值:
片段着色器
这里是我们完整的片段着色器
//attributes from vertex shader
varying vec4 vColor;
varying vec2 vTexCoord;
//our texture samplers
uniform sampler2D u_texture; //diffuse map
uniform sampler2D u_normals; //normal map
//values used for shading algorithm...
uniform vec2 Resolution; //resolution of screen
uniform vec3 LightPos; //light position, normalized
uniform vec4 LightColor; //light RGBA -- alpha is intensity
uniform vec4 AmbientColor; //ambient RGBA -- alpha is intensity
uniform vec3 Falloff; //attenuation coefficients
void main() {
//RGBA of our diffuse color
vec4 DiffuseColor = texture2D(u_texture, vTexCoord);
//RGB of our normal map
vec3 NormalMap = texture2D(u_normals, vTexCoord).rgb;
//The delta position of light
vec3 LightDir = vec3(LightPos.xy - (gl_FragCoord.xy / Resolution.xy), LightPos.z);
//Correct for aspect ratio
LightDir.x *= Resolution.x / Resolution.y;
//Determine distance (used for attenuation) BEFORE we normalize our LightDir
float D = length(LightDir);
//normalize our vectors
vec3 N = normalize(NormalMap * 2.0 - 1.0);
vec3 L = normalize(LightDir);
//Pre-multiply light color with intensity
//Then perform "N dot L" to determine our diffuse term
vec3 Diffuse = (LightColor.rgb * LightColor.a) * max(dot(N, L), 0.0);
//pre-multiply ambient color with intensity
vec3 Ambient = AmbientColor.rgb * AmbientColor.a;
//calculate attenuation
float Attenuation = 1.0 / ( Falloff.x + (Falloff.y*D) + (Falloff.z*D*D) );
//the calculation which brings it all together
vec3 Intensity = Ambient + Diffuse * Attenuation;
vec3 FinalColor = DiffuseColor.rgb * Intensity;
gl_FragColor = vColor * vec4(FinalColor, DiffuseColor.a);
}GLSL 分解
现在, 把它分解. 首先, 我们从两个纹理贴图中取样:
//RGBA of our diffuse color
vec4 DiffuseColor = texture2D(u_texture, vTexCoord);
//RGB of our normal map
vec3 NormalMap = texture2D(u_normals, vTexCoord).rgb;接着, 我们需要从当前的片段(译者注:即像素)确定光线向量, 并且纠正它的纵横比例(aspect ratio). 然后在归一化(normalize)之前确定 LightDir 向量的值(长度):
//Delta pos
vec3 LightDir = vec3(LightPos.xy - (gl_FragCoord.xy / Resolution.xy), LightPos.z);
//Correct for aspect ratio
LightDir.x *= Resolution.x / Resolution.y;
//determine magnitude
float D = length(LightDir);在我们的光照模型中, 我们需要从 NormalMap.rgb 中解码 Normal.xyz, 并且归一化我们的向量:
vec3 N = normalize(NormalMap * 2.0 - 1.0);
vec3 L = normalize(LightDir);下一步是计算 Diffuse(漫射) 项. 为了这个, 我们需要使用 LightColor. 在我们的例子中, 我们将会把光线颜色(RGB)和强度(alpha)相乘: LightColor.rgb * LightColor.a. 因此, 所有这些看起来如下:
//Pre-multiply light color with intensity
//Then perform "N dot L" to determine our diffuse term
vec3 Diffuse = (LightColor.rgb * LightColor.a) * max(dot(N, L), 0.0);接着, 我们预相乘(pre-multiply)环境颜色(ambient color)和强度:
vec3 Ambient = AmbientColor.rgb * AmbientColor.a;下一步是用我们的 LightDir的值(前面计算好的)来确定衰减(Attenuation). 统一变量下降系数(Falloff) 定义了我们的常量, 线性和2次方的衰减系数:
float Attenuation = 1.0 / ( Falloff.x + (Falloff.y*D) + (Falloff.z*D*D) );接着, 计算光强度(Intensity)和最终颜色(FinalColor), 并且把它们传递给 gl_FragColor. 注意, 我们机智地保留了 DiffuseColor 的 alpha 值:
vec3 Intensity = Ambient + Diffuse * Attenuation;
vec3 FinalColor = DiffuseColor.rgb * Intensity;
gl_FragColor = vColor * vec4(FinalColor, DiffuseColor.a);抓住你了(Gotchas)
- 在我们的实现中,
LightDir和attenuation依赖于分辨率. 这意味着更改分辨率会影响我们的光的衰减. 根据你的游戏,不同的实现上分辨率无关可能是必需的. - 一个必须处理的常见问题, 关于你游戏的
Y坐标系和你所采用的法线图生成程序(例如CrazyBump)之间的差异. 一些程序允许你导出一个翻转了Y轴的法线图. 下面的图片展示了这个问题:
多光源
实现多光源, 我们只要简单地调整一下算法, 如下:
vec3 Sum = vec3(0.0);
for (... each light ...) {
... calculate light using our illumination model ...
Sum += FinalColor;
}
gl_FragColor = vec4(Sum, DiffuseColor.a);注意, 这样会在你的着色器中引入更多分支(译者注:也就是这个循环), 它会导致性能降低.
这有时被称为"N 照明"(N lighting), 因为我们的系统仅支持一个固定数目 N 的光源. 如果你计划包括大量的光源, 你可能想要调查多个绘制调用(例如 additive blending), 或延迟渲染Deferred shading.
在某个时间点, 你可能会问自己:"为什么我不直接做一个3D游戏?". 比起试着把这些概念应用到 2D 精灵来说, 这是个正当的问题并且可能会带来更好的性能和更少的开发时间.
生成法线图
这里有各种从一张图片生成法线图的方法. 用于转换2D图像为法线图的常用程序和滤镜包括如下:
- SpriteLamp - specifically aimed at 2D normal-map art
- SMAK! - Super Model Army Knife
- CrazyBump
- NVIDIA Texture Tools for Photoshop
- gimp-normalmap
- SSBump Generator
- njob
- ShaderMap
注意, 很多程序都会产生锯齿和错误, 阅读这篇文章How NOT To Make Normal Maps From Photos Or Images来获得更多细节.
你也能使用 3D 建模软件, 如 Blender 或 ZBrush 来精心雕琢出高质量的法线图.
Blender工具
一个工作流的想法是, 生成一个低面数,非常粗糙的 3D 对象在你的艺术资源中. 然后你可以使用这个 Blender Template: Normal Map Pass 把你的对象渲染为一个 2D 正切空间内的法线图. 然后你就能在 PhotoShop 中打开这个法线图并且处理这个漫射(diffuse)颜色图了.
下面是一个 Blender 模板的样子:
进阶阅读
- UpVector - Intro to Shaders & Light
- Bump Mapping Using CG by Søren Dreijer
- Illumination Model Slides
- The Cg Tutorial
- oZone Bump Mapping Tutorial
- Bump Mapping in GLSL - Fabien Sanglard
附录:像素艺术
在创建我的 WebGL 的 法线图像素艺术演示时, 有一堆我不得不考虑的事项. 你可以从这里查看源码和细节.
在这个示例中, 我想让衰减作为一个风格元素变得可见. 典型的做法带来非常平滑的衰减, 它和块状像素艺术风格冲突. 相反, 我使用 cel shading 的光线, 给它一个阶梯状的衰减. 通过片段着色器中的 if-else 语句实现了简单的卡通着色.
下一步的考虑是, 我们希望光线的边缘像素的比例随着精灵(sprites)的像素变化. 实现这个目标的一个方法是通过光照着色器把我们的场景绘制到一个 FBO 中, 然后用一个默认的着色器以一个较大的尺寸把它渲染到屏幕上. 在我们的块状像素艺术中这种照明方式影响整个"纹素"(texels).
其他 APIs
- LibGDX Port
- JS/WebGL Port
- JS/WebGL Port (Pixel Art)