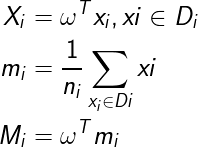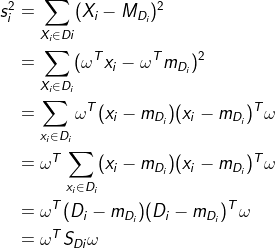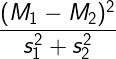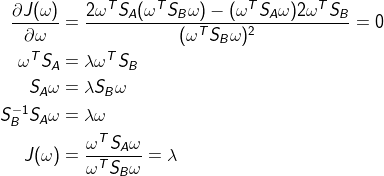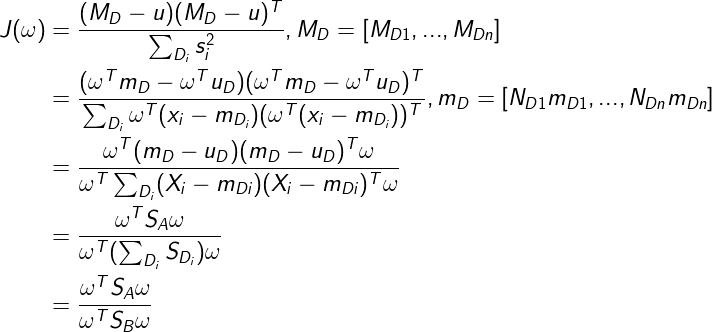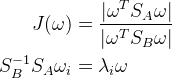之前无标签数据降维PCA,那么像下图带有标签数据,如果用PCA降维将会投影到v轴上,这个投影方差最大,数据将变成不可分状态,LDA将把数据投影加上已有分类这个变量,将数据投影到u轴上
假设原数据分成n类,用矩阵Di表示i类数据,均值向量mi,将设将数据投影到向量w上后,均值分别为Mi,向量w模长为1,则有
矩阵Di投影后类方差为
我们希望 尽可能大,这样数据才能保留之前的分类特性,问题转化为求
的最大值
设
对J求导
J最大值应该是矩阵
例子
from numpy.random import random_sample
import numpy as np
# fig = plt.figure()
N = 600
# 设椭圆中心center
cx = 5
cy = 6
a = 1/8.0
b = 4
X,scale = 2*a*random_sample((N,))+cx-a,60
Y = [2*b*np.sqrt(1.0-((xi-cx)/a)**2)*random_sample()+cy-b*np.sqrt(1.0-((xi-cx)/a)**2) for xi in X]
colors = ['green', 'green']*150
fig, ax = plt.subplots()
fig.set_size_inches(4, 6)
ax.scatter(X, Y,c = "none",s=scale,alpha=1, edgecolors=['green']*N)
X1,scale = 2*a*random_sample((N,))+cx-a,60
Y1 = [2*b*np.sqrt(1.0-((xi-cx)/a)**2)*random_sample()+cy-b*np.sqrt(1.0-((xi-cx)/a)**2) for xi in X1]
ax.scatter(X1+0.3, Y1,c = "none",s=scale,alpha=1, edgecolors=['red']*N)
plt.savefig('lda.png')
plt.show()
自己实现
D1 = np.array([X, Y])
D2 = np.array([X1+0.3, Y1])
m1 = np.mean(D1, axis=1)
m1 = m1[None,]
print m1
m2 = np.mean(D2, axis=1)
m2 = m2[None,]
print m2
SA = np.dot((m1-m2).T,(m1-m2))
S1 = np.dot(D1-m1.T,(D1-m1.T).T)
print S1
S2 = np.dot(D2-m2.T,(D2-m2.T).T)
SB = S1+S2
S = np.dot(np.linalg.inv(SB), SA)
evalue, evec = np.linalg.eig(S)
data1 = np.dot(evec[:,0], D1)
plt.scatter(data1, [0]*data1.size,c = 'g',s=scale,alpha=1, edgecolors=['none']*N)
data2 = np.dot(evec[:,0], D2)
plt.scatter(data2, [0]*data2.size,c = 'r',s=scale,alpha=1, edgecolors=['none']*N)
plt.show()
调用sklearn
from sklearn.lda import LDA
lda = LDA(n_components=1)
X3 = np.column_stack((D1,D2))
print X3.shape
Y = np.ones(X3.shape[1])
print Y.shape
Y[0:N/2]=0
X_trainn_lda = lda.fit_transform(X3.T, Y.T)
print X_trainn_lda.shape
xy = X_trainn_lda.size
plt.scatter(X_trainn_lda, [0]*xy,c = (['g']*(xy/2)+['r']*(xy/2)),s=scale,alpha=1, edgecolors=['none']*N)
plt.show()
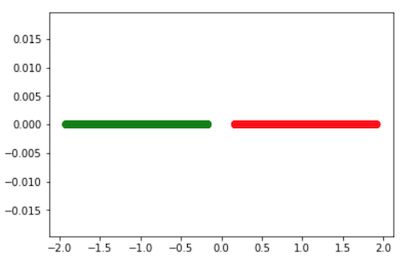
完美投影成两个线段,
多个分组情况
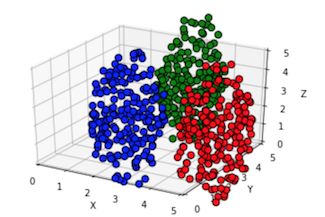
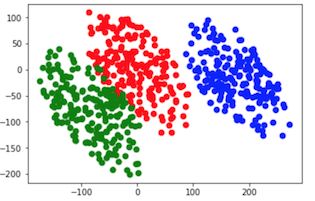
下图是由一个三维空间的三组数据,降维到二维的投影
最后是两个矩阵的比值,这个没有具体的意义,pca知变换后特征值大小代表在该特征向量下投影的离散程度,而特征值的乘积=矩阵行列式,那么
例子
import scipy.io as sio
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from numpy.random import random_sample
import numpy as np
ax=plt.subplot(111,projection='3d') #创建一个三维的绘图工程
N = 200
scale = 60
# 设椭球中心center
cx = 2
cy = 2
cz = 2
a = 1.0
b = 1.5
c = 4.0
def plot(cx,cy,cz, a,b,c,N, color):
X,scale = 2*a*random_sample((N,))+cx-a,60
Y = [b*np.sqrt(1.0-((xi-cx)/a)**2)*(2*random_sample()-1)+cy for xi in X]
Z = [c*np.sqrt(1-((xi-cx)/a)**2-((yi-cy)/b)**2)*(2*random_sample()-1)+cz for xi, yi in zip(X,Y)]
ax.scatter(X, Y, Z,c = color,s=scale,alpha=1, edgecolors=['none']*N)
lr = np.array((X,Y,Z))
return lr
data1 = plot(cx,cy,cz,a,b,c,N, 'b')
data2 = plot(cx+3,cy,cz,a,b,c,N,'r')
data3 = plot(cx,cy+4,cz,a,b,c,N,'g')
data = np.hstack((data1,data2,data3))
print data.shape
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(data)
print X_train_pca.shape
train = np.dot(X_train_pca.T, data)
ax.set_xlim([0,5])
ax.set_ylim([0,5])
ax.set_zlim([0,5])
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
plt.show()
生成三个椭球,数据点红、绿、蓝三组
PCA降维后数据
plt.scatter(train[0,:], train[1,:],c = (['r']*N+['g']*N+['b']*N),s=scale,alpha=1, edgecolors=['none']*N)
plt.show()
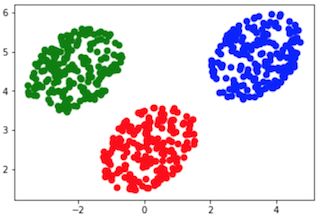
LDA降维后数据
m1 = np.mean(data1, axis=1)[None,].T
m2 = np.mean(data2, axis=1)[None,].T
m3 = np.mean(data3, axis=1)[None,].T
print m1.shape
m = np.hstack((m1,m2,m3))
mTotal = np.mean(data, axis=1)[None,].T
SA = np.dot(m-mTotal, (m-mTotal).T)
SB = np.dot(data1-m1, (data1-m1).T)+np.dot(data2-m2, (data2-m2).T)+np.dot(data3-m3, (data3-m3).T)
S = np.dot(np.linalg.inv(SB), SA)
evalue, evec = np.linalg.eig(S)
myTrain =np.dot(evec, data)
plt.scatter(myTrain[0,:], myTrain[1,:],c = (['r']*N+['g']*N+['b']*N),s=scale,alpha=1, edgecolors=['none']*N)
plt.show()
调用sklearn
from sklearn.lda import LDA
lda = LDA(n_components=2)
y_train =[0]*N+[1]*N+[2]*N
y_train = np.array(y_train)
X_train_lda = lda.fit_transform(data.T, y_train.T)
print X_train_lda.shape
plt.scatter(X_train_lda.T[0,:], X_train_lda.T[1,:],c = (['r']*N+['g']*N+['b']*N),s=scale,alpha=1, edgecolors=['none']*N)
plt.show()