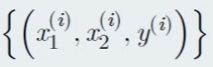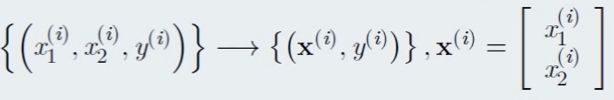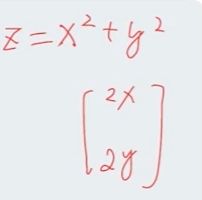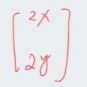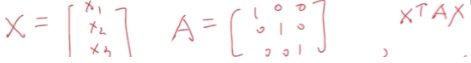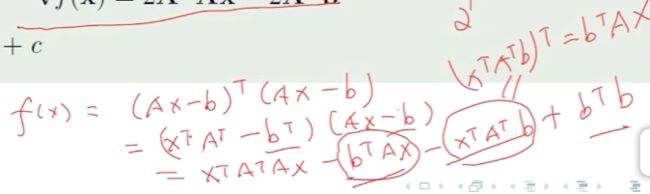线性回归建模
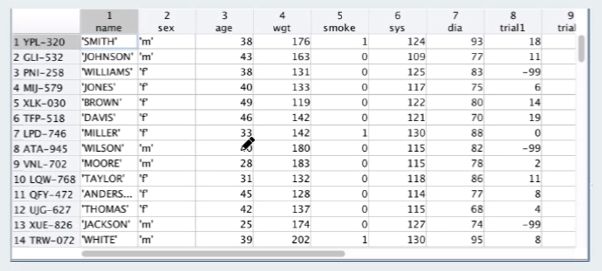
数据集
结构
简述
存在
name - 姓名
sex - 性别
wgt - 体重
smoke - 是否吸烟
预测
sys - 收缩压
建模
训练, 预测
表示一个训练样本, x 表示输入, y 表示输出, 训练数据的 x , y 都是给定的现有数据
则表示训练样本集, 1....N 表示有 N 个样本
当然每个样本可能存在多个特征对结果 y 的影响因素
因此将其简化为 粗体的 X , X 以向量的形式展示, 内部存放多维度的特征值
于此得到的模型为 输入一个 X# , X#内部存在多个特征值, 然后期望获得一个 y# 的预测结果
线性模型
将模型转化成线性模型的方式, 线性模型作为最经典最简单的模型也是最适用的模型
日后当然也可以使用更复杂的模型, 这里线性模型基本上就可以满足我们的要求实现我们的目的
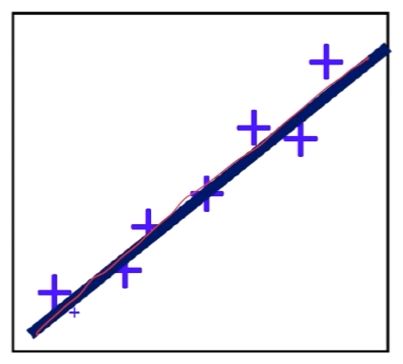
标量的情况, 拟定的线性方程, 使得每一个原始数据 X(i) 的输出 y(i) 的输出近似于真实的 y(i)
ω 是系数, 而 b 为偏置
向量的情况则是这样, 拟定的线性方程, 则是输入的向量进行转置后乘以一个向量 , 既内积
wT 是系数, 而 b 为偏置
最终的结果也是一个标量 , 于此, 这里的问题就是怎么找出这个 ω / wT 以及 b
简单总结
简化为标量线性模型, 转化为向量线性模型, 缺失参数和偏置,
需要怎么样的学习方式才可以得出这个正确的 参数和偏置项, 就是我们要解决的问题
无约束优化分析法
接着上面的建模遇到的问题继续走
本质上这就是个无约束优化问题
所谓的无约束优化问题即是
无约束优化问题
本质上就是一个求极值点的问题
对于代数问题的话即使简单的代入算出即可, 但是对于向量的多维则较为复杂
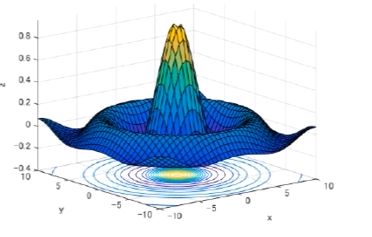
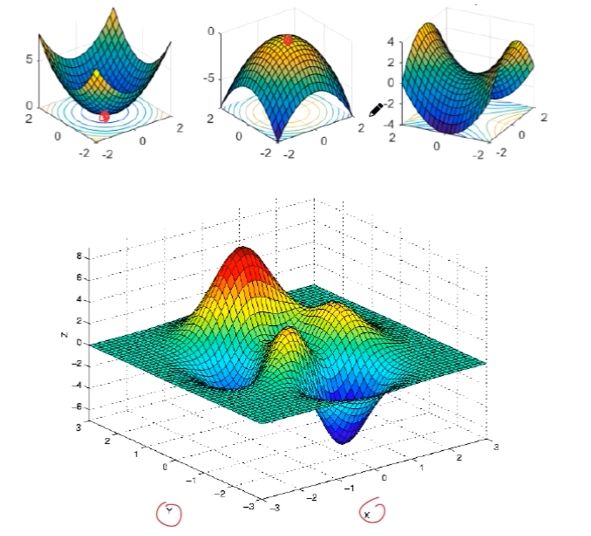
可以使用 Countour 的方法来处理, 如图就是 输入 x, y 得出 z 的图示,
按照每个 z 进行切平面. 下面的环形投影的分析就较为方便
但是超多维度的时候的处理会更为复杂, 因此只能在代数上解决此类问题, 而可视化是很难的体现
极值点的情况当然也很多, 可以局部可以全局, 因此延续上面的问题转变成了求极值问题
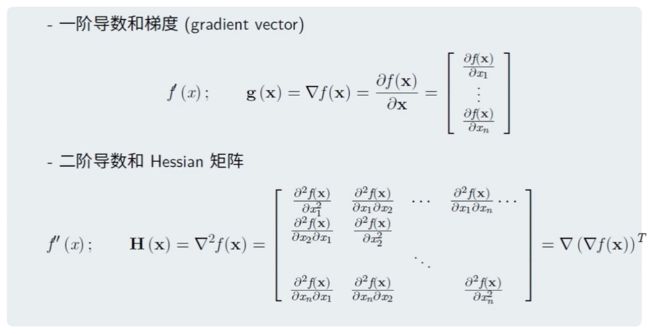
梯度和Hessian 矩阵
既然是求某一个形状的方程式, 那就需要计算的它的扭曲方式或者射出方位,
这需要用到导数, 导数本质上就是求切线, 速度等定义, 这样就可以计算出他的形状
因此引入梯度的概念
一阶导数和梯度的一个简单的举例,
输入的是两维的, 输出的也是两维的向量
大部分情况 用
来表示梯度,. 为了简单更喜欢用 g(x) 来表示梯度
二阶导数既在一阶求导后再求导,
例如 x2 -> 2x -> 2
如果是向量的话, 二阶导数就会成为 海森矩阵
本质上 海森矩阵是个对称矩阵
基于上面的 z = x2 + y2 的例子
一阶导数的结果是
再进行二次求导的结果就是
海森矩阵一般写成 H(x) 的形式
二次型
仅仅这些还不够要用到二次型
二次型的例子:
这里根据定义即可发现, 对于所有的对称矩阵都可以判定正(定矩阵)负(定矩阵)
而且正负矩阵也对特征进行了明确
因此前面说的 海森矩阵本身作为对称矩阵既可以进行正负的判定
具体计算
在有了上面的前提下才可以进行计算
具体的计算
最终的梯度结果即是个二次型
泰勒级数
得到了梯度后, 进行函数的分析,这时候需要用到泰勒展开
既可以看出 , 一阶导数就是梯度, 二阶导数就是 海森矩阵的那那个二次型
当然还有三阶导数四阶导数等等, 但是对于这里的使用已经足够了. 二阶足以
无约束迭代法
线性回归求解