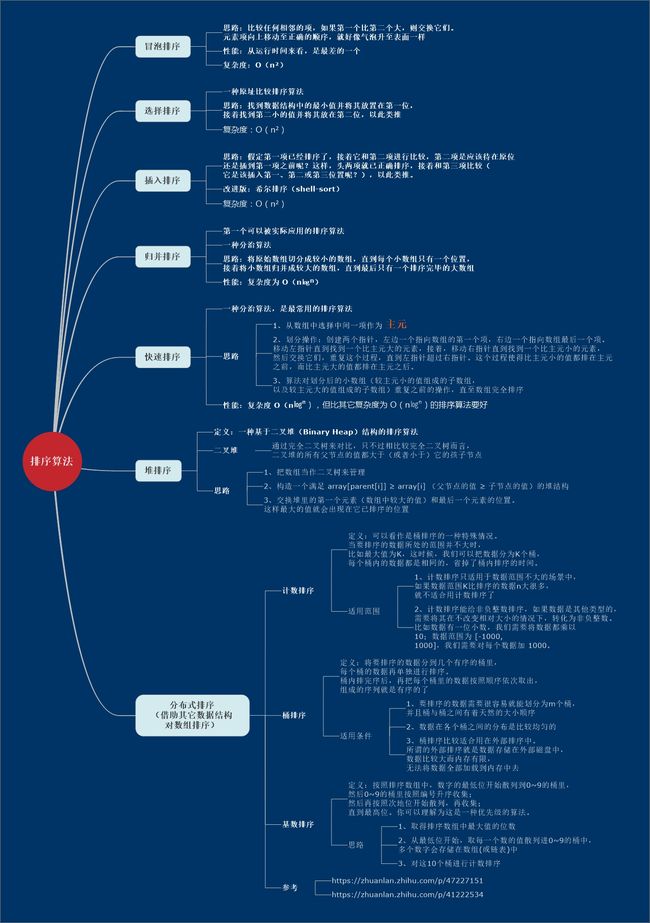
本章将介绍 JavaScript 如何实现排序,几种排序算法介绍如下图:
准备工具函数 util.js 备用:
export const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1,
EQUALS: 0
};
export const DOES_NOT_EXIST = -1;
export function lesserEquals(a, b, compareFn) {
const comp = compareFn(a, b);
return comp === Compare.LESS_THAN || comp === Compare.EQUALS;
}
export function biggerEquals(a, b, compareFn) {
const comp = compareFn(a, b);
return comp === Compare.BIGGER_THAN || comp === Compare.EQUALS;
}
export function defaultCompare(a, b) {
if (a === b) {
return Compare.EQUALS;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
export function defaultEquals(a, b) {
return a === b;
}
export function defaultToString(item) {
if (item === null) {
return 'NULL';
} if (item === undefined) {
return 'UNDEFINED';
} if (typeof item === 'string' || item instanceof String) {
return `${item}`;
}
return item.toString();
}
export function swap(array, a, b) {
[array[a], array[b]] = [array[b], array[a]];
}
export function reverseCompare(compareFn) {
return (a, b) => compareFn(b, a);
}
export function defaultDiff(a, b) {
return Number(a) - Number(b);
}
借助 算法可视化工具 来直观感受各算法的实现思路。
各排序算法实现视频集成演示
下面介绍一下各排序算法的实现思路、代码实现以及动画演示:
1、冒泡排序
基本思路:比较任何相邻的项,如果第一个比第二个大,则交换它们。元素项向上移动至正确的顺序,就好像气泡升至表面一样。
代码实现:
import { Compare, defaultCompare, swap } from '../util';
export function bubbleSort(array, compareFn = defaultCompare) {
const { length } = array;
for (let i = 0; i < length; i++) {
for (let j = 0; j < length - 1; j++) {
// 比较任何相邻的项,如果第一个比第二个大,则交换它们
if (compareFn(array[j], array[j + 1]) === Compare.BIGGER_THAN) {
swap(array, j, j + 1);
}
}
}
return array;
}
上面的冒泡排序性能并不是最好的,还可以优化如下:
import { Compare, defaultCompare, swap } from '../util';
export function bubbleSort(array, compareFn = defaultCompare) {
const { length } = array;
for (let i = 0; i < length; i++) {
// 区别在这:从内循环减去外循环已跑过的轮数,就可以避免内循环中所有不必要的比较
for (let j = 0; j < length - 1 - i; j++) {
// 比较任何相邻的项,如果第一个比第二个大,则交换它们
if (compareFn(array[j], array[j + 1]) === Compare.BIGGER_THAN) {
swap(array, j, j + 1);
}
}
}
return array;
}
2、选择排序
基本思路:找到数据结构中的最小值并将其放置在第一位,接着找到第二小的值并将其放在第二位,以此类推。
代码实现:
import { Compare, defaultCompare, swap } from '../../util';
export const selectionSort = (array, compareFn = defaultCompare) => {
const { length } = array;
let indexMin;
for (let i = 0; i < length - 1; i++) {
indexMin = i;
for (let j = i; j < length; j++) {
if (compareFn(array[indexMin], array[j]) === Compare.BIGGER_THAN) {
indexMin = j;
}
}
if (i !== indexMin) {
swap(array, i, indexMin);
}
}
return array;
};
3、插入排序
基本思路:假定第一项已经排序了,接着它和第二项进行比较,第二项是应该待在原位还是插到第一项之前呢?这样,头两项就已正确排序,接着和第三项比较(它是该插入第一、第二或第三位置呢?),以此类推。
代码实现:
import { Compare, defaultCompare } from '../../util';
export const insertionSort = (array, compareFn = defaultCompare) => {
const { length } = array;
let temp;
for (let i = 1; i < length; i++) {
let j = i;
temp = array[i];
while (j > 0 && compareFn(array[j - 1], temp) === Compare.BIGGER_THAN) {
array[j] = array[j - 1];
j--;
}
array[j] = temp;
}
return array;
};
这种插入排序的性能并不是最好的,在 1959 年 D.L.Shell 提出了更高效的插入排序:希尔排序。
基本思路:把数列进行分组(不停使用插入排序),直至从宏观上看起来有序,最后插入排序起来就容易了(无须多次移位或交换)。
代码实现:
import { Compare, defaultCompare } from '../../util';
export function shellSort(array, compareFn = defaultCompare) {
// 定义间隔序列
let increment = array.length / 2;
while (increment > 0) {
for (let i = increment; i < array.length; i++) {
let j = i;
const temp = array[i];
while (j >= increment && compareFn(array[j - increment], temp) === Compare.BIGGER_THAN) {
array[j] = array[j - increment];
j -= increment;
}
array[j] = temp;
}
if (increment === 2) {
increment = 1;
} else {
increment = Math.floor((increment * 5) / 11);
}
}
return array;
}
4、归并排序
基本思路:将原始数组切分成较小的数组,直到每个小数组只有一个位置,接着将小数组归并成较大的数组,直到最后只有一个排序完毕的大数组。
代码实现:
import { Compare, defaultCompare } from '../../util';
function merge(left, right, compareFn) {
let i = 0;
let j = 0;
const result = [];
// 将原始数组切分成较小的数组,直到每个小数组只有一个位置
while (i < left.length && j < right.length) {
result.push(compareFn(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++]);
}
return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}
export function mergeSort(array, compareFn = defaultCompare) {
if (array.length > 1) {
const { length } = array;
const middle = Math.floor(length / 2);
const left = mergeSort(array.slice(0, middle), compareFn);
const right = mergeSort(array.slice(middle, length), compareFn);
// 将小数组归并成较大的数组,直到最后只有一个排序完毕的大数组
array = merge(left, right, compareFn);
}
return array;
}
5、快速排序
基本思路:
- 从数组中选择中间一项作为 主元
- 划分操作:创建两个指针,左边一个指向数组的第一个项,右边一个指向数组最后一个项。移动左指针直到找到一个比主元大的元素,接着,移动右指针直到找到一个比主元小的元素,然后交换它们,重复这个过程,直到左指针超过右指针。这个过程使得比主元小的值都排在主元之前,而比主元大的值都排在主元之后
- 算法对划分后的小数组(较主元小的值组成的子数组,以及较主元大的值组成的子数组)重复之前的操作,直至数组完全排序
代码实现:
import { Compare, defaultCompare, swap } from '../../util';
function partition(array, left, right, compareFn) {
// 从数组中选择中间一项作为主元 pivot
const pivot = array[Math.floor((right + left) / 2)];
// 定义左右指针
let i = left;
let j = right;
while (i <= j) {
// 移动左指针直到找到一个比主元大的元素
while (compareFn(array[i], pivot) === Compare.LESS_THAN) {
i++;
}
// 移动右指针直到找到一个比主元小的元素
while (compareFn(array[j], pivot) === Compare.BIGGER_THAN) {
j--;
}
if (i <= j) {
swap(array, i, j);
i++;
j--;
}
}
return i;
}
function quick(array, left, right, compareFn) {
let index;
if (array.length > 1) {
index = partition(array, left, right, compareFn);
if (left < index - 1) {
quick(array, left, index - 1, compareFn);
}
if (index < right) {
quick(array, index, right, compareFn);
}
}
return array;
}
export function quickSort(array, compareFn = defaultCompare) {
return quick(array, 0, array.length - 1, compareFn);
}
6、堆排序
基本思路:
- 把数组当作二叉树来管理
- 构造一个满足 array[parent[i]] ≥ array[i] (父节点的值 ≥ 子节点的值)的堆结构
- 交换堆里的第一个元素(数组中较大的值)和最后一个元素的位置。这样最大的值就会出现在它已排序的位置
代码实现:
import { defaultCompare, swap } from '../../util';
// 把数组当作二叉树来管理
function heapify(array, index, heapSize, compareFn) {
let largest = index;
const left = (2 * index) + 1;
const right = (2 * index) + 2;
if (left < heapSize && compareFn(array[left], array[index]) > 0) {
largest = left;
}
if (right < heapSize && compareFn(array[right], array[largest]) > 0) {
largest = right;
}
if (largest !== index) {
swap(array, index, largest);
heapify(array, largest, heapSize, compareFn);
}
}
// 构造一个满足 array[parent[i]] ≥ array[i] (父节点的值 ≥ 子节点的值)的堆结构
function buildMaxHeap(array, compareFn) {
for (let i = Math.floor(array.length / 2); i >= 0; i -= 1) {
heapify(array, i, array.length, compareFn);
}
return array;
}
export default function heapSort(array, compareFn = defaultCompare) {
let heapSize = array.length;
buildMaxHeap(array, compareFn);
while (heapSize > 1) {
swap(array, 0, --heapSize);
heapify(array, 0, heapSize, compareFn);
}
return array;
}
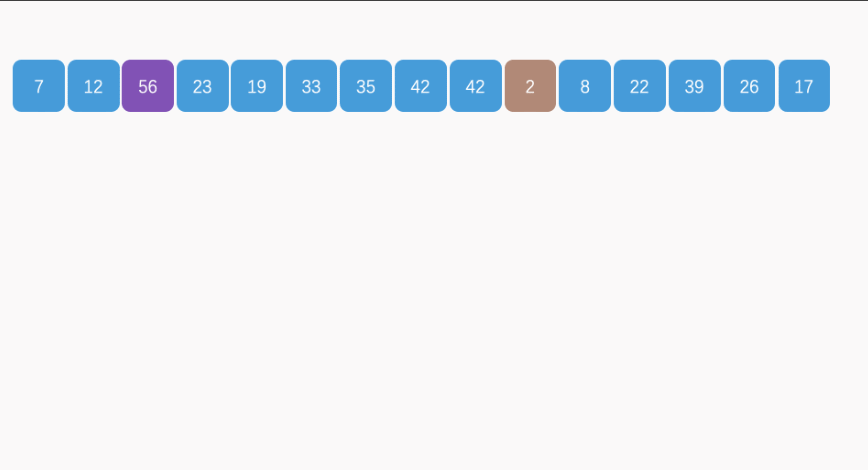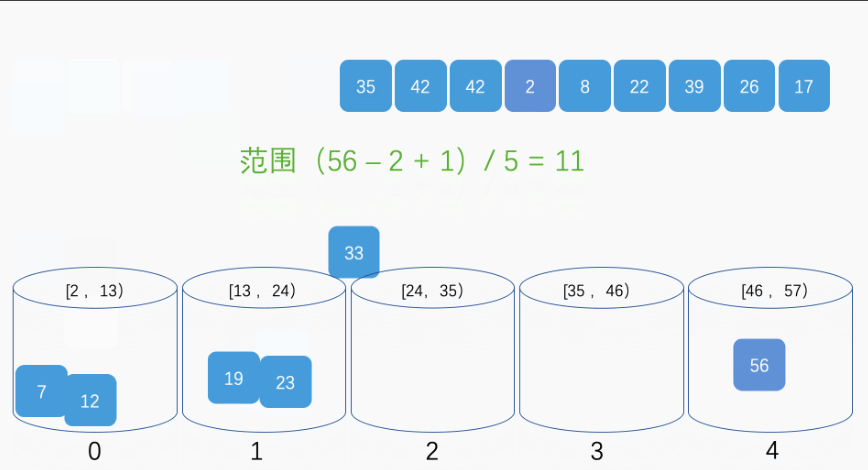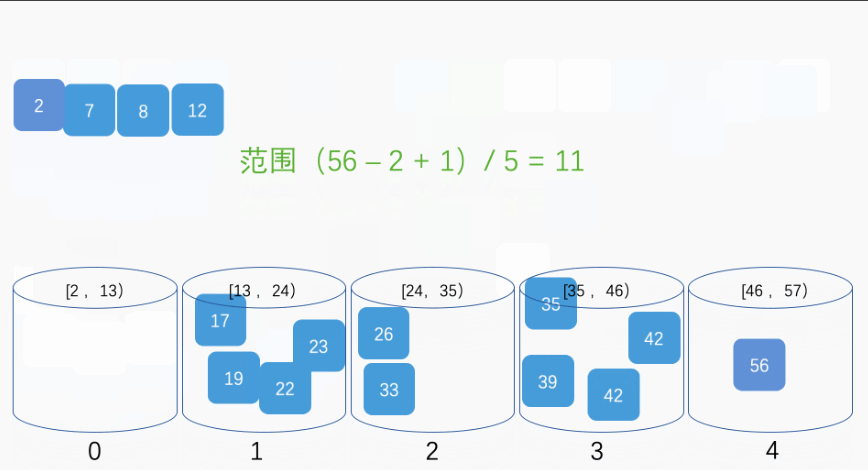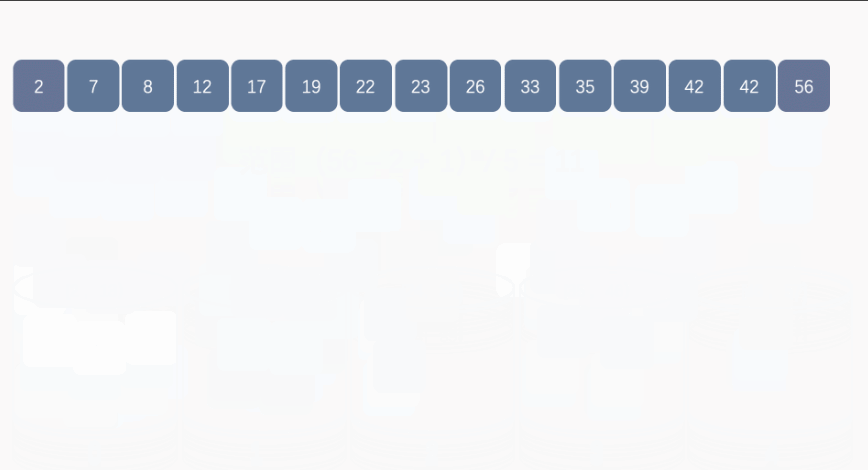
7、桶排序
基本思路:将要排序的数据分到几个有序的桶里,每个桶的数据再单独进行排序。桶内排完序后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
代码实现:
// 借用插入排序
import { insertionSort } from './insertion-sort';
// 创建桶
function createBuckets(array, bucketSize) {
let minValue = array[0];
let maxValue = array[0];
for (let i = 1; i < array.length; i++) {
if (array[i] < minValue) {
minValue = array[i];
} else if (array[i] > maxValue) {
maxValue = array[i];
}
}
// 桶的数量确定
const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
const buckets = [];
for (let i = 0; i < bucketCount; i++) {
buckets[i] = [];
}
for (let i = 0; i < array.length; i++) {
buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]);
}
return buckets;
}
function sortBuckets(buckets) {
const sortedArray = [];
for (let i = 0; i < buckets.length; i++) {
if (buckets[i] != null) {
insertionSort(buckets[i]);
sortedArray.push(...buckets[i]);
}
}
return sortedArray;
}
export function bucketSort(array, bucketSize = 5) {
if (array.length < 2) {
return array;
}
const buckets = createBuckets(array, bucketSize);
return sortBuckets(buckets);
}
桶排序使用条件:
- 要排序的数据需要很容易就能划分为 bucketCount 个桶,并且桶与桶之间有着天然的大小顺序
- 数据在各个桶之间的分布是比较均匀的
- 桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据比较大而内存有限,无法将数据全部加载到内存中去
8、计数排序
基本思路:可以看作是桶排序的一种特殊情况。当要排序的数据所处的范围并不大时,比如最大值为 K,这时候,我们可以把数据分为 K 个桶,每个桶内的数据都是相同的,省掉了桶内排序的时间。
代码实现:
import { defaultCompare, Compare } from '../../util';
function findMaxValue(array, compareFn = defaultCompare) {
if (array && array.length > 0) {
let max = array[0];
for (let i = 1; i < array.length; i++) {
if (compareFn(max, array[i]) === Compare.LESS_THAN) {
max = array[i];
}
}
return max;
}
return undefined;
}
export function countingSort(array) {
if (array.length < 2) {
return array;
}
const maxValue = findMaxValue(array);
let sortedIndex = 0;
const counts = new Array(maxValue + 1);
array.forEach(element => {
if (!counts[element]) {
counts[element] = 0;
}
counts[element]++;
});
// console.log('Frequencies: ' + counts.join());
counts.forEach((element, i) => {
while (element > 0) {
array[sortedIndex++] = i;
element--;
}
});
return array;
}
适用条件:
- 计数排序只适用于数据范围不大的场景中,如果数据范围K比排序的数据n大很多,就不适合用计数排序了
- 计数排序能给非负整数排序,如果数据是其他类型的,需要将其在不改变相对大小的情况下,转化为非负整数。比如数据有一位小数,我们需要将数据都乘以 10;数据范围为 [-1000, 1000],我们需要对每个数据加 1000
9、基数排序
基本思路:按照排序数组中,数字的最低位开始散列到 0-9 的桶里,然后 0-9的桶里按照编号升序收集;然后再按照次地位开始散列,再收集;直到最高位。你可以理解为这是一种优先级的算法。
代码实现:
import { defaultCompare, Compare } from '../../util';
function findMaxValue(array, compareFn = defaultCompare) {
if (array && array.length > 0) {
let max = array[0];
for (let i = 1; i < array.length; i++) {
if (compareFn(max, array[i]) === Compare.LESS_THAN) {
max = array[i];
}
}
return max;
}
return undefined;
}
function findMinValue(array, compareFn = defaultCompare) {
if (array && array.length > 0) {
let min = array[0];
for (let i = 1; i < array.length; i++) {
if (compareFn(min, array[i]) === Compare.BIGGER_THAN) {
min = array[i];
}
}
return min;
}
return undefined;
}
const getBucketIndex = (value, minValue, significantDigit, radixBase) =>
Math.floor(((value - minValue) / significantDigit) % radixBase);
const countingSortForRadix = (array, radixBase, significantDigit, minValue) => {
let bucketsIndex;
const buckets = [];
const aux = [];
for (let i = 0; i < radixBase; i++) {
buckets[i] = 0;
}
for (let i = 0; i < array.length; i++) {
bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase);
buckets[bucketsIndex]++;
}
for (let i = 1; i < radixBase; i++) {
buckets[i] += buckets[i - 1];
}
for (let i = array.length - 1; i >= 0; i--) {
bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase);
aux[--buckets[bucketsIndex]] = array[i];
}
for (let i = 0; i < array.length; i++) {
array[i] = aux[i];
}
return array;
};
export function radixSort(array, radixBase = 10) {
if (array.length < 2) {
return array;
}
const minValue = findMinValue(array);
const maxValue = findMaxValue(array);
// Perform counting sort for each significant digit, starting at 1
let significantDigit = 1;
while ((maxValue - minValue) / significantDigit >= 1) {
// console.log('radix sort for digit ' + significantDigit);
array = countingSortForRadix(array, radixBase, significantDigit, minValue);
// console.log(array.join());
significantDigit *= radixBase;
}
return array;
}
适用条件:
- 取得排序数组中最大值的位数
- 从最低位开始,取每一个数的值散列进0~9的桶中,多个数字会存储在数组(或链表)中
- 对这10个桶进行计数排序
10、各算法之间的复杂度对比
关于时间复杂度:
- 平方阶 (O(n2)) 排序 各类简单排序:直接插入、直接选择和冒泡排序
- 线性对数阶 (O(nlog2n)) 排序:快速排序、堆排序和归并排序
- O(n1+§)) 排序,§ 是介于 0 和 1 之间的常数: 希尔排序
- 线性阶 (O(n)) 排序:基数排序,此外还有桶、箱排序
关于稳定性:
- 稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序
- 不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序