3.线性神经网络 - 随机梯度下降法

随机梯度下降法:stochastic gradient descent

大纲

1. look --- 大数据情况遇到什么问题

2. write --- 随机梯度下降法

3. code --- python

---

Large scale 带来的问题

每次更新权值都要计算所有的数据点，才能进行一次更新
数据量大的情况下，性能会很差

stochastic gradient descent

随机梯度下降算法，相比批量梯度下降，它每读到一个数据点，都会进行一次权值更新

• 好处：快，几十万的数据有可能在第几千个的时候就会收敛
• 坏处：因为是每个数据点都会更新权值，呢些离群点会对算法影响很大，算法噪声大

解决方法

1. 利用洗牌算法，每次迭代都用随机序列防止循环
2. 自适应的学习率，a / (b + number of iteration)，a,b是常数，比固定的学习率有更大的机会达到最小误差的收敛点

随机梯度下降算法

由图可见，由于是每个点都进行权值更新，在算法初期收敛速度很快，又因为是自适应的学习率，越接近最小无差点，逼近速度越慢

误差收敛图

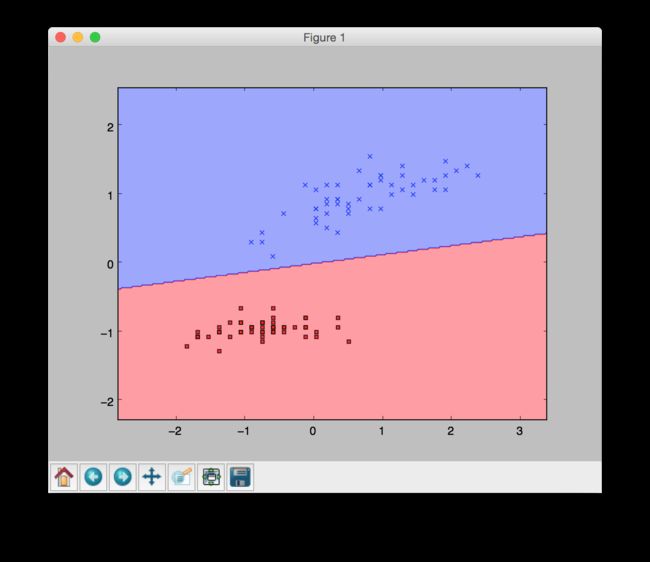
根据计算得到的分类平面如图

分类平面示意图

随机梯度很适合在线学习，因为它不需要所有的训练点就可以进行模型训练。同时更加节约内存

Code！！！

from numpy.random import seed
class AdalineSGD(object):

    # --------  参数  --------#
    # 参数1   eta:float   学习率
    # 参数2   n_iter:int  循环次数
    # --------  属性  --------#
    # 属性1   w_:1d_array         拟合后权值
    # 属性2   errors_:list        每次迭代的错误分类
    # 属性3   shuffles:bool       每次迭代时候打乱顺序
    # 属性4   random_state:int    设置循环状态,初始化权值

    # 初始化
    def __init__(self,eta=0.01,n_iter=10,shuffle=True,random_state=None):
        self.eta = eta
        self.n_iter = n_iter
        self.shuffle = shuffle
        self.w_initialized = False
        if(random_state):
            seed(random_state)

    # 训练模型
    def fit(self,X,y):
        self._initialize_weights(X.shape[1])
        self.cost_ = []
        for i in range(self.n_iter):
            if(self.shuffle):
                X,y = self._shuffle(X,y)
            cost = []
            for xi ,target in zip(X,y):
                cost.append(self._update_weights(xi,target))
            avg_cost = sum(cost)/len(y)
            self.cost_.append(avg_cost)
        return self

    # 不初始化权值进行对训练数据进行拟合
    def partial_fit(self,X,y):
        if not self.w_initialized:
            self._initialize_weights(X.shape[1])
        if y.ravel().shapr[0] > 1:
            for xi,target in zip(X,y):
                self._update_weights(xi,target)
        else:
            self._update_weights(X,y)
        return self

    # 输入和权值的点积,即公式的z函数,图中的net_input
    def net_input(self,X):
        return np.dot(X,self.w_[1:]) + self.w_[0]

    # 线性激活函数
    def activation(self,X):
        return self.net_input(X)

    # 利用阶跃函数返回分类标签
    def predict(self,X):
        return np.where(self.activation(X)>=0.0,1,-1)

    # 对数据进行随机打乱
    def _shuffle(self,X,y):
        r = np.random.permutation(len(y)) # 随机索引值
        return X[r],y[r]

    # 初始化权值向量
    def _initialize_weights(self,m):
        self.w_ = np.zeros(1+m)
        self.w_initialized = True

    # 应用自适应线性神经网络更新权值
    def _update_weights(self,xi,target):
        output = self.net_input(xi)
        error = (target-output)
        self.w_[1:] += self.eta * xi.dot(error)
        self.w_[0] += self.eta * error
        cost = 0.5 * error ** 2
        return cost