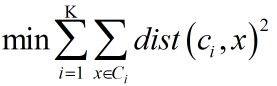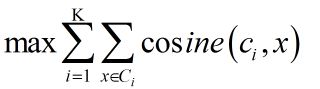基本Kmeans算法介绍及其实现

原文：http://blog.csdn.net/liuheng0111/article/details/52149040

1.基本Kmeans算法[1]

选择K个点作为初始质心
repeat
    将每个点指派到最近的质心，形成K个簇
    重新计算每个簇的质心
until 簇不发生变化或达到最大迭代次数

时间复杂度：O(tKmn)，其中，t为迭代次数，K为簇的数目，m为记录数，n为维数

空间复杂度：O((m+K)n)，其中，K为簇的数目，m为记录数，n为维数

2.注意问题

（1）K如何确定

        kmenas算法首先选择K个初始质心，其中K是用户指定的参数，即所期望的簇的个数。这样做的前提是我们已经知道数据集中包含多少个簇，但很多情况下，我们并不知道数据的分布情况，实际上聚类就是我们发现数据分布的一种手段，这就陷入了鸡和蛋的矛盾。如何有效的确定K值，这里大致提供几种方法，若各位有更好的方法，欢迎探讨。

1.与层次聚类结合[2]

         经常会产生较好的聚类结果的一个有趣策略是，首先采用层次凝聚算法决定结果粗的数目，并找到一个初始聚类，然后用迭代重定位来改进该聚类。

2.稳定性方法[3]

        稳定性方法对一个数据集进行2次重采样产生2个数据子集，再用相同的聚类算法对2个数据子集进行聚类，产生2个具有k个聚类的聚类结果，计算2个聚类结果的相似度的分布情况。2个聚类结果具有高的相似度说明k个聚类反映了稳定的聚类结构，其相似度可以用来估计聚类个数。采用次方法试探多个k，找到合适的k值。

3.系统演化方法[3]

         系统演化方法将一个数据集视为伪热力学系统，当数据集被划分为K个聚类时称系统处于状态K。系统由初始状态K=1出发，经过分裂过程和合并过程，系统将演化到它的稳定平衡状态Ki，其所对应的聚类结构决定了最优类数Ki。系统演化方法能提供关于所有聚类之间的相对边界距离或可分程度，它适用于明显分离的聚类结构和轻微重叠的聚类结构。

4.使用canopy算法进行初始划分[4]

          基于Canopy Method的聚类算法将聚类过程分为两个阶段
         Stage1、聚类最耗费计算的地方是计算对象相似性的时候，Canopy Method在第一阶段选择简单、计算代价较低的方法计算对象相似性，将相似的对象放在一个子集中，这个子集被叫做Canopy ，通过一系列计算得到若干Canopy，Canopy之间可以是重叠的，但不会存在某个对象不属于任何Canopy的情况，可以把这一阶段看做数据预处理；
          Stage2、在各个Canopy 内使用传统的聚类方法(如K-means)，不属于同一Canopy 的对象之间不进行相似性计算。
从这个方法起码可以看出两点好处：首先，Canopy 不要太大且Canopy 之间重叠的不要太多的话会大大减少后续需要计算相似性的对象的个数；其次，类似于K-means这样的聚类方法是需要人为指出K的值的，通过Stage1得到的Canopy 个数完全可以作为这个K值，一定程度上减少了选择K的盲目性。

         其他方法如贝叶斯信息准则方法（BIC）可参看文献[5]。

（2）初始质心的选取

          选择适当的初始质心是基本kmeans算法的关键步骤。常见的方法是随机的选取初始质心，但是这样簇的质量常常很差。处理选取初始质心问题的一种常用技术是：多次运行，每次使用一组不同的随机初始质心，然后选取具有最小SSE（误差的平方和）的簇集。这种策略简单，但是效果可能不好，这取决于数据集和寻找的簇的个数。

          第二种有效的方法是，取一个样本，并使用层次聚类技术对它聚类。从层次聚类中提取K个簇，并用这些簇的质心作为初始质心。该方法通常很有效，但仅对下列情况有效：（1）样本相对较小，例如数百到数千（层次聚类开销较大）；（2）K相对于样本大小较小

           第三种选择初始质心的方法，随机地选择第一个点，或取所有点的质心作为第一个点。然后，对于每个后继初始质心，选择离已经选取过的初始质心最远的点。使用这种方法，确保了选择的初始质心不仅是随机的，而且是散开的。但是，这种方法可能选中离群点。此外，求离当前初始质心集最远的点开销也非常大。为了克服这个问题，通常该方法用于点样本。由于离群点很少（多了就不是离群点了），它们多半不会在随机样本中出现。计算量也大幅减少。

          第四种方法就是上面提到的canopy算法。

（3）距离的度量

          常用的距离度量方法包括：欧几里得距离和余弦相似度。两者都是评定个体间差异的大小的。欧几里得距离度量会受指标不同单位刻度的影响，所以一般需要先进行标准化，同时距离越大，个体间差异越大；空间向量余弦夹角的相似度度量不会受指标刻度的影响，余弦值落于区间[-1,1]，值越大，差异越小。但是针对具体应用，什么情况下使用欧氏距离，什么情况下使用余弦相似度？

          从几何意义上来说，n维向量空间的一条线段作为底边和原点组成的三角形，其顶角大小是不确定的。也就是说对于两条空间向量，即使两点距离一定，他们的夹角余弦值也可以随意变化。感性的认识，当两用户评分趋势一致时，但是评分值差距很大，余弦相似度倾向给出更优解。举个极端的例子，两用户只对两件商品评分，向量分别为(3,3)和(5,5)，这两位用户的认知其实是一样的，但是欧式距离给出的解显然没有余弦值合理。[6]

（4）质心的计算

         对于距离度量不管是采用欧式距离还是采用余弦相似度，簇的质心都是其均值，即向量各维取平均即可。对于距离对量采用其它方式时，这个还没研究过。

（5）算法停止条件

         一般是目标函数达到最优或者达到最大的迭代次数即可终止。对于不同的距离度量，目标函数往往不同。当采用欧式距离时，目标函数一般为最小化对象到其簇质心的距离的平方和，如下：

         当采用余弦相似度时，目标函数一般为最大化对象到其簇质心的余弦相似度和，如下：

（6）空聚类的处理

           如果所有的点在指派步骤都未分配到某个簇，就会得到空簇。如果这种情况发生，则需要某种策略来选择一个替补质心，否则的话，平方误差将会偏大。一种方法是选择一个距离当前任何质心最远的点。这将消除当前对总平方误差影响最大的点。另一种方法是从具有最大SSE的簇中选择一个替补的质心。这将分裂簇并降低聚类的总SSE。如果有多个空簇，则该过程重复多次。另外，编程实现时，要注意空簇可能导致的程序bug。

3.适用范围及缺陷

           Kmenas算法试图找到使平凡误差准则函数最小的簇。当潜在的簇形状是凸面的，簇与簇之间区别较明显，且簇大小相近时，其聚类结果较理想。前面提到，该算法时间复杂度为O(tKmn)，与样本数量线性相关，所以，对于处理大数据集合，该算法非常高效，且伸缩性较好。但该算法除了要事先确定簇数K和对初始聚类中心敏感外，经常以局部最优结束，同时对“噪声”和孤立点敏感，并且该方法不适于发现非凸面形状的簇或大小差别很大的簇。

4.实现

#include
#include
#include
#include
#include
#include
#define k 3//簇的数目
using namespace std;
//存放元组的属性信息
typedef vector Tuple;//存储每条数据记录

int dataNum;//数据集中数据记录数目
int dimNum;//每条记录的维数

//计算两个元组间的欧几里距离
double getDistXY(const Tuple& t1, const Tuple& t2)
{
    double sum = 0;
    for(int i=1; i<=dimNum; ++i)
    {
        sum += (t1[i]-t2[i]) * (t1[i]-t2[i]);
    }
    return sqrt(sum);
}

//根据质心，决定当前元组属于哪个簇
int clusterOfTuple(Tuple means[],const Tuple& tuple){
    double dist=getDistXY(means[0],tuple);
    double tmp;
    int label=0;//标示属于哪一个簇
    for(int i=1;i
        tmp=getDistXY(means[i],tuple);
        if(tmp
    }
    return label;
}
//获得给定簇集的平方误差
double getVar(vector clusters[],Tuple means[]){
    double var = 0;
    for (int i = 0; i < k; i++)
    {
        vector t = clusters[i];
        for (int j = 0; j< t.size(); j++)
        {
            var += getDistXY(t[j],means[i]);
        }
    }
    //cout<<"sum:"<
    return var;

}
//获得当前簇的均值（质心）
Tuple getMeans(const vector& cluster){

    int num = cluster.size();
    Tuple t(dimNum+1, 0);
    for (int i = 0; i < num; i++)
    {
        for(int j=1; j<=dimNum; ++j)
        {
            t[j] += cluster[i][j];
        }
    }
    for(int j=1; j<=dimNum; ++j)
        t[j] /= num;
    return t;
    //cout<<"sum:"<
}

void print(const vector clusters[])
{
    for(int lable=0; lable
    {
        cout<<"第"<
        vector t = clusters[lable];
        for(int i=0; i
        {
            cout<
            for(int j=0; j<=dimNum; ++j)
            {
                cout<
            }
            cout<<")\n";
        }
    }
}

void KMeans(vector& tuples){
    vector clusters[k];//k个簇
    Tuple means[k];//k个中心点
    int i=0;
    //一开始随机选取k条记录的值作为k个簇的质心（均值）
    srand((unsigned int)time(NULL));
    for(i=0;i
        int iToSelect = rand()%tuples.size();
        if(means[iToSelect].size() == 0)
        {
            for(int j=0; j<=dimNum; ++j)
            {
                means[i].push_back(tuples[iToSelect][j]);
            }
            ++i;
        }
    }
    int lable=0;
    //根据默认的质心给簇赋值
    for(i=0;i!=tuples.size();++i){
        lable=clusterOfTuple(means,tuples[i]);
        clusters[lable].push_back(tuples[i]);
    }
    double oldVar=-1;
    double newVar=getVar(clusters,means);
    cout<<"初始的的整体误差平方和为："<
    int t = 0;
    while(abs(newVar - oldVar) >= 1) //当新旧函数值相差不到1即准则函数值不发生明显变化时，算法终止
    {
        cout<<"第 "<<++t<<" 次迭代开始："<
        for (i = 0; i < k; i++) //更新每个簇的中心点
        {
            means[i] = getMeans(clusters[i]);
        }
        oldVar = newVar;
        newVar = getVar(clusters,means); //计算新的准则函数值
        for (i = 0; i < k; i++) //清空每个簇
        {
            clusters[i].clear();
        }
        //根据新的质心获得新的簇
        for(i=0; i!=tuples.size(); ++i){
            lable=clusterOfTuple(means,tuples[i]);
            clusters[lable].push_back(tuples[i]);
        }
        cout<<"此次迭代之后的整体误差平方和为："<
    }

    cout<<"The result is:\n";
    print(clusters);
}
int main(){

    char fname[256];
    cout<<"请输入存放数据的文件名： ";
    cin>>fname;
    cout<
    cout<
    cin>>dimNum;
    cout<
    cin>>dataNum;
    ifstream infile(fname);
    if(!infile){
        cout<<"不能打开输入的文件"<
        return 0;
    }
    vector tuples;
    //从文件流中读入数据
    for(int i=0; i
    {
        string str;
        getline(infile, str);
        istringstream istr(str);
        Tuple tuple(dimNum+1, 0);//第一个位置存放记录编号，第2到dimNum+1个位置存放实际元素
        tuple[0] = i+1;
        for(int j=1; j<=dimNum; ++j)
        {
            istr>>tuple[j];
        }
        tuples.push_back(tuple);
    }

    cout<
    KMeans(tuples);
    return 0;
}

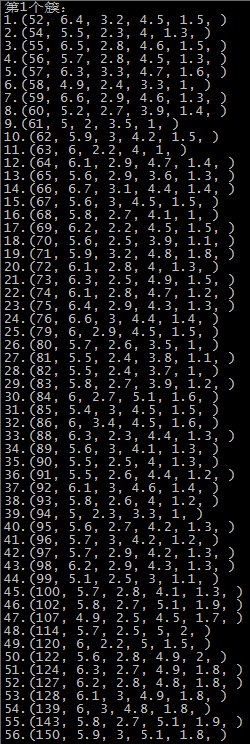
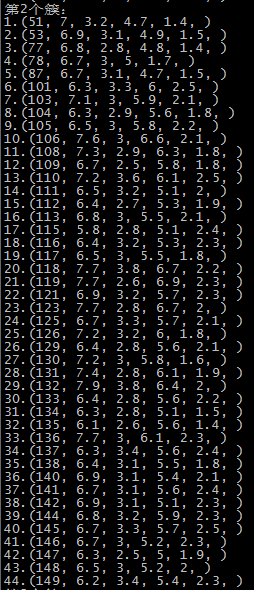
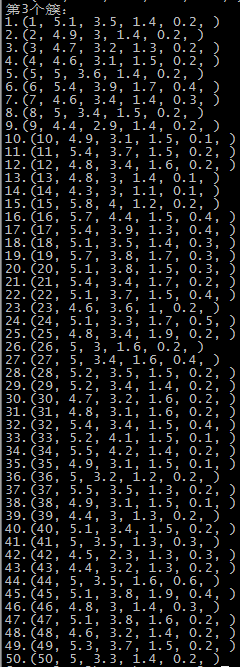
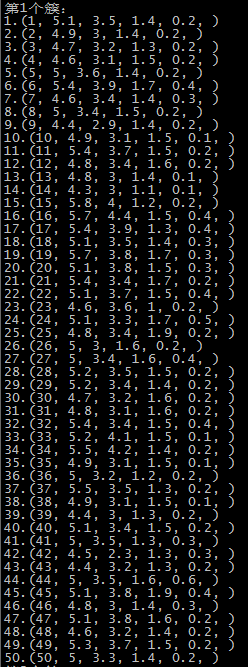
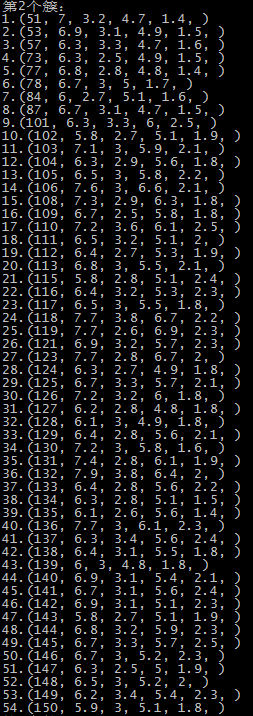
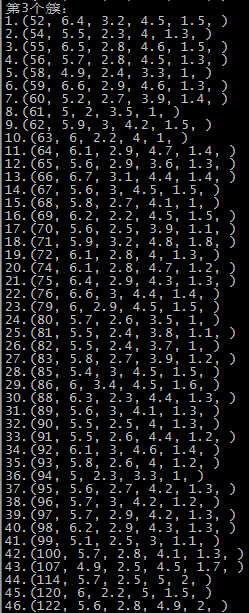
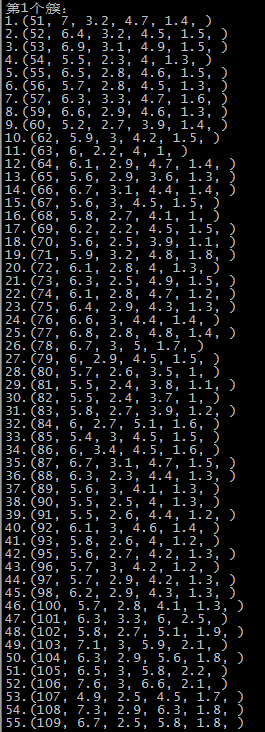
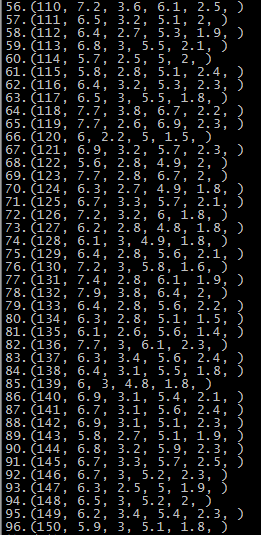
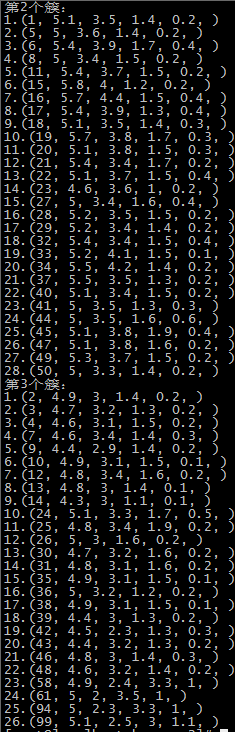
这里是随机选取的初始质心，以鸢尾花的数据集为例，原数据集中1-50为一个簇，51-100为第二个簇，101到150为第三个簇：

第一次运行结果 SSE=97.5905

第二次运行结果 SSE=98.1404

。。。

第五次运行结果 SSE=123.397

         由于初始质心是随机选取的，前两次还算正常，运行到第五次时，第一个簇基本包括了后51-150个记录，第二个簇和第三个簇包含了第1-50个记录，可能的原因就是随机选择初始点时，有两个初始点都选在了1-50个记录中。

参考：

[1]Pang-Ning Tan等著，《数据挖掘导论》，2011

[2]Jiawei Han等著，《数据挖掘概念与技术》，2008

[3]聚类分析中类数估计方法的实验比较

[4]http://www.cnblogs.com/vivounicorn/archive/2011/09/23/2186483.html

[5]一种基于贝叶斯信息准则的k均值聚类方法

[6]http://www.zhihu.com/question/19640394?nr=1¬i_id=8736954