好早之前的Za (我会说我连着两次打完了没保存导致重打了两次吗 
定义
树链剖分就是把树拆成⼀系列链,然后用数据结构对链进⾏维护
通常的剖分⽅法是轻重链剖分,所谓轻重链就是对于节点 u 的所
有⼦结点 v,size[v] 最⼤的 v 与 u 的边是重边,其它边是轻边
其中 size[v] 是以 v 为根的⼦树的节点个数,全部由重边组成的
路径是重路径
根据论⽂上的证明,任意⼀点到根的路径上存在不超过 \(logn\) 条
轻边和 \(logn\) 条重路径
定义
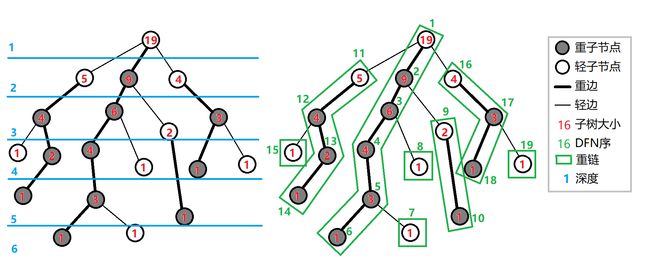
定义 重子节点 表示其子节点中子树最大的子结点。如果有相同的,任意取。如果没有子节点,就没有。
定义 轻子节点 表示剩余的子结点。
从这个结点到重子节点的边叫 重边 。
到其他轻子节点的边叫 轻边 。
若干条首尾衔接的重边构成 重链 。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链。
这个图超级清晰
构建
第⼀遍dfs
求出树每个结点的深度\(dep[x]\),其为根的⼦树⼤小\(size[x]\)
第⼆遍dfs
以根节点为起点,向下拓展构建重链
选择最⼤的⼀个⼦树的根继承当前重链
其余节点,都以该节点为起点向下重新拉⼀条重链
给每个结点分配⼀个位置编号,每条重链就相当于⼀段区间,用
数据结构维护
把所有的重链首尾相接,放到同⼀个数据结构上,然后维护这⼀
个整体即可
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
if((v=e[i].v)==fa) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mxs) son[u]=v,mxs=sz[v];
}
}
void dfs2(int u,int topf){
dfn[u]=++idx;
wt[idx]=a[u],top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u],v;i;i=e[i].nxt){
if((v=e[i].v)==f[u]||v==son[u]) continue;
dfs2(v,v);
}
}实战
luogu模板
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式:$ 1 x y z $ 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式:$ 2 x y $表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式:\(3\ x\ z\) 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式:$ 4 x $表示求以x为根节点的子树内所有节点值之和
#include
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
#define Abs(x) ((x)<0?-(x):(x))
#define ls (o<<1)
#define rs (o<<1|1)
const int N=1e5+10,M=1e5+50,inf=0x3f3f3f3f;
int n,m,rt,P,a[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
int head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
int idx=0,dfn[N],f[N],son[N],top[N],dep[N],sz[N],wt[N];
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
if((v=e[i].v)==fa) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mxs) son[u]=v,mxs=sz[v];
}
}
void dfs2(int u,int topf){
dfn[u]=++idx;
wt[idx]=a[u],top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u],v;i;i=e[i].nxt){
if((v=e[i].v)==f[u]||v==son[u]) continue;
dfs2(v,v);
}
}
struct node{int add,val;}t[N<<2];
void pup(int o){t[o].val=t[ls].val+t[rs].val;}
void updnode(int o,int l,int r,int k){
t[o].val=(t[o].val+(r-l+1)*k)%P,t[o].add=(t[o].add+k)%P;
}
void pudw(int o,int l,int r){
if(!t[o].add) return;
int mid=l+r>>1;
updnode(ls,l,mid,t[o].add),updnode(rs,mid+1,r,t[o].add);
t[o].add=0;
}
void upd(int o,int l,int r,int x,int y,int k){
if(l>y||r>1;
upd(ls,l,mid,x,y,k),upd(rs,mid+1,r,x,y,k);
pup(o);
}
void build(int o,int l,int r){
t[o].add=0;
if(l==r){t[o].val=wt[l];return;}
int mid=l+r>>1;
build(ls,l,mid),build(rs,mid+1,r);
pup(o);
}
int query(int o,int l,int r,int x,int y){
if(l>y||r>1,ans=0;
ans=(ans+query(ls,l,mid,x,y))%P,ans=(ans+query(rs,mid+1,r,x,y))%P;
pup(o);
return ans;
}
void updrange(int x,int y,int k){
while(top[x]!=top[y]){
if(dep[top[x]]dep[y]) swap(x,y);
upd(1,1,n,dfn[x],dfn[y],k);
}
int qrange(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]dep[y]) swap(x,y);
ans=(ans+query(1,1,n,dfn[x],dfn[y]))%P;
return ans;
}
void updson(int x,int k){
upd(1,1,n,dfn[x],dfn[x]+sz[x]-1,k);
}
int qson(int x){
return query(1,1,n,dfn[x],dfn[x]+sz[x]-1);
}
int main(){
// freopen("in.txt","r",stdin);
//freopen("and.out","w",stdout);
rd(n),rd(m),rd(rt),rd(P);
for(int i=1;i<=n;++i) rd(a[i]);
for(int i=1,u,v;i [HAOI2015]树上操作
P3178 [HAOI2015]树上操作 bzoj1036
有一棵点数为 N 的树,以点 1 为根,且树点有边权。然后有 M 个操作,分为三种:
- 操作 1 :把某个节点 x 的点权增加 a 。
- 操作 2 :把某个节点 x 为根的子树中所有点的点权都增加 a 。
- 操作 3 :询问某个节点 x 到根的路径中所有点的点权和。
==一个模板题
#include
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
#define ls (o<<1)
#define rs (o<<1|1)
const int N=1e5+10,M=1e5+50,inf=0x3f3f3f3f;
int n,m,rt,P;ll a[N],wt[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
int head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
int idx=0,dfn[N],f[N],son[N],top[N],dep[N],sz[N];
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
if((v=e[i].v)==fa) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mxs) son[u]=v,mxs=sz[v];
}
}
void dfs2(int u,int topf){
dfn[u]=++idx;
wt[idx]=a[u],top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u],v;i;i=e[i].nxt){
if((v=e[i].v)==f[u]||v==son[u]) continue;
dfs2(v,v);
}
}
struct node{ll add,val;}t[N<<2];
void pup(int o){t[o].val=t[ls].val+t[rs].val;}
void updnode(int o,int l,int r,ll k){
t[o].val+=(ll)(r-l+1)*k,t[o].add+=k;
}
void pudw(int o,int l,int r){
if(!t[o].add) return;
int mid=l+r>>1;
updnode(ls,l,mid,t[o].add),updnode(rs,mid+1,r,t[o].add);
t[o].add=0;
}
void upd(int o,int l,int r,int x,int y,ll k){
if(l>y||r>1;
upd(ls,l,mid,x,y,k),upd(rs,mid+1,r,x,y,k);
pup(o);
}
void upd2(int o,int l,int r,int x,ll k){
if(l==r){t[o].val+=k;return;}
pudw(o,l,r);
int mid=l+r>>1;
if(x<=mid) upd2(ls,l,mid,x,k);
else upd2(rs,mid+1,r,x,k);
pup(o);
}
void build(int o,int l,int r){
t[o].add=0;
if(l==r){t[o].val=wt[l];return;}
int mid=l+r>>1;
build(ls,l,mid),build(rs,mid+1,r);
pup(o);
}
ll query(int o,int l,int r,int x,int y){
if(l>y||r>1;ll ans=0;
ans+=query(ls,l,mid,x,y)+query(rs,mid+1,r,x,y);
pup(o);
return ans;
}
void updrange(int x,int y,ll k){
while(top[x]!=top[y]){
if(dep[top[x]]dep[y]) swap(x,y);
upd(1,1,n,dfn[x],dfn[y],k);
}
ll qrange(int x,int y){
ll ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]dep[y]) swap(x,y);
ans+=query(1,1,n,dfn[x],dfn[y]);
return ans;
}
void updson(int x,ll k){
upd(1,1,n,dfn[x],dfn[x]+sz[x]-1,k);
}
ll qson(int x){
return query(1,1,n,dfn[x],dfn[x]+sz[x]-1);
}
int main(){
// freopen("in.txt","r",stdin);
//freopen("and.out","w",stdout);
rd(n),rd(m),rt=1;
for(int i=1;i<=n;++i) rd(a[i]);
for(int i=1,u,v;i [ZJOI2008]树的统计
P2590 [ZJOI2008]树的统计 bzoj1036
一棵树上有n个节点,编号分别为1到n,每个节点都有一个权值w。
我们将以下面的形式来要求你对这棵树完成一些操作:
I. CHANGE u t : 把结点u的权值改为t
II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值
III. QSUM u v: 询问从点u到点v的路径上的节点的权值和
注意:从点u到点v的路径上的节点包括u和v本身
还是模板==
以后还是少用点宏定义 ==这个好恐怖
宏定义Max上去是将里面的数复制了一遍 如果放的是函数 那就会跑两次!! 然后t到飞起
#include
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
#define Abs(x) ((x)<0?-(x):(x))
#define ls (o<<1)
#define rs (o<<1|1)
const int N=30000+10,M=1e5+50,inf=0x3f3f3f3f;
int n,m,rt,P,a[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
int head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
int idx=0,dfn[N],sz[N],f[N],dep[N],son[N],top[N],wt[N];
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
if((v=e[i].v)==fa) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(mxs>1;
if(x<=mid) upd(ls,l,mid,x,k);
else upd(rs,mid+1,r,x,k);
pup(o);
}
void build(int o,int l,int r){
if(l==r){t[o].mx=t[o].sum=wt[l];return;}
int mid=l+r>>1;
build(ls,l,mid),build(rs,mid+1,r);
pup(o);
}
int qsum(int o,int l,int r,int x,int y){
if(l>y||r>1,ans=0;
ans=qsum(ls,l,mid,x,y)+qsum(rs,mid+1,r,x,y);
return ans;
}
int qmax(int o,int l,int r,int x,int y){
if(l>y||r>1,ans;
ans=max(qmax(ls,l,mid,x,y),qmax(rs,mid+1,r,x,y));
return ans;
}
int Qsum(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]dep[y]) swap(x,y);
ans+=qsum(1,1,n,dfn[x],dfn[y]);
return ans;
}
int Qmax(int x,int y){
int ans=-inf;
while(top[x]!=top[y]){
if(dep[top[x]]dep[y]) swap(x,y);
ans=max(ans,qmax(1,1,n,dfn[x],dfn[y]));
return ans;
}
int main(){
// freopen("in.txt","r",stdin);
//freopen("and.out","w",stdout);
rd(n),rt=1;
for(int i=1,u,v;i [NOI2015]软件包管理器]
P2146 [NOI2015]软件包管理器 bzoj4196
开始把题理解错了...
安装 查询从安装点到根节点有多少个未安装
卸载 查询以卸载点为根节点的子树有多少个安装了的
==还是一个模板
#include
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
#define Abs(x) ((x)<0?-(x):(x))
#define ls (o<<1)
#define rs (o<<1|1)
const int N=1e5+10,M=1e5+50,inf=0x3f3f3f3f;
int n,m,rt,P,a[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
int idx=0,dfn[N],sz[N],dep[N],son[N],f[N],top[N];
int head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
dfs1((v=e[i].v),u);sz[u]+=sz[v];
if(mxs>1;
if(t[o].tg==1) upd1(ls,l,mid),upd1(rs,mid+1,r);
else if(t[o].tg==2) upd2(ls,l,mid),upd2(rs,mid+1,r);
t[o].tg=0;
}
void install(int o,int l,int r,int x,int y){
if(l>y||r>1;
install(ls,l,mid,x,y),install(rs,mid+1,r,x,y);
pup(o);
}
void uninstall(int o,int l,int r,int x,int y){
if(l>y||r>1;
uninstall(ls,l,mid,x,y),uninstall(rs,mid+1,r,x,y);
pup(o);
}
void work(int x,int typ){
if(typ==1){
while(top[x]!=rt){
install(1,1,n,dfn[top[x]],dfn[x]);
x=f[top[x]];
}
install(1,1,n,dfn[rt],dfn[x]);
}
else{
uninstall(1,1,n,dfn[x],dfn[x]+sz[x]-1);
}
printf("%d\n",ans);
}
int main(){
// freopen("in.txt","r",stdin);
//freopen("and.out","w",stdout);
rd(n),rt=0;
for(int i=1,fa;i [SDOI2011] 染色
P2486 [SDOI2011]染色 bzoj2243
#include
#include
#include
#include
#include
#include
const int N=110000,MAX=110000;
#define ls (o<<1)
#define rs (o<<1|1)
using namespace std;
int n,m,a[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
struct node{int sum;int lc,rc,tg;}t[MAX<<2];
int head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
int idx=0,dfn[N],f[N],son[N],top[N],dep[N],sz[N],wt[N];
void dfs1(int u,int fa){
dep[u]=dep[fa]+1,f[u]=fa,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
if((v=e[i].v)==fa) continue;
dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>mxs) son[u]=v,mxs=sz[v];
}
}
void dfs2(int u,int topf){
dfn[u]=++idx,wt[idx]=a[u],top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=f[u]&&v!=son[u]) dfs2(v,v);
}
void pup(int o){
t[o].sum=t[ls].sum+t[rs].sum;
if(t[ls].rc==t[rs].lc)t[o].sum--;
t[o].lc=t[ls].lc,t[o].rc=t[rs].rc;
}
void updnode(int o,int k){
t[o].lc=t[o].rc=t[o].tg=k;
t[o].sum=1;
}
void pudw(int o){
if(t[o].tg) updnode(ls,t[o].tg),updnode(rs,t[o].tg),t[o].tg=0;
}
void build(int o,int l,int r){
if(l==r){t[o].lc=t[o].rc=wt[l],t[o].sum=1;return;}
int mid=(l+r)>>1;
build(ls,l,mid),build(rs,mid+1,r);
pup(o);
}
node query(int o,int l,int r,int x,int y){
if(x<=l&&r<=y) return t[o];
pudw(o);
int mid=l+r>>1;
if(y<=mid) return query(ls,l,mid,x,y);
else if(x>mid) return query(rs,mid+1,r,x,y);
else{
node ans,L,R;
L=query(ls,l,mid,x,y),R=query(rs,mid+1,r,x,y);
ans.lc=L.lc,ans.rc=R.rc,ans.sum=L.sum+R.sum;
if(L.rc==R.lc) --ans.sum;
return ans;
}
pup(o);
}
void upd(int o,int l,int r,int x,int y,int k){
if(l==x&&r==y){updnode(o,k);return;}
int mid=(l+r)>>1;
pudw(o);
if(y<=mid)upd(ls,l,mid,x,y,k);
else if(x>mid)upd(rs,mid+1,r,x,y,k);
else{
upd(ls,l,mid,x,mid,k);
upd(rs,mid+1,r,mid+1,y,k);
}
pup(o);
}
void qrange(int x,int y){
int pre1=-1,pre2=-1,ans=0;node nw;
while(top[x]!=top[y]){
if(dep[top[x]]dep[y])swap(x,y);
upd(1,1,n,dfn[x],dfn[y],k);
}
int main(){
freopen("in.txt","r",stdin);
rd(n),rd(m);
for(int i=1;i<=n;++i) rd(a[i]);
for(int i=1,u,v;i