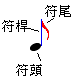
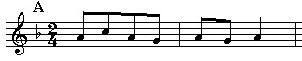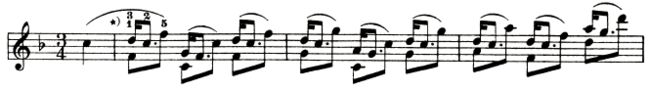对于音乐,我一直有一个在家人朋友面前装逼的梦想,不过唱歌跑调,学了学吉他,技术也是比较水。尤其对谱子记忆特别困难,对于音没有特别的感受,乐理基本上是白痴,一直以来对它都是无比敬畏,我认为乐理是一本非常高深的理论。
乐理的基本内容包括:和声、调式、节奏、结构、曲式。我先从简单的原理开始吧。
一、音
声音是物体振动通过介质传给大脑感受到的。所以就跟色彩、气味一样,即使相同的音对于不同的人来说,都可能由于个体差异产生不同的感受。
声波的性质
声波是一种机械波,由物体(声源)振动产生,声波传播的空间就称为声场。声波在气体和液体介质中传播时是一种纵波,但在固体介质中传播时可能混有横波。它的基本参数是频率 f (frequency)和振幅(amplitude)。频率是某一质点以中间轴为中心,1秒内来回振动的次数(单位为赫兹Hz),而质点完成一次全振动经过的时间为一个周期 T,其单位为秒。显然,f=1/T。
纯音:以某个固定频率进行简谐振动所产生的声波。
复合音:由多个纯音组合而成。产生方式多种多样,有两种在音乐中最为常见:一种称为谐波叠加,一种称为拍音叠加。
谐波
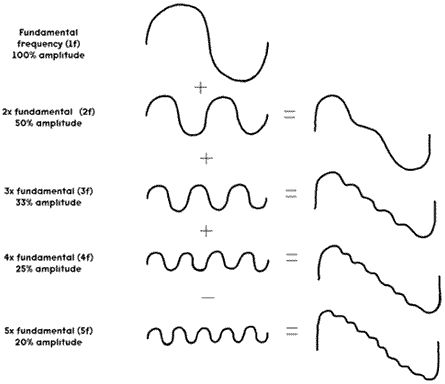
我们将一个标准的正弦波作为基准,称作基波。谐波就是比基波的频率高整数倍的波,音乐人往往将谐波称为“泛音”。例如某个纯音声波的频率是f,将此纯音作为基波,其谐波的频率可为2f、3f、4f、……,这些谐波分别称为二次谐波、三次谐波、四次谐波等。
若一个复合音由基波与及其谐波相叠加构成,则称该复合音为谐波叠加,它的频率为基波频率。基波与谐波叠加构成复合音的过程见下图所示。
实际上,所有传统乐器所发出的音都是复合音,由振幅最大的基波和一些列振幅较小的谐波叠加构成。那么我们就可以给出单音的定义了:单音特指单一乐器演奏独立的一个音发出的声波(谐波叠加),其基波的频率称为音高。不同乐器的单音所叠加的谐波在频率和振幅上都不相同,因此乐器的音色千差万别。
拍音
拍音是另一种复合音,它是由来自同一种乐器或不同乐器的两个单音相互叠加,形成具有规律性强弱变化的振动。与谐波不同的是,拍音一般要求这两个音的振幅相近,但不要求频率为倍数关系。这样的声音会让人难以忍受。在钢琴调律过程中,钢琴“假拍”现象也是较常碰到的情况。也就是说单根琴弦也能产生一定频率的拍音。
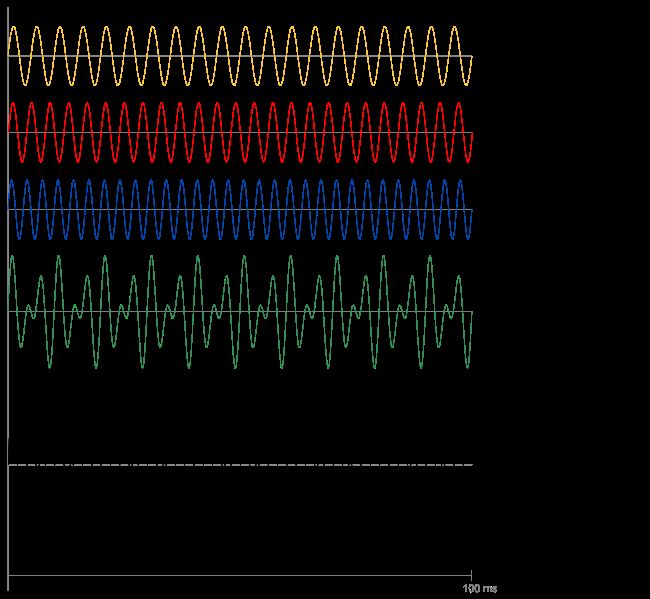
单音本身由纯音叠加而来,单音相互叠加,情况将会变得非常复杂。所以以纯音的叠加来解释拍音的形成。上图中黄色、红色和蓝色的波型分别为频率200Hz,250Hz和300Hz的纯音。黄色与蓝色两纯音叠加形成绿色的拍音波形,黄红蓝三纯音叠加形成黑色的拍音波型。
分析可知,每当两个单音的波峰相遇就形成拍音的波峰,波谷相遇就形成拍音的波谷,这样的复合音从波型看起来存在周期性的振幅变化,像节拍一般,因此称为拍音。拍音的频率与叠加的两个单音的周期(频率的倒数)的比值相关,如果两个单音的频率都是整数,那么拍音的频率就等于它们周期最小公倍数的倒数。
频率相差一倍的两个单音叠加形成的拍音,其频率等于较低的音的频率,这样的拍音听起来就像一个音。例如钢琴上的任意两个Do音之间的频率都相差一倍,点击这里有一架在线钢琴,t键是中央Do,s键是高音Do,同时按下就形成了上述拍音。
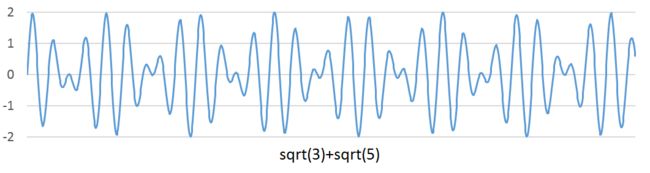
如果两个单音中至少有一个是无理数,那么拍音的情况就要复杂一些了。此时两个单音的波峰永远不会相遇,波谷亦然,只会出现非常接近的情况。如果两个波的波峰以一个近似的周期s相互靠得很近,那么不太精确的人耳就会“认为”这两个单音的叠加形成了频率为1/s的拍音。这里面的原理确实比较复杂,我们举例子来说明。比如单音a的频率fa=√3,单音b的频率为fb=√5,它们的周期分别为sa=1/fas和sb=1/fb,它们的波形如图所示。
无论是看起来还是理论分析,这两个波的波峰永远不可能相遇。下面我们把这两个波进行叠加,便得到图所示波形。
两波叠加后形成了周期近似为4×sa≈3×sb4×sa≈3×sb的拍音。这是因为√3/√5≈0.7746,接近于0.75,也就是3:4。因此这个拍音的“听感频率”大约为√5/4到√3/3之间。
为了深入解释什么是拍音,需要先了解一些名词:乐音:发音物体有规律地振动而产生的具有固定音高的音。音级:在通行的十二平均律中,互为倍频关系的两个音(含)之间,一共有(12345671)八个自然音级。度:就是音与音之间距离的衡量单位。例如,八度音。音程:音与音之间音高的距离,就叫做音程。根音:音程中低音(root)。根音上的三度音称为三音,根音上的五度音称为五音。任何音阶中的任意音级均可作为根音,于其上方加入三音与五音而构成三和弦,每个和弦视其根音在音阶上的名称或音级数而命名。在和弦的基本形态中是最下端的一音。中音:已一个三度音程组成的三和弦 根音 三音(中音)五音(冠音)。低的叫根音。冠音: 音程中的两个音,低音叫做“根音”(也叫下方音)、高音叫做“冠音”(也叫做上方音)。
吻合谐音:某一乐音的某次谐音与另一乐音的某次谐音的频率相等。
拍:如果构成某种音程的根、冠两音的吻合谐音的频率出现偏离,则两个声波相互干涉而产生 拍。其合成波出现周期性的幅值变化。单位时间内的拍的数量称作 拍频 。拍频适中的、能为人耳所感受到的拍就称作 拍音 。当拍的拍频过快而我们很难或无法分辨时,是不会对调律提供任何帮助的。
纯点:吻合的谐音的频率 。高于纯点的频率偏离所产生的拍是 正拍, 低于纯点的频率偏离所产生的拍是 负拍。音程谐音持续吻合的状态,我们称之为“ 纯 ”。喵音是一种非常接近纯的拍音。
“纯”和“准”:十二平均律所对应各音的音高频率称作 准点 。当某音音高达到准点时,我们称之为“ 准 ”。拍音是我们进行调律的判断依据,而拍音要对照纯点而言,因此我们把音程的纯点作为调律的参照点——在调律时,我们把音程的纯点作为参照点, 按照“准”的要求,听辨拍音状况,放宽或收窄音程,使音高达到“准点”。
十二平均律半音间的频率比为 12 √2,除同度、八度音程外,各种音程的频率比不呈简单的整数比。也就是说,在十二平均律制中,除同度、八度音程(“纯”即是“准”)外,其它各音程间均有拍存在。我们正是根据各音程之间的拍音数量来判定某一个音是否“准”了。在分律和检验时均是如此。换句话说,有的音程(同度、八度音程)没拍就“准”了,有的音程有一定的拍就“准”了。
假拍:有些琴弦自身就带有的拍音,我们称之为假拍。如果我们调试的音程中有某一根(或两根)琴弦带有假拍,最“纯”点有拍音,且拍音等于两根弦各自的假拍相叠加。有假拍的情况下,八度、同度在最“准”的位置仍有相对最少的拍存在。
拍音听辨:“听音头”“听音尾”。
音的四种性质
高低:振动频率。人耳所感受的范围约为:16~20000Hz,音乐中所采用的是16~4000Hz。比较悦耳的范围60~1000Hz,国际通用标准音a1频率为440Hz,叫做A4,中央C为262Hz,也称小字一组C,C4。
音乐中的乐音都是有固定音高的,每个音波之间的波长是相等的。噪音没有固定音高,音波是不规则的,波长也不相等,但是噪声也有相当的表现力。
长短(音值):音的长短是由发音物体振动的时间延续的长短句定的。
强弱(音量):音的强弱是由发音体振动的幅度大小决定的。
音色:音色就是不同乐器的单音所叠加的谐波在频率和振幅上都不相同产生的。
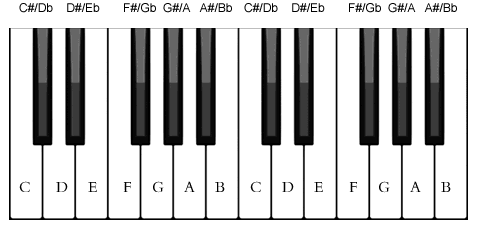
二、十二平均律
目前世界上最通用的音律体系——十二平均律的历史非常悠久,最早可以追溯到公元400年左右的中国人何承天。公元16世纪的明朝人的朱载堉(朱元璋的九世孙)将十二平均律发展为完整的理论水平,到16世纪末,由当时教皇国的传教士利玛窦将十二平均律法从中国带回西方,直到17世纪才开始在欧洲大陆广泛流传。中国人发明了十二平均律,但中国文明自清朝开始的衰落,使得中国古典音乐的理论水平与西方音乐的差距越来越大,直到没落于下里巴人。
当西方有了十二平均律这一黄金律法,新的和声理论、自然调式(念“Diao Shi”,不念Debug)和各种相关调性也就随之产生了,而这些系统则几乎全是由西方发展出来的。我们目前听到的所有古典音乐和现代音乐(包括流行、摇滚、歌舞剧)都是基于西方的音乐理论。
十二平均律
十二平均律是音乐中最底层的系统,规定了两个单音的相对音高。十二平均律体系将一个“纯八度”分成12份,每份称为1个半音,两份为1个全音,以此定出所有中间的单音。
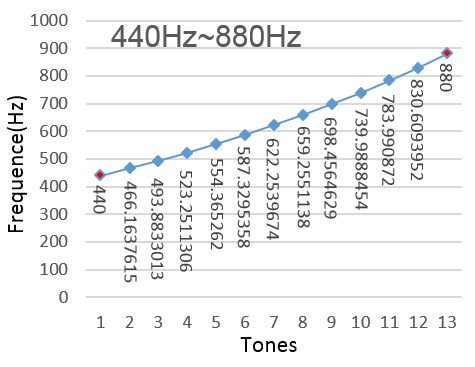
如果将f设定为440Hz,从f到2f这13个单音的频率就可以用前述公式算出。
十二平均律系统规定任两个相邻的音之间的音数为0.5,也就是一个半音。
将音数为1的音程称为全音,将音数为0.5的音程称为半音。每一个音程还有其它的名称,这叫做“异名同音”。例如小三度又称为增二度,大六度又称为减七度等等。
三全音:音程增四度减五度,这两个音程都包含三个全音。(F到B,增四度,B到F,减五度)
音程的转位:转位前的度数和转位后的度数相加等于9。转位后的技巧:大小增减是互换,纯音程不变。
乐理发展史——相对音高的确定
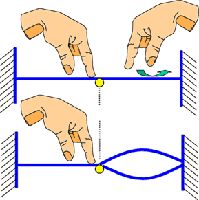
人们很早就发现长度比为1:2的两根弦同时拨响可以发出非常协调的声音,但仅仅使用2倍关系的弦长所构造出来的音过于单调了,可以说根本不足以形成音乐,因此人们就尝试用其它的弦长比来发声。一根固定在平面上的弦如果从中间任意位置按在平面上,就形成了左右两段成不同长度比且可以分开振动的弦,人们就是用这种方法尝试不同的弦长比的。
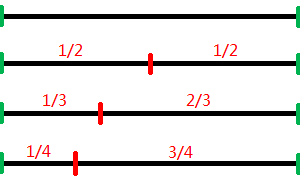
我们把原弦长所发出的频率记为f。用手指按在弦的正中间,即1/2处,形成的两段弦长是相等的,它们发出的声音频率都为2f,这样纯八度音程就形成了。
接下来人们尝试在纯八度音程的中间找到其它的音,首先按在弦长的1/3处,在较长的那一段人们听到了一个新的音,它的频率是3f/2,听起来与f非常协调。信心满满的人们接下来又尝试按在弦长的1/4处,但较长那一段的音听起来虽没有前一个音程那么协调,但也挺不错,它的频率是4f/3。用同样的方法人们又得到5f/4、6f/5、7f/6……然而,人们很快就遇到了麻烦:首先,新得到的音的频率与f的叠加变得越来越不协调(其原因将在下文“和声”部分详细说明);其次,新产生的音与前一个产生的音之间也不存在任何协调关系,这样下去是不可能产生悦耳动听的音乐的。人们只能另辟蹊径。
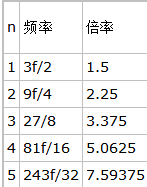
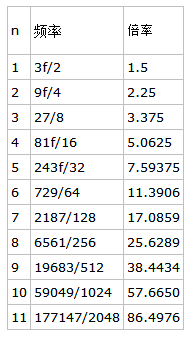
不过这时人们已经获得了3种最简单也最重要的弦长比,分别是1:2、2:3和3:4,它们来自于3个不同的分割点。为了获得新的频率,又要与f或之前已产生的频率保持协调,那么能否以这3种分割点为基础,从较长的那一段再以同样的比例继续细分呢?当然是可行的,因为协调性可以传递!1/2即是原弦长的一半,再将其细分为1/2就得到原弦长的1/4,协调性没问题,但这仍然是纯八度音程,没有出现新的音程。而从2/3处再细分情况就大不相同了,2/3再细分2/3,就得到了与原弦长比为4:9的长度。9f/4是一个全新的频率,显然它与3f/2的协调程度和3f/2与f的协调程度是相同的。再从4/9中分割出2/3,得到频率27f/8……一直用(2/3)n(2/3)n切分下去就得到了如下的频率序列:
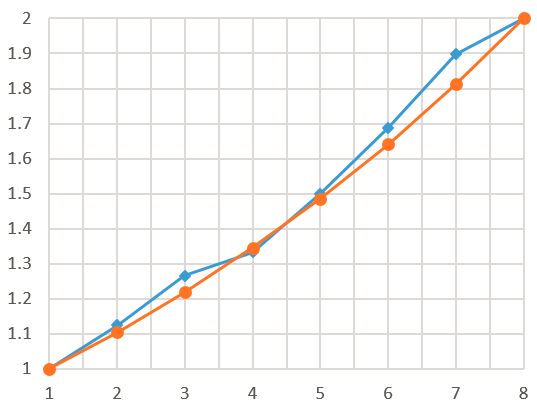
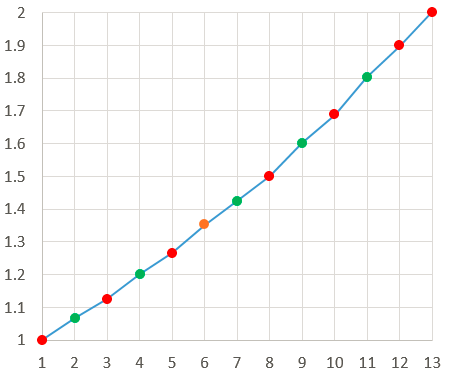
我们把这5个音和4f/3合起来看,这6个音(黑x表示)分别隶属于3个不同的纯八度音程。将这6个音的频率都除以所在纯八度的最低频率,我们就确定了一个纯八度音程中的相对位置。
挺奇妙的不是吗?与理想的指数曲线相比误差并不大。这不仅意味着音和音之间存在协调关系,而且按这样的倍率关系,从任意置开始的连续7个音都能形成一条听起来相当不错的音阶。这就是7音阶的来历。
这种方法由f产生的第1个音是3f/2,除4f/3之外的其它因都是由3f/2产生,而f到3f/2是纯五度关系,因此这个方法被人们称为“五度相生律”。7个音分别是:{1, 1.125, 1.265625, 1.333, 1.5, 1.6875, 1.8984375},它们对应的音名是:{C, D, E, F, G, A, B}。
随着音乐水平的不断发展,这7个音慢慢变得不够用了,而且相邻两个音之间的频率比并不统一,跟不上乐器音准的提高速度。因此后来人们又发明出了十二平均律系统。我们现在知道,当相邻的音都为等比关系时,音阶才最平滑。而原始7音阶中的第3个音和第7个音看起来是那么突兀,这样构造出来的音乐确实不够好听。后来有人提出“纯律”学说,有人认为纯律和五度相生律都是毕达哥拉斯提出或整理的,也有人认为纯律在中国2400年前的战国时代就已开始应用,还有人说是古希腊学者亚理斯托森努斯发明……不过可以肯定的是纯律在2000多年前就已被人类所掌握。纯律构造音阶的方法与五度相生律不同,它是由纯五度(2:3)和大三度(4:5)为素材确定7音阶的律制。纯率生成的7个音的频率分别是:{f, 9f/8, 5f/4, 4f/3, 3f/2, 5f/3, 15f/8}。
好是好点,不过就那么一点点而已,而且还打破了五度相生律产生的内部协调性。此外7个音也开始显得不够用了,人们希望通过变调使得音乐更加丰富,看来还得继续探索。之前人们为了计算第7个音,就要计算2/3的5次幂,这对于2000多年前的计算水平来说确实有点难了。然而数学的发展又一次给音乐带来了新生。人们通过计算发现,2/3的12次幂约为129.74634,约等于基准频率f上面的第7个八度音的频率,那么可否继续应用五度相生律再产生一些音呢?
由这些倍率产生的12音阶为(用倍率除以它下面的第一个2^n而得):{1, 1.0679, 1.125, 1.2014, 1.2656, 1.3515, 1.4238, 1.5, 1.6018, 1.6875, 1.802, 1.8984}
震惊了吗?多么平滑的一条折线,而且新产生的音都被“均匀”地安插在了原先的7音阶中间。我们不得不惊叹造物主的神奇,这也是音乐是世界上唯一通行的语言的原因吧!由于之前的七个音和它们的音名{C, D, E, F, G, A, B}已经非常流行了,且新产生的音都可以看作是用原7音阶中的某个音升半音而得,因此这5个新产生的音就被叫做{C#, D#, F#, G#, A#},这也正是为什么E和F、B和C之间是半音的原因。
看起来已经很完美了,还有改进的空间吗?答案是有的。尽管五度相生律生成的12音阶已经相当平滑了,但仍然不是理想的“等比”音阶,这样就会导致一个潜在的问题。我们举例来说,大家都在KTV唱过歌,应该知道有些KTV的点播机有升降音的功能,当伴奏比较高而人声又吼不上去时,可以用降音功能把伴奏的音高统一降低一些,这样听起来仍然是非常自然的。比如一首歌原先的音的序列是,降低半音就是:。听起来仍然非常自然的原因在于这一序列内部的音程比例关系没有变,仍然是以2^(1/12)为基准的。在音乐术语中,这个过程叫做转调。然而要在五度相生律生成的12音阶系统中进行转调就会产生偏差,因为它内部的音程比例关系不是固定的。设想一群乐师给皇帝演奏曲目,乐器的音准都是预先调好的,结果皇帝一时兴起想高歌两句但又唱不上去高音,就命令乐师低两个音演奏,结果听到的伴奏完全不是刚刚那么回事了,这是多么尴尬的一件事。
后来人们又想出了各种修正的办法,比如构造一些等差数列来修正每个音与理想曲线的误差等等,但这些方法既复杂又不能从根本上解决问题。这时整个音乐界都在急迫的等待新律制的诞生。直到公元17世纪的明朝人朱载堉提出十二平均律,并由利玛窦带到西方,才拯救西方音乐界于水火之中。虽然十二平均律看起来那么完美,但也不是完全没有问题。有人认为十二平均律破坏了纯四度和纯五度的协调关系,也就是说我们之前讲的F音应该是C音频率的4/3=1.33333倍,G音应该是F音的3/2=1.5倍,而在十二平均律中它们的倍率分别是2^(5/12)≈1.33484和2^(7/12)≈1.49831。其实所差无几,不是吗?在通常的演奏音域范围内,人耳几乎是不可能听出这些区别的,这也是十二平均律沿用至今而五度相生律和纯律都已遭淘汰的原因。
绝对音高的确定
在人类音乐史上曾经出现过很多种不同的记谱法,大致可分为三大类:文字谱、符号谱和线谱。有不少学者认为文字谱和符号谱应该归为一类,但在下愚见认为,这二者处于不同的发展阶段,且由于文字系统的复杂性(表音文字和表意文字等),文字谱的意义与符号谱是完全不同的。
尽管世界上任何一个地方的人类都在数千年前就开始创造音乐了,但是由于东西方文明的巨大差异,导致发展出了完全不同的记谱系统。早在公元前25世纪,古埃及人就已经制造出了至少几十种各不相同的乐器。尽管现在已经无法考证古埃及人是如何记录音符的,但几乎可以肯定的是:他们已经发展出了比较完善的音乐理论,并且使得每一种乐器都能够合理的校准来配合大型乐队的演奏。
在东方,最古老的乐谱出自于华夏文明,春秋时期的《礼记·投壶》记载了至今发现的最古老乐谱:鼓谱,它是用符号方框和圆圈记录的。到汉代司马迁的《史记》“律书第三”中写到:“……九九八十一以为宫。三分去一,五十四以为徵(念zhi,三声)。三分益一,七十二以为商。三分去一,四十八以为羽。三分益一,六十四以为角。”。它的意思是取一根用来定音的竹管,长为81单位,定为“宫音”。然后将81乘上2/3,就得到54单位,定为“徵音”。将徵音的竹管长度54乘上4/3,得到72单位,定为“商音”。将商音72乘2/3,得48单位,为“羽音”。羽音48乘4/3,得64单位,为“角音”。而这宫、商、角、徵、羽五个音高,被称为中国的五音。这种音律方法称为“三分损益法”。(宫商角徵羽,非别为12356)
后来人们继续应用三分损益法构造出了另外7个音,并给这一共12个音都起了名字。与现代音名的对照分别是:黄钟(C),林钟(G),太簇(D),南吕(A),姑洗(E),应钟(B),蕤宾(Gb/F#),大吕(Db/C#),夷则(Ab/G#),夹钟(Eb/D#),无射(Bb/A#),仲吕(F)。以这些音名第一个字作为简写就是中国古代使用最广泛的记谱法:“乐律谱”,它属于文字谱的一种。
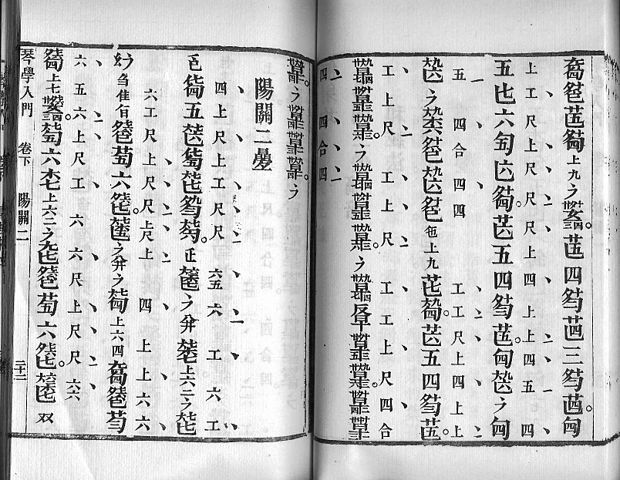
但是乐律谱的记载太麻烦了,因此人们又发明了“工尺谱”。唐朝已经有工尺谱,传到宋朝极为流行。它具有7个唱名:上、尺、工、凡、六、五、乙,大至对应于西方的{Do, Re, Mi, Fa, So, La, Si}。相信最初工尺谱是某种乐器的乐谱,是固定音名,但后来在不同乐器和乐种广泛流传以后,工尺谱逐渐变成不固定的唱名。
工尺谱是一种符号谱,但它并非一种精确的记谱法,有很大的空间让表演者作即兴发挥。在传统中国音乐里,乐谱只是一个记载的媒体,表演者并不会完全依据乐谱演奏,他可以加花(加上装饰音),在节奏上也有一定的自由。至于如何演奏才是合适的手法,是约定俗成的,以师父传徒弟的口授心传的方式继承。因此不同流派会有不同的演绎风格,这也是导致中国古代乐理水平进步相当缓慢的主要原因。
西方最早的乐谱出现在古希腊,当时是刻在石碑上的符号谱,难记难读,流传很少。后来人们觉得用符号表示音符实在太过麻烦,就尝试在音符间加了一条线,用这条线来代表一个标准音高。后来人们又开始增加线的数量,到11世纪,意大利乐理大师桂多通过对纽姆谱的改进,发明了四线谱,并发从一首圣歌的歌词中提取出了六个音的唱名ut、re、mi、fa、so、la。这就是五线谱和七唱名的前身。
在16世纪之前,西方一直没有一种统一的记谱法,符号的、一线的、两线的、三线的、四线的都有。直到公元十六世纪,五线谱诞生之后才逐渐一统江湖,形成全欧洲音乐人的标准记谱法。而五线谱的真正普及则是发生在17世纪,巴洛克时期的事情了。
这时的五线谱就已经和现代五线谱基本相同了。有了统一的记谱法,各地的音乐家们开始更为广泛的沟通和交流,而这时人们慢慢地意识到制定标准音高的重要性。要知道一个17世纪的英国教堂管风琴,使用的音高可能就比同城市中平民使用的键盘乐器低了五个半音。这样的情况对于音乐交流来说简直就是灾难。在1720年的英国音笛演奏中央A的频率为380Hz,而巴赫在汉堡市、莱比锡及魏玛等地使用的管风琴则以480Hz表示同一个音符,这两者约差四个半音。换句话说,1720年的英国音笛演奏的A音在巴赫那边会被认为是F音。
自18世纪早期,音叉(于1711年发明)的使用确实为音高带来了一个可靠的标准,然而差异仍然无法避免。比方说,亨德尔在1740年使用对应为A音的音叉,其频率为422.5赫兹,但在1780年时他使用同样对应A的音叉则有不同的频率:409赫兹,后者低了将近一个半音。不过,到了十八世纪末,中央C上的A所使用的频率渐渐地演进成在400赫兹到450赫兹之间。
上面提到的频率乃是经过现代仪器测量所得,当时的音乐家并没有方法得到如此准确的数值。虽然马兰·梅森在16世纪早期便对声音的频率有了初步的了解,直到十九世纪,在德国物理学家约翰.施布雷在1830年所做的努力之前,人们都没有足够精确的科学方法测量频率。至于用赫兹取代每秒循环次数,则是直到20世纪才做出的改变。
法国政府曾在1859年2月16日通过了一个法案定义中央C上的A为435赫兹。这是把音高尺度标准化的第一个尝试。这个标准之后在法国之外也非常流行,随着时间发展它渐渐从法国音高、大陆音高,最后甚至被称为国际音高。这个标准音域使得中央C的频率调整为约258.65赫兹。而另有一个称为“哲学的”或“科学的”的音高标准,把中央C定义为256赫兹,为此必须把A音调为约430.54赫兹。由于此法提供了一些数学上的便利,所有的C音都是二的次方(C1=32、C2=64、C3=128、C4=256),因此也得到了一些的支持者。不过比起A = 435赫兹,此法并没有得到官方的认可,也因此没有被大量采纳、使用。此种频率规格即称为“物理学音高”。
1926年,美国乐器厂商首先制定了以440Hz作为A音的标准,并以此标准生产乐器。要知道那时的美国音乐实力已经强大到足以与欧洲抗衡,而美国的乐器则更是行销全球。因此到1936年美国标准委员会正式推荐将中央C上面的A音的频率定为440Hz。1955年,国际标准委员会ISO正式接受这一推荐,A-440就成为了ISO的第16号标准。从那时起,全世界的音乐就都在一个调上了。
三、五线谱
五线谱是一种音乐语言,可以用来记录几乎任何形式的音乐。五线谱中记录的最主要的东西就是音符,一个音符表达一个单音,每一个音符都具有绝对的音高。也就是说五线谱上的同一个音符在不同乐器上演奏出来的音高是相同的(忽略调校的差异)。
五根线从低到高分别称作第一线、第二线、第三线、第四线和第五线。五根线中间的四个区间分别称为第一间、第二间、第三间和第四间。这些“线”和“间”都对应不同的音高。图最左边的符号是高音谱号,现在常用的谱号只有四种:高音谱号、中音谱号、次中音谱号和低音谱号,这里先介绍最常用的高音谱号。高音谱号代表该五线谱是一个高音谱,即确定了标记在线和间上的音符的音高。高音谱号中间的那个圈的圆心表示一个称作G的音的位置,而高音谱号本身也是由大写字母G演化而来的。历史上还出现过位置更靠下的高音谱号,不过现在已经不再使用了。
高音谱表的三线为小字一组的b;中音谱表的三线为中央c,即小字一组的c;低音谱表的三线为小字组的d。可以大概认识一下五线谱中的符号:
b:降号,画在第三线上表示该谱的调性是F大调。
节拍:例如:以四分音符为1拍,每小节2拍。
竖线:小节标记,两条竖线之间是一个小节。
唱名是由一位意大利音乐理论家桂多·达莱佐从一首拉丁语圣歌的歌词中抽取出来的。而音名则是由后来的英国人嫌拉丁唱名太麻烦,就用英语字母代替了。但无论是过去还是今天,A都是基准音(与主音概念不同,注意区别),ABCDEFG这样7个音连在一起形成的音阶称为“小调音阶”,不过后来大调比小调更为普及,便趋向于使用“大调音阶”(CDEFGAB)的主音C作为一个纯八度音程的开始。
如果音符过高或过低,在五条线中画不下了,还可以在五根线的上面或着下面加线,这些线叫做“下加X线”和“上加X线”,X可以是“一”、“二”、“三”……。
人们规定高音谱中第二间的La,频率是440Hz。以A为基准,其它音符的频率就可以用十二平均律系统从中音A推算出来了,这就是基准音A的概念。
五线谱中的相对音程
第一线上的音名是E,第一间的音名是F,其它以此类推。右侧的“全”和“半”表示相邻两个音符之间的音程是全音还是半音。高音五线谱中,我们知道第二间的A的音高定为440Hz,再确定了音符之间的相对音程,我们就可以开始推算所有其它单音的频率了。
科学记音法:即两个字符表示一个音:XN。其中X为音名,可以是{C, D, E, F, G, A, B}中的任意一个;N为该音的序号,从0开始由低到高编号。
比A4低纯八度的音符是A3,其频率为A4频率的一半,即220Hz,比A4高纯八度的音符是A5,频率为A4频率的二倍,即880。A0到A7间所有A音的频率见下表:
例如,由于第三间的C音(即C5)与其下方第一个A音,即A4之间的音程是小三度,音数t=1.5,因此C5的频率为:440×2^(1.5/6)≈523.25113Hz。也可通过纯八度音程的倍率关系计算,比如C4的频率为C5的1/2,约为261.62557Hz。
升降记号
五线谱中,音符的后面可以添加升降标记,表示该音符升高半音或降低半音。升号为#(sharp),降号为b(flat)。升降号要写在音名之后:A#。
有的降音都可以由另一些音的升音代替,比如Bb就是A#,Gb就是F#。那既然如此,为什么不用升号代替全部的降号呢?原因就是为了可读性。
如果一段谱子中的某个音符几乎都要升半音或降半音处理,那就可以在高音谱号的右侧,这个音符所在的一条线或一个间上标记升降号。
所示乐谱中,第三线上标记了一个降号b,表示这个谱子里的所有B音都需降半音,除非另外在个别音符上标记升降或还原记号。音符被升降半音后的频率可根据之前学过的相邻音符之间的频率倍数关系计算。升高半音后的频率为原频率的2^(1/12)倍,降低半音后的频率为原频率的1/2^(1/12)倍。比如C5升高半音的频率即为554.3653Hz。
双音谱
标有高音谱号的上面一排是高音谱,标有低音谱号的下面一排是低音谱,它们分别对应钢琴健盘上不同的键区。
其实低音谱中的音名也没有那么难记,实际上它和高音谱是相互连接的,中间刚好只隔了一条加线。高音谱的下加一线就是低音谱的上加一线,而这条线上的音就是中央C,即C4。和高音谱号类似,低音谱号的圆心标记的是F3在谱中的位置,即第四线上。
四、和声
和声,是指由超过一个单音所组合而成的声音。你可能会发现,和声的定义与拍音的定义是非常相似的。的确如此,所有的拍音都是和声,但和声不一定会产生拍音。
首先,人耳可以听到的声波频率范围大约为20Hz到20000Hz,如果和声产生的频率超过这个范围,通常就不能称之为拍音了。其次,不同的乐器发出的单音进行叠加也可以称为和声,这也不是拍音。最后,拍音要求所有单音同时发出,而和声则无此要求,只要一个音在另一个音结束之前发出,它们交叠的部分就形成了和声。
在西方古典音乐理论中,和声主要研究两个单音构成的和声,三个或以上单音构成的和声一般称为和弦。我们先讨论和声。在一个纯八度范围内,两个单音的和声一共有12种,即与12种音程相对应。某些和声比较悦耳,而某些则比较难听,这究竟是为什么呢?
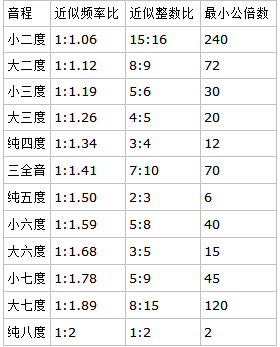
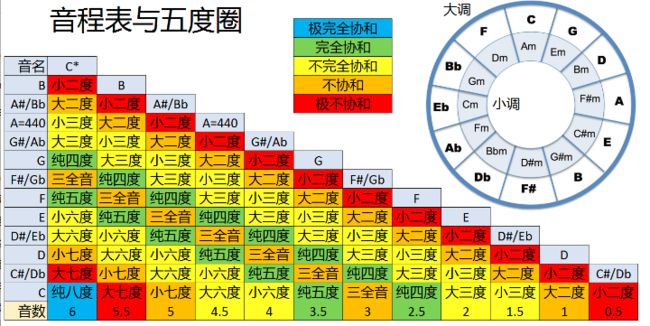
就是因为拍音!相邻两个音之间的频率比为2^(1/12)≈1.059463,我们将这个数记为p,那么各音程的频率比(即相距某个音程的低音比高音)可由其音数t按公式:1/(2t)^p算得。由于除纯八度外的所有音程的频率比均为无理数,因此他们的拍音的频率只能按他们频率的近似整数比来计算。接下来我们分别换算一下12个音程的频率比。
按近似整数比的最小公倍数排序,可以得到如下和声序列:【纯八度,纯五度,纯四度,大六度,大三度,小三度,小六度,小七度,三全音,大二度,大七度,小二度】。通过在钢琴上弹奏对比可知,越向左边的和声越“协和”,但也越空洞,就是好像只有一个音,不够饱满;越向右边的和声越“难听”,但也越饱满。
我们做一个实验来验证。比如C4和G4之间是完全协和的纯五度,他们的弦长比是3:2,最小公倍数是6,那么他们的拍音频率就是弦长为C4弦长2倍的弦所发出的声音的频率,显然就是C3的音。我们可以在在线钢琴上同时按下i(C4)和x(G4)键,然后试着同时按下i、x和q(C3)键听一听效果。可以感觉到C4和G4把C3增强了。同理,A6和B6这两个小二度音程的弦长比是16:15,最小公倍数240,拍音频率对应的音为B2,然而B2与A6和B6相隔太远了,我们无法听出拍音增强的效果。(拍频的计算)
和声理论已经发展为一门学科,若感兴趣可以阅读《和声学》。
五、和弦
和弦(念“xian”,不念“xuan”,通常发儿化音)原指弦线,在音乐理论里,是指组合在一起的两个或更多不同音高的音。在欧洲古典音乐及受其影响的音乐风格里,更多时候是指三个或以上的音高组合。和弦的组成音,可分开演奏,亦可同时演奏。分开演奏的,我们称为分解和弦。
和弦的结构类型很多,如果按照组成音的多寡来区分,和弦可以分为三和弦、七和弦及九和弦等。三和弦是由三个音组成,七和弦是由四个音组成,九和弦则由五个音组成。如果按照和弦组成音之间的音程结构来分类,又可分为大和弦、小和弦、增和弦和减和弦四种形态。
三和弦
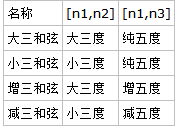
以任意一个音n1为基准,称为根音,向上三度得到n2,向上五度得到n3,这三个音的和弦称为三和弦。三和弦可以再分为大三和弦、小三和弦、增三和弦和减三和弦。这些三和弦的构成如下表所示:
上表中[n1,n2]表示从n1到n2的音程,[n1,n3]表示从n1到n3的音程。注意增五度就是小六度,减五度就是三全音,这是在上一讲中提到过的异名同音现象。接下来我们就用钢琴的音阶来举一些三和弦的例子。
C和E两键之间共有两个全音,因此是大三度,C和G是纯五度,那么C、E和G三个白键就构成了大三和弦,请在在线钢琴上试弹(对应键盘上的T、U和O)。C和Eb(E左边的黑键)是小三度,那么C、Eb和G三个键构成了小三和弦(在线钢琴的黑键可以用鼠标点)。同理可知:C、E和G#(G右边的黑键)构成增三和弦,C、Eb和和Gb(G左边的黑键)构成减三和弦。
通过比对我们可以听出,小三和弦的“协调”程度不如大三和弦,这一原因请朋友们用之前学习的和声理论进行分析。增三和弦和减三和弦的情况与之类似,朋友们可以自行推算所有增三和弦与减三和弦的音名。
七和弦
七和弦比三和弦多加一个音n4,它于n1的音程为七度。七和弦又分为:大小七和弦、大七和弦、小七和弦、小大七和弦、增七和弦、增七和弦和半减七和弦一共7种。
六、调式
调式:调式是若干个具有不同音高的音的集合,这些音互相之间具有某种特定的音程关系,并在调式中担任不同的角色。调式是决定音乐风格最重要的因素之一,调式和调性结合,决定了该段音乐所用的调。
现在最常使用的调式大体分为大调式和小调式两种,又细分为自然大调、旋律大调、和声大调、自然小调、旋律小调、和声小调等等,但无论哪种调式都具有7种不同的音,依次分别称为:主音、上主音、中音、下属音、属音、下中音和下主音,其中下主音有时也称作导音。这什么会有这样的名称呢?回顾我们上一讲提到的五度相生律就会明白:主音生属音,而中音位于主音和属音之间,主音下面是下主音、上面是上主音,属音下面是下属音,属音和下主音之间的另一个中音称为下中音。额,还是很麻烦呐,只能死记硬背了。。。不过还有另一种福音命名法:主音、I级音、II级音、III级音、IV级音、V级音、VI级音和VII级音(“福音”二字是我给起的,呵呵)。不同的调式规定了这些音之间不同的音程,但不规定音的具体音高。也就是说调式仍是建立在以十二平均律体系为基础的相对音高系统之上的。调式系统里最重要的是自然大调和自然小调,这两个自然调式一定要熟记,下面分别学习。
自然大调
自然大调是最常见的调式,大多数流行歌曲都采用自然大调。自然大调的规则是:除了“中音和下属音”,“下主音和主音”这两对音之间的音程是小二度之外,其他相邻两音之间都是大二度 (音数为1,即1个全音)。因此一个自然大调从主音开始依次往高的音程可以这样来记忆:“全全半全全全半”,这也就是著名的大调音阶。而一个主音到下一个主音之间的音程刚好是纯八度,也就是将一个主音当做1,计数到8的那个音与主音的音程。这下我们终于知道为什么叫做“纯八度”了,呵呵。
自然小调
自然小调是和自然大调同等重要的调式,在古典音乐中应用非常广泛。它的音阶为“全半全全半全全”。看起来与自然大调音阶只是相位不同而已,但实际上由于作曲时要先定调,就像写程序先设计框架结构一样。定了调之后就有了主音以及其它音的相对音高关系,而作曲时都要围绕主音进行。以主音为根音的三和弦称为主和弦,大调使用大三和弦,而小调使用小三和弦,因此听起来是有很大差异的。
小调音阶为【A3 B3 C4 D4 E4 F4 G4 A4】
其它小调式
大调一般只有一种,就是自然大调。苏联老毛子发明的什么和声大调、旋律大调都是瞎胡闹。但小调还分为和声小调、旋律小调和现代小调三种,但都比较少见,有些只在特别的音乐类型中出现,比如现代小调一般只出现在爵士乐中。
为什么小调会出现变种呢?这是因为小调有着天生的缺陷。自然大调的下主音和主音之间的音程是半音,即小二度,很好的体现了对主音的倾向。举例而言,从一个大调音阶中的B到C的过渡是非常自然和平缓的,这样作曲时就方便的使用跨越纯八度的和声。然而小调的下主音和主音之间的音程是全音,即大二度,欠缺了倾向主音的性质,因此人们就尝试将自然小调音阶的导音提升半音,这样就得到了和声小调音阶。旋律小调和现代小调就更加复杂一些,牵扯不同的上行音阶和下行音阶,这些过于专业的内容就不再赘述了。
音的倾向性排列(倾向于稳定):1 5 3(稳定音)6 2 4 7(不稳定音)
大小调关系
前面所说的绝对音名相同但相位不同的大小调称为关系调,比如降E大调(降E大调是指该调采用的主音为Eb)的关系小调叫做c小调,降E大调音阶是Eb、F、G、Ab、Bb、C、D,c小调的音阶是C、D、Eb、F、G、Ab、Bb,可以看出它们采用的音名都是相同的,但做了移相。因此从升降号上是无法区分大小调的,但是通过观察谱子里使用的主音就很容易区分了。现在朋友们的基础知识不够,等一下讲介绍了调性理论后,我们会来练习从谱子中看出调式与调性。
大调一直以来都是作曲家钟爱的调试,而相比之下小调的音乐就比较少了,古典音乐里二者还相差不多,但流行乐中的小调就少得多了。这主要是因为小调的歌唱性没有大调强,常用来表达负面的情感,比如悲伤、阴沉、恐怖等,在电影、游戏中的背景音乐中常可以听到。不过流行歌曲也是有一些的,比如《白桦林》、《爱的供养》、《伤心太平洋》等,国外的流行歌曲到是多一些,而且有人研究发现:从1960年代以来越来越多的流行歌曲是以小调作曲的。
七、调性
有了十二平均律,转调不再成为问题,因此人们就能够以不同的音为主音按大调式或小调式构造出不同的音阶,这些设定了主音的音阶序列就称为调性。先来研究大调式的所有调性。
我们已经学过大调的音程关系为“全全半全全全半”,那么从12音阶中的任意一个音作为主音都可以得到一个调性。
调性的名称就是主音的音名,12音阶中有7个音名是不带升降号的,因此以这些音为主音的调性的名称是统一的。然而还有5个音都具有两个音名,例如第2音可以用C#表示也可以用Db表示。这样一来调性的命名就变得混乱了。为了统一命名方式,人们规定这12个调性的名称分别为:{C, G, D, A, E, B, F#, Db, Ab, Eb, Bb, F},并规定以C、G、D、A、E、B、F#为主音的调性用升号#标记五线谱的升降,其它调性用降号b标记五线谱的升降。【在升号调时,音的表示要写升号:G D A E B F# C#。降号调:F Bb Eb Ab Db Gb Cb。】
首先我们很容易就可以做出C大调,因为以C为主音的7音阶都不带升降号,因此C大调谱是没有升降号的,见图
根据之前所学知识,我们很容易构造出其它大调,构造所有小调的原理也相同。这样我们就一共可以获得12个大调和12个小调。其中12个大调见图
由于Gb调中每个音符都降了半音,F#调中每个音符都升半音的本质是相同的,因此和它们是同一个调。此外,有些谱子会用7个降号来表示Cb大调,实际上C降半音就是B,那么Cb大调就是B大调。还有7用个升号表示C#大调,C升半音就是Db,因此C#大调就是Db大调。这样一来,Bb大调所有音升半音就得到了B大调,Eb大调所有音升半音就得到了E大调,F#大调所有音降半音就得到了F大调,其它的升降大调也是相同。大调确定了,关系小调也就可以确定了。为了便于记忆这24个调,有人发明了五度圈图示法。
关系小调:一个大调的关系小调是大调1级和弦的上方6级所形成的小调(相差4个半的音程)。关系大小调是指在音阶构成上共同音最多的两组调。比如说:C大调的音阶是:1、2、3、4、5、6、7、1(CDEFGABC)。a小调的音阶是:6、7、1、2、3、4、5、6(abcdefga)。
为什么C大调的关系小调为什么是A小调,而不是E小调呢:大小调体系中的功能性取决于主音与上方三度音的音程关系,大调为大三度,小调为小三度。那么,你就能想通为什么a小调要从6开始,因为6与上方的三度音1构成小调的功能性小三度音程。当然,这不是充分条件,3和上方的5也构成小三度,那为什么不从3开始呢?
大调的关系小调从下方三度(或上方六度)开始才符合同音列的条件,即C大调与a小调音阶为什么是一样的,如果从3开始音阶还能一样吗,C大调与a小调就是同音列的关系嘛,称关系大小调,享有共同的调式自然音。
在五度圈的最外圈是大调的12个调性,内圈是各大调对应的关系小调。顺时针相邻两个大调的主音相差五度,小调亦然。圈里面的数字是该调性的五线谱中升降号的数量。最顶上的C大调没有任何升降号,顺时针方向升号依次增多,逆时针方向降号依次增多。最下面的Gb调和F#调实际上是一个调,只是记谱不同而已,可使用6个降号表示,也可使用6个升号表示。
对于五度圈右边的每个升号大调,从F开始以逆时针方向数,到它前面的2格为止,都是它的音阶中要升半音的音符,例如E大调的音阶中F、C、G、D都升半音,对于B大调的音阶中,F、C、G、D、A都要升半音。对于左侧的降号大调,则是从B开始以逆时针方向数,到它正对面调都是它的音阶中要降半音的音符,例如Ab大调的音阶中B、E、A、D都要降半音,Db大调的音阶中B、E、A、D、G都要降半音。
五度圈还有一些规律要知道,从任何一个音开始逆时针数,第一个音与它的音数是2.5;顺时针数第一个是3.5。这个规律可以帮你用五度圈来推算音程。比如要求G到F#的音程,从五度圈可知F#是G顺时针方向第5个,(5*3.5)%6=5.5,即大七度。再看从F到Ab,是逆时针第3个,(3*2.5)%6=1.5,即小三度。
音程与音数的对应记忆起来稍难一些,但是也有技巧。音程口决是:“小大小大纯三纯,小大小大纯”。前7个从小二度开始,后5个从小六度开始。掰指头数一下这个音程排在总第几位,除以2就是它的音数。比如小七度排在第10位,音数就是5。
八、拍子、四分音符、小节
拍子是时间单位,如1分钟60拍,那一拍就是1s;如1分钟120拍,那一拍就是0.5s;
四分音符为一拍,则半分音符为2拍,全音符为4拍,八分音符为0.5拍;
3/4,表示四分音符为一拍,一个小节有3个四分音符;
原文链接:http://www.cnblogs.com/devymex/p/3385179.html