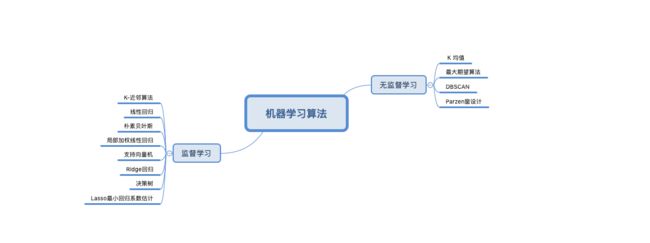
关键技术
特征: 比如鸟的体重、后背颜色等成为特征
机器学习的主要任务是分类
训练集: 用于训练机器学习算法的样本集合
目标变量: 机器学习算法的预测结果
机器学习算法通常都有两个独立的样本集: 训练数据和测试数据
主要任务
监督学习: 这类算法知道要预测什么,即目标变量的分类信息,比如回归和分类
如何选择合适的算法
选择算法需要考虑两个问题:
使用机器学习的目的,想要算法完成何种任务
如果要预测目标变量的值,则选择监督学习算法,否则选择无监督学习算法,
确定监督学习算法--> 进一步确定目标变量类型-->如果是离散类型可以选择分类算法,如果变量是连续型则需要选择回归算法- 需要收集和分析的数据是什么
对数据了解的越充分,越容易创建符合实际需求的应用程序
主要了解数据的以下特性:- 特征值是离散型变量还是连续型的变量
- 特征值是否存在缺失的值,何种原因造成缺失
- 数据中是否存在异常值
- 某个特征发生的频率如何
一般不存在最好的算法或者给出最好结果的算法,发展最好算法的关键环节是反复试错的迭代过程。
开发机器学习应用程序的步骤
- 收集数据 爬虫、RSS反馈、设备发送过来的实测数据
- 准备输入数据 得到数据,确保数据的格式符合要求
- 分析输入数据,此步骤主要是人工分析一起得到的数据,主要作用是确保数据集中没有垃圾数据
- 训练算法 将得到的格式化数据输入到算法,从中抽取知识和信息。无监督学习不需要训练算法,因为不存在目标变量值
- 测试算法 为了评估算法,必须测试算法工作的效果,不满意算法的输出结果,则可以回到第4步,改正加以测试。问题常常跟数据的收集和准备有关,这时,必须跳到第一步重新开始
- 使用算法 将机器学习算法转换为应用程序,检验是够可以在实际环境中工作,碰到新的数据问题,需要重新执行上述步骤
Numpy 函数库
引入Numpy库的所有模块
from numpy import *构造4 * 4 的随机数组
>>> random.rand( 4,4)
array([[0.55677722, 0.41866639, 0.760986 , 0.30543536],
[0.27857142, 0.9442911 , 0.66331734, 0.89142254],
[0.26417969, 0.16027738, 0.91083046, 0.86352393],
[0.87612067, 0.99348632, 0.2051467 , 0.76625919]])
使用mat()函数将数组转化为矩阵
randMat = mat(random.rand(4, 4))
矩阵求逆运算 .I 实现
>>> randMat.I
matrix([[-1.13842105, 1.53674477, -0.29591349, 0.365321 ],
[ 0.84070097, 0.31633497, -1.04074915, 0.48088582],
[ 2.5591936 , -0.04934141, 0.74581399, -1.97045228],
[-1.63020629, -0.51454446, 0.63813902, 1.36543634]])矩阵乘法运算,结果是单位矩阵
randMat * invRandMat
matrix([[ 1.00000000e+00, 5.40651457e-17, 6.63615816e-17,
6.88499287e-17],
[-4.86799869e-17, 1.00000000e+00, -6.59178291e-17,
-3.37699800e-17],
[ 1.09568983e-16, -1.86950226e-16, 1.00000000e+00,
3.04480630e-17],
[ 8.26615040e-17, -5.03584922e-17, 2.16866473e-16,
1.00000000e+00]])单位矩阵计算误差 eye(4) 创建4 * 4 的单位矩阵
>>> myEye = randMat * invRandMat
>>> myEye - eye(4)
matrix([[ 2.22044605e-16, 5.40651457e-17, 6.63615816e-17,
6.88499287e-17],
[-4.86799869e-17, -1.11022302e-16, -6.59178291e-17,
-3.37699800e-17],
[ 1.09568983e-16, -1.86950226e-16, 0.00000000e+00,
3.04480630e-17],
[ 8.26615040e-17, -5.03584922e-17, 2.16866473e-16,
0.00000000e+00]])