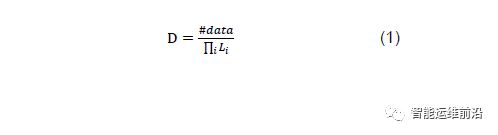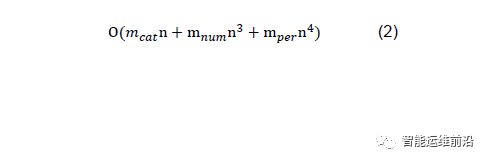AIOps从运维到运营:多维数据热点发现算法
原创: 邹磊 张明
简介
本文介绍一种多维数据热点发现的AIOps算法,既可应用于运维, 也可以应用于运营,都是Ops (Operations)。该工作发表于《小型微型计算机系统》。
该方法通过对多维数据进行聚类,找出数据聚集的区域,并通过特征取值组合(例如{时间∈[18,24],所在城市∈[北京,深圳,上海],网络延迟<30ms})将其表示出来。本文将数据聚集的区域称为数据热点,数据热点可以作为多维数据的一种可视化方法。
作者|邹磊 张明
编辑|Vicky
背景
用户数据分析是企业优化服务质量、提升用户体验的重要一环,常用的用户数据分析方法包括细分分析、对比分析、漏斗分析、同期群分析、聚类分析、AB测试、埋点分析、来源分析、用户分析、表单分析等,而热点发现是用户数据分析中没有使用的方法。热点发现的概念大家在生活中会经常接触,例如微博热搜、百度的搜索热点等,这些热点发现的工作本质上都是对大量的文本数据进行挖掘,找出这些文本数据聚集的区域,即热搜、热点、主流观点等。用户数据通常组织为多维数据的形式,针对文本数据进行的热点发现工作无法直接应用于多维数据。
多维数据通常包含多个与目标事件相关的特征,这些特征可以是用户的手机品牌、使用的服务类型、事件发生的时间、用户的地理位置、用户的网络延迟、软件版本、服务器负载、用户年龄等,每次目标事件发生都对应一条多维数据。例如图 1所示,该多维数据包含5个特征,并且展示了7条数据作为示例。
图 1多维数据示例
如果把多维数据的每一个特征都看作一个维度,那么多维数据就是分布于由各个特征的取值范围构成的特征空间中的数据。例如图 2所示,在由时间、网络延迟和所在城市三个特征构成的特征空间中,每个黑色方格都是一条数据,白色方格表示该处没有数据。多维数据的热点发现希望能够找出图中数据集中的两个热点区域(图中的虚线处),并以特征取值组合{时间∈[18,24],所在城市∈[北京,深圳,上海],网络延迟<30ms}和{时间∈[6,9]}将这两个热点区域的信息呈现给数据分析人员,特征取值组合通过限定一个或者多个特征的取值范围来表示数据的取值范围。实际的特征空间通常会超过三维,但是受限于图片的表达能力,在这里仅以三维特征空间作为例子。
图 2多维数据聚集区域示例
术语定义
热点定义:热点是指特征空间中的数据区域,其数据密度D>= Dthr,并且数据量Q>=Qthr。Dthr和Qthr为常数阈值,其取值根据具体应用由专家根据相关领域的专业知识选取。
数据密度定义:用于描述特征取值组合的数据集中程度的数据密度D的计算方式为
其中#data为该特征取值组合覆盖的数据数量;Li为该特征取值组合所确定的区域中特征i 的长度。
多维数据热点发现算法介绍
1. 基本思想
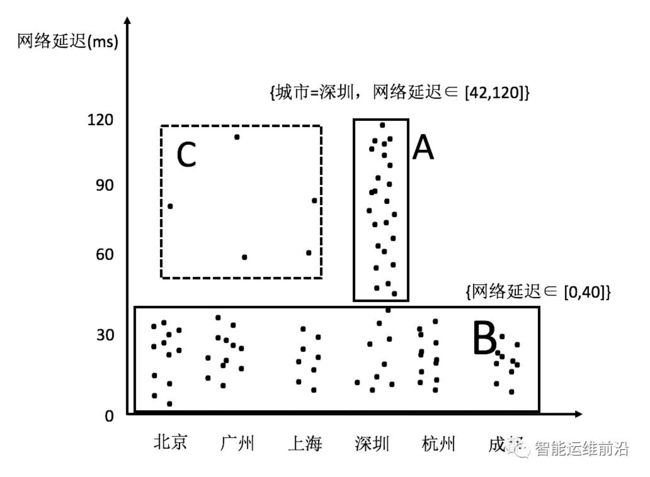
图 3热点发现算法基本思路示意图
本文使用聚类方法来解决多维数据的热点发现问题。例如图 3中的二维数据所示,其中的黑色点就是业务数据,数据集中分布在两片区域A和B中,区域C的数据则非常的稀疏。根据前面提到的需求,理想的情况是能够找出表示A和B两个区域的特征取值组合。为了实现这个目标,首先对数据进行聚类,在数据被聚成A,B和C三个类之后,再用刚好能够覆盖类中所有数据的特征取值的组合来界定每个类的边界。描述类A和类B边界的特征取值组合就是多维数据热点发现希望找到的结果。
2. 聚类算法选择
CLTree的聚类结果的边界整齐,可以直接用特征的取值组合进行表示,并且不需要预先输入需要将数据分成多少类,CLTree会根据数据的特点决定聚类结果中类的数目,因此本文选择CLTree作为基线算法。但是CLTree仅支持处理数值型特征、处理具有周期性的数值型特征效果不好,并且计算效率低。本文创新设计的CLTree+算法有效解决了CLTree的上述缺点。
CLTree+ 相对于 CLTree 进行了如下三点改进:
• 通过剪枝提升了聚类的计算效率。
• 增加对类别型特征的聚类支持。
• 提升了具有周期性特征的数值型特征的聚类效果。
3. 数据热点获取
CLTree+是沿着数据的整齐边界分裂数据的,因此CLTree+的聚类结果能够天然地用特征取值的组合来表示。从根结点到该叶结点的分裂路径即一系列特征取值条件的组合就可以表示该类。
本文以整体数据的密度Dglob作为基准线,并为所有类计算其数据密度与Dglob的比值。CLTree+的聚类结果中数据密度大于Dglob的类即可视作热点。用户在实际使用该算法时可以根据实际情况选择密度最大的若干个类作为数据热点。
4. 算法时间复杂度分析
对于类别型特征,CLTree+采用one-against-others二分裂,只需要遍历O(n)个分裂点,并且不需要对数据进行排序,处理每个特征时只需要遍历一次数据。只包含类别型特征的CLTree+的时间复杂度为O(mn)。
对于周期型特征,CLTree+将其转换成数值型特征进行处理,相当于多了n倍特征,只包含周期型特征的CLTree+的时间复杂度为O(mn4)。
对于含有mnum个数值型特征,mcat个类别型特征,mper个周期型特征的数据,CLTree+的时间复杂度为:
实验与结果分析
1. 实验数据介绍
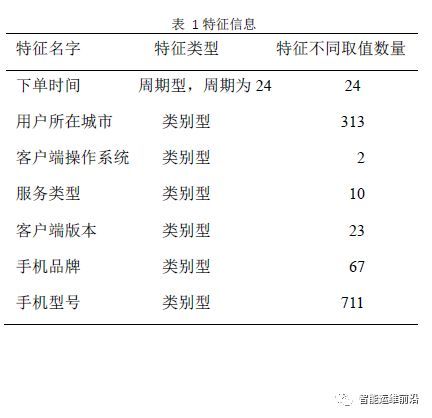
本次实验使用的业务数据为国内一家移动出行公司的订单数据,被使用的数据量已经经过了采样,采样之后的数据量约为10万条。每条业务数据都包含了7个特征,各个特征的信息如表 1所示:
所有实验数据都进行了脱敏,时间特征的取值加入了一定小时数的时间偏移,其它类别型特征的取值都用编号代替。
2. 实验结果介绍
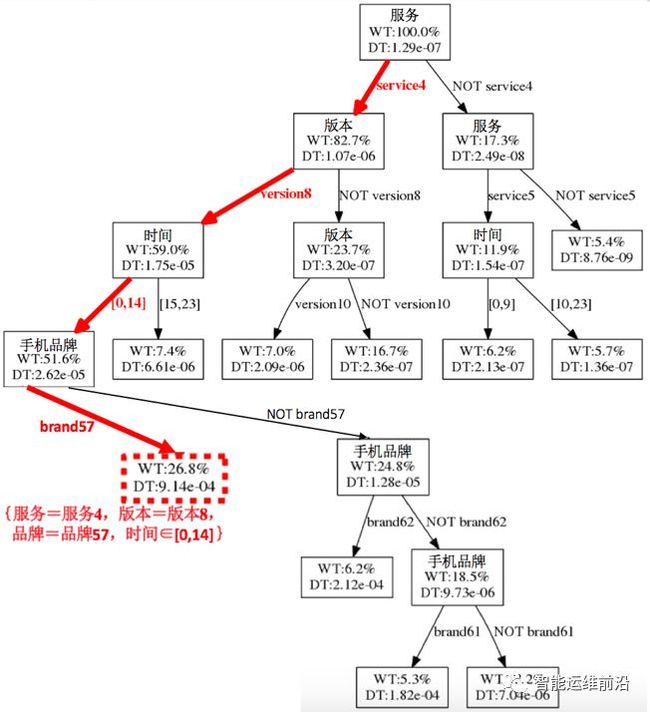
将CLTree+应用到实验数据后得到如图 5所示的聚类树。算法输入参数叶结点最小数据量定为总数据量的5%,最小信息熵增益定为0.01。图 5记录了数据分裂的详细过程,图中每一个结点都表示数据分裂过程中的一个数据子集,最上层的根结点表示整体数据集。如果一个结点有子结点,则说明该数据集继续进行了分裂。结点中的特征名表示该数据集在该特征上根据一定的条件进行分裂,而连接结点的边上的信息表示分裂该数据集的条件。例如,根结点表示的数据根据服务的取值被分成两个子数据集,一个子数据集中数据的服务特征取值均为服务4,另外一个子数据集中数据的服务特征取值均为非服务4。从根结点到目标结点的路径上的一系列分裂条件就构成了表示目标结点的特征取值组合,例如图 5中的红色结点(虚线框)所示,从根结点到该结点的4个用红色箭头(粗箭头)表示的分裂条件就构成了表示该结点的特征取值组合{服务=服务4,版本=版本8,品牌=品牌57,时间∈[0,15)}。所有的叶子节点构成了最终的聚类结果。
图 5移动出行公司订单数据建立的CLTree+
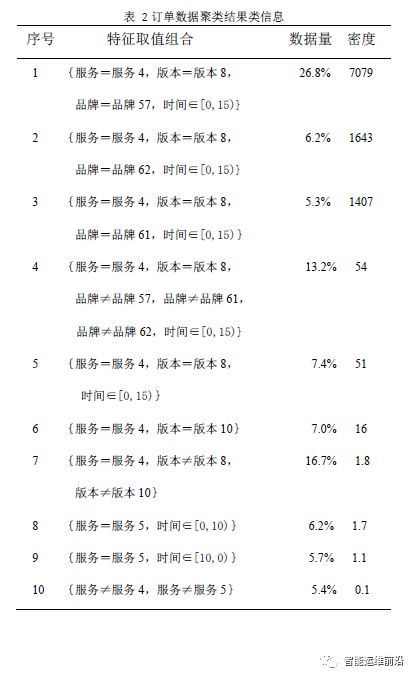
表 2按数据密度与整体数据的数据密度比值降序的方式展示了聚类结果中所有的类。最后的聚类结果中能够出现较多的像类1这样的数据覆盖量大且数据密度较高的类是比较好的结果。
3. 效果评估
并没有一个通用的指标可以用于评价多维数据热点发现的结果,并且由于所有可能的特征取值组合数量巨大,因此也无法通过遍历并对比所有可能的特征取值组合来评价热点发现结果。目前主要依赖该移动出行公司的数据专家结合具体的专业知识对结果进行评估。通过对聚类结果的认真评估,数据专家一致认为热点发现的结果非常符合他们的历史经验,结果比较理想。
4. 性能评估
用于测试实验程序运行速度的硬件环境为一台搭载英特尔至强E5-2620,2.4GHz,64GB内存的服务器,操作系统为Debian 8.7,所使用的编程语言为Python2.7。实验程序为一个单机版单线程程序,并没有使用任何集群技术或者多线程技术。
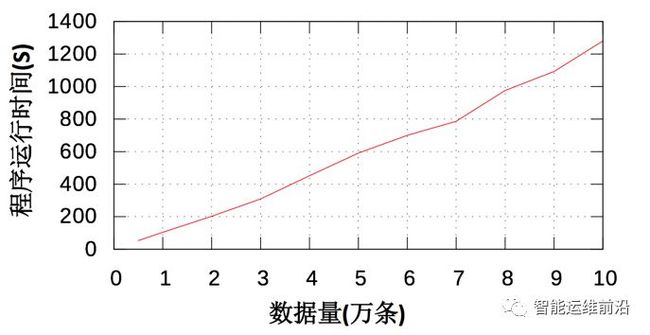
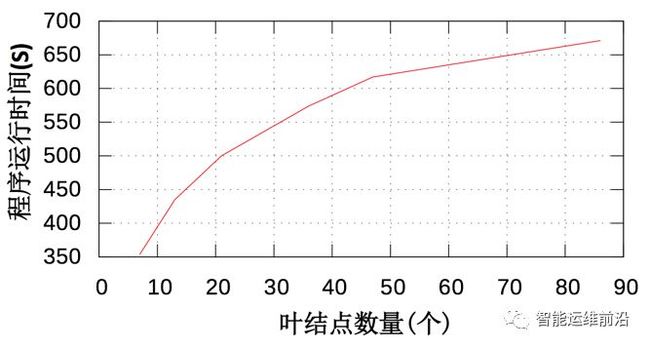
下面给出了将CLTree+应用于某大型互联网公司的用户数据时得到的数据量、每条数据包含的特征、CLTree+的分裂深度对程序速度的影响。所有程序运行速度的数据都是运行5次程序取平均值得到的。图 10展示了数据量对程序运行速度的影响,从图中可以看出程序的运行时间随着数据量的增加基本上是呈线性增长,这是因为实验数据中的特征除了时间以外全部为类别型特征。图 11展示了决策树分裂深度对程序速度的影响。从图中可以看出程序的运行时间随着叶结点数量的增加而增加,但是增长得越来越慢,基本呈对数曲线关系。出现这种情况是因为随着数据的分裂,子数据集中的数据量会越来越少。
图 10数据量对程序运行速度的影响
图 11决策树分裂深度对程序速度的影响
结语
本文介绍了一种多维数据热点发现算法,通过CLTree+对数据进行聚类找出数据聚集的热点区域。该算法应用于真实用户数据,取得了很好的效果。
邹磊,朱晶,聂晓辉,苏亚,裴丹,孙宇,《基于聚类的多维数据热点发现算法》,《小型微型计算机系统》