数据结构和算法
- 通用数据结构:数组、链表、树、哈希表
- 专用数据结构:栈、队列、优先级队列
- 排序:插入排序、希尔排序、快速排序、归并排序、堆排序
- 图:邻接矩阵、邻接表
- 外部存储:顺序存储、索引文件、B-树、哈希方法
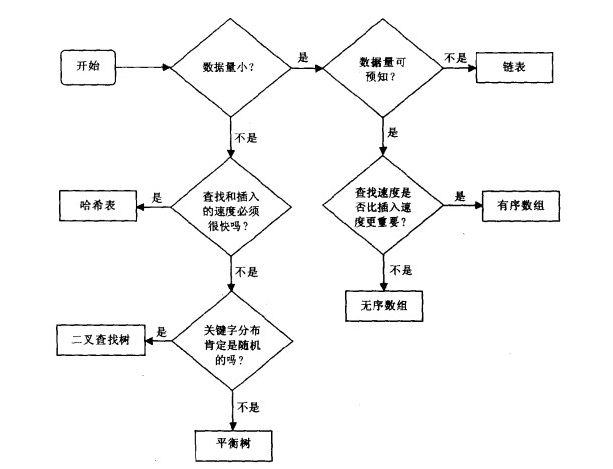
通用数据结构
通用的数据结构:它们通过关键字的值来存储并查找数据,这一点在通用数据库程序中常见到(栈等特殊结构正好相反,它们只允许存取一定的数据项)。
速度与算法
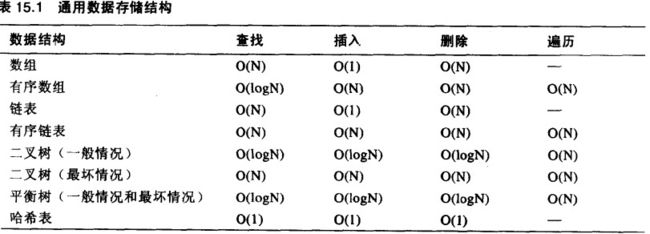
通用数据结构可以完全按照速度的快慢来分类:数组和链表是最慢的,树相对较快,哈希表是最快的。
但是不要有这样的结论:使用最快的结构永远是最好的方案。这些最快的结构也有缺陷。
- 首先,它们的程序在不同程度上比数组和链表的复杂;
- 其次,哈希表要求预先知道要存储多少数据,数据对存储空间的利用率也不是非常高。普通的二叉树对顺序的数据来说,会变成缓慢的O(N)级操作,而平衡树虽然避免了上述的问题,但是它的程序编制起来却比较困难。
处理器速度因素
快速的结构都有缺陷,而计算机的另一个发展因素却能使低速的结构更加具有吸引力。新计算机的CPU和存取速度每一年都有提升。Moore定律声明了CPU的速度每18个月翻一倍。这造成了早期计算机和现代应用的计算机在性能方面的惊人差异,而且目前没有任何理由能忍我这个增长速度会减慢。
几年前一台电脑可以在一个可接受的时间内处理100个对象的数组,而现在的计算机则快多了,因此可以在同样的时间里处理含有10000个对象的数组。
请从简单数据结构入手考虑:除非它们明显是太慢了,否则就用数组或链表编写程序,看看结构究竟怎样。
如果能在一个可接受的时间内运行完毕,那么就采用它,不必再找别的。没有人会留意用的是数组或别的什么结构,为什么一定要拼命地写出一个平衡树的算法?甚至必须面对成千上万、百万的数据项进行操作时,不妨先看一看数组或链表处理表现的情况,这也还是值得的。
只有在实验中发现这些简单结构的性能太慢时,才回过头来采用哪些更加复杂的数据结构。
数组
当存储和操作数据时,在大多数情况下数组是首先应该考虑的结构,数组在下列情况下很有用:
数据量较小
数据量的大小事先可预测(如果存储空间足够大的话,可以放松该条件,创建一个足够大的数组来应付所有可以预见的数据输入)
如果插入速度很重要的话,使用无序数组,如果查找速度很重要的话,使用有序数组,并用二分查找
数组元素的删除总是很慢,这是由于未来填充空出来的单元,平均半数以上的数组元素要被移动
在有序数组中的遍历是很快的,而在无序数组不支持这种功能。
向量类是一种当数据太满时可自己扩展空间的数组,可应用于数据量不可预知,在向量扩充时,将旧的数据拷入一个新的空间中会造成周期性暂停。
链表
*如果需要存储的数据量不能预知或者需要频繁地插入删除数据元素时,考虑使用链表。
当有新的元素加入时,链表就开辟新的所需要的空间,所以它甚至可以占满全部可用的内存;在删除过程中,没必要像数组那样填补"空白"
在一个无序的链表中,插入是相当快的,查找和删除却很慢,因此,与数组一样,链表最好也应用于数据量相对较小的情况。
对于编程而言,链表比数组复杂,但它比树或哈希表简单。
二叉搜索树
当确认数组和链表过慢时,二叉搜索树是最先应该考虑的结果,树可以提供快速的O(logN)级的插入、查找和删除。遍历的时间复杂度是O(N)级的,这是任何数据结构遍历的最大值(根据定义,必须访问所有的数据)。对于遍历一定范围内的数据可以很快得出访问数据的最大值或最小值。
对于程序来说,不平衡的二叉搜索树要比平衡的二叉树简单得多,但不幸的是,有序数据能将它的性能降至O(N)级,然而如果可以保证数据是随机进入的,就不需要用平衡。
平衡树
在众多平衡树中,我们讨论了红黑树和2-3-4树,它们都是平衡树,并且无论输入数据是否有序,它们都能保证性能为O(logN)。然而对于实现来说,平衡树是很复杂的,特别是红黑树。如果利用树的商用类,可以降低复杂性。
哈希表
哈希表在数据存储结构中速度最快,这使它成为计算机而不是人与数据交互时的必需。哈希表通常用于拼写检查器和作为计算机语言编译器的符号表,这些应用中,程序必须在几分之一秒的时间里检查上千的词或符号。
哈希表对插入的顺序并不敏感,因此可以取代平衡树。但是哈希表的编程比平衡树简单多了。
哈希表需要有额外的存储空间,尤其是对于开放地址法,因为哈希表用数组作为基本结构,所以,必须预先精确地知道待存储的数据量。
用链地址法处理冲突的哈希表是最健壮的实现方法,若能预先精确地知道数据量,在这种情况下,用开放地址法编程最简单,因为不需要用到链表类。
哈希表并不能提供任何形式的有序遍历,或对最大值、最小值进行存取,如果这些功能很重要,使用二叉树更好些。
通用数据存储结构的比较
专用数据结构
专用数据结构有栈、队列和优先级队列。
这些结构不是为了用户可访问的数据库而建立的,通常用它们在程序中辅助实现一些算法。
栈、队列和优先级队列是抽象数据类型,它们由一些更加基础的数据结构如数组、链表或堆来实现。
这些ADT只提供给用户间的的接口,一般仅允许插入和访问或者删除一个数据项。这些数据项是:
专用结构的比较:
排序
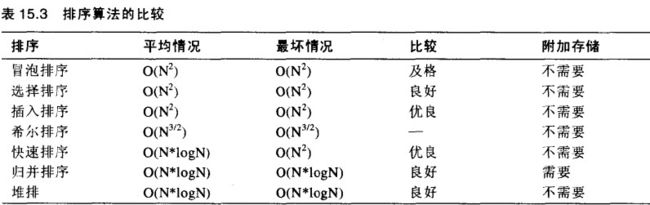
当选择数据结构时,可以先尝试一种较慢但简单的排序,例如插入排序。如果采用了这些方法,现代计算机的快速处理速度也有可能在恰当的时间内将较大的数据量排序。
插入排序对几乎已排好的文件也很有效,如果没有太多的元素处于乱序的位置上,操作的时间复杂度大约在O(N)级,这通常发生在往一个已排好序的文件中插入一些新的数据元素的情况。
如果插入排序显得太慢,下一步可以尝试希尔排序,它很容易实现,并且使用起来不会因为条件不同而性能变化差距太大:Sedgewick估计它的数据量为5000以下时很有用。
只有当希尔排序变得很慢时,你才应该使用那些更复杂但更快速的排序方法:归并排序、堆排序或快速排序。归并排序需要辅助存储空间,堆排序需要有一个堆的数据结构,前两者都比快速排序在某些程度上慢,所以当需要最短的排序时间时经常选择快速排序。
然而,快速排序在处理非随机性能数据时性能不大可靠,因为那时它的速度有可能退化至O(N^2)级。
对那些有可能是非随机性的数据来说,堆排序更加可靠,当快速排序没有被正确地实现时,它会产生微小偏差,在代码中细小的错误会使它对按某些顺序排列的数据无能为力,而诊断这种情况又相当难。
下面是几种排序算法的时间复杂度级别:
原文出处