通俗理解HMM与CRF

什么是HMM

隐马尔可夫模型HMM是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别,简言之，HMM是用来描述隐含未知参数的统计模型。

基本概念

可见状态链、隐含状态链

1.png

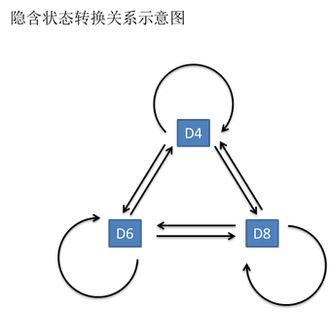
有三个骰子D4(正四面体骰子，四个面点数为1、2、3、4)、D6、D8，掷骰子10次得到1 6 3 5 2 7 3 5 2 4，这串数字叫做可见状态链。
但是在隐马尔可夫模型中，还有一串隐含状态链。本例中隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8

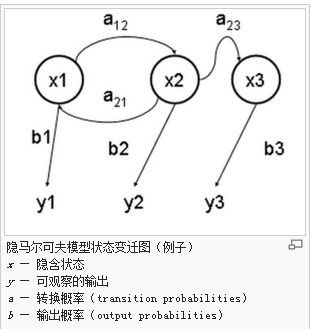
转换概率(transition probability):
一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态(骰子)之间存在转换概率。D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。其实是可以随意设定转换概率的。比如可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

2.png
输出或者发射概率(emission probability)
同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。
总结
可见状态链：掷骰子10次得到1 6 3 5 2 7 3 5 2 4点数序列
隐含状态链：使用骰子序列D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
转换概率：隐含状态(骰子)之间的概率，比如D6的下一个状态是D4，D6，D8的概率都是1/3
发射概率：隐含状态和可见状态之间概率，比如D6产生1的发射概率是1/6

3.jpg

任何一个HMM都可以通过下列五元组来描述
param obs: 观测序列
param states: 隐状态
param start_p: 初始概率（隐状态）
param trans_p: 转移概率（隐状态）
param emit_p: 发射概率（隐状态表现为显状态的概率）
隐态决定观察态，下一个隐态依赖于上一个隐态
经典的例子
小美每天根据天气{下雨，天晴}决定当天的活动{公园散步,购物,清理房间}中的一种，根据她朋友圈“我前天公园散步、昨天购物、今天清理房间了！”推断这三天的天气。

states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

在这个例子里，显状态是活动，隐状态是天气。观测序列就是这三天的活动序列，隐含序列是这三天的天气序列，转换概率是每天天气对后一天的影响概率，发射概率是每天天气对当天活动的影响概率。

【附CRF直观理解】：如果将lstm接全连接层的结果作为发射概率，CRF的作用就是通过统计label直接的转移概率对结果lstm的结果加以限制，比如I这个标签后面不能接O，B后面不能接B，如果没有CRF，光靠lstm就做不到这点，这样条件随机场的叫法就很好理解了。最后的score的计算就将发射概率和转移概率相加就ok了。

HMM的两个重要假设：

首先，一个隐马尔可夫模型有两个序列：
观测序列(可见序列)：L1、L2、L3、L4，状态序列(隐藏状态序列)：S1、S2、S3、S4，

齐次马尔可夫性假设
即任意时刻的隐藏状态只依赖于它前一个隐藏状态，即：t时刻的状态S2只依赖于前一时刻的状态S1
观测独立性假设
即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态，即：t时刻的观测L2(活动、做什么事)只依赖于该时刻的状态S2

HMM模型三个典型问题和算法

对于HMM来说，如果提前知道所有隐含状态之间的转换概率，和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候呢，往往是缺失了一部分信息的，由此产生三类问题：

预测解码问题，即求解最可能的隐状态序列
知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。
这类问题通常用维特比算法解决。维特比算法就是求解HMM上的最短路径（-log(prob)，也即是最大概率）的算法。
评估观察序列概率
还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。
这个问题的求解需要用到前向后向算法，这个问题是HMM模型三个问题中最简单的。
模型参数学习问题
知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。
这类问题需要用到基于EM算法的鲍姆-韦尔奇算法，是HMM模型三个问题中最复杂的。很多时候我们只有可见结果，不知道HMM模型里的参数，我们需要从可见结果估计出这些参数，这是建模的一个必要步骤。

维特比算法求解最可能的隐状态序列

首先，如果我们只掷一次骰子：看到结果为1。对应的最大概率骰子序列就是D4，因为D4产生1的概率是1/4，高于1/6和1/8。
把这个情况拓展，我们掷两次骰子：结果为1，6。这时我们要分别计算第二个骰子是D6，D4，D8的最大概率。显然，要取到最大概率，第一个骰子必须为D4。我们发现，第二个骰子取到D6的概率最大。而使这个概率最大时，第一个骰子为D4。所以最大概率骰子序列就是D4 D6。
继续拓展，我们掷三次骰子：结果为1，6，3。同样，我们计算第三个骰子分别是D6，D4，D8的最大概率。我们再次发现，要取到最大概率，第二个骰子必须为D6。我们发现，第三个骰子取到D4的概率最大。而使这个概率最大时，第二个骰子为D6，第一个骰子为D4。所以最大概率骰子序列就是D4 D6 D4。
总结
首先，不管序列多长，要从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率。然后，逐渐增加长度，每增加一次长度，重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了，重新计算的话其实不难。当我们算到最后一位时，就知道最后一位是哪个骰子的概率最大了。然后，我们要把对应这个最大概率的序列从后往前推出来。
维特比算法
首先你算出第一个状态取每个标签的概率，然后你再计算到第二个状态取每个标签得概率的最大值，这个最大值是指从状态一哪个标签转移到这个标签的概率最大，值是多少，并且记住这个转移（也就是上一个标签是啥）。然后你再计算第三个取哪个标签概率最大，取最大的话上一个标签应该是哪个。以此类推。整条链计算完之后，你就知道最后一个词去哪个标签最可能，以及去这个标签的话上一个状态的标签是什么、取上一个标签的话上上个状态的标签是什么，酱。这里我说的概率都是
exp里面的加权和，因为两个概率相乘其实就对应着两个加权和相加，其他部分都没有变。
与HMM区别
(1）HMM是假定满足HMM独立假设。CRF没有，所以CRF能容纳更多上下文信息。
(2）CRF计算的是全局最优解，不是局部最优值。
(3）CRF是给定观察序列的条件下，计算整个标记序列的联合概率。而HMM是给定当前状态，计算下一个状态。
(4）CRF比较依赖特征的选择和特征函数的格式，并且训练计算量大

7.CRF
不管这些照片之间的时间顺序，想办法训练出一个多元分类器。用一些打好标签的照片作为训练数据，训练出一个模型，直接根据照片的特征来分类。
乍一看可以！实际上忽略了这些照片之间的时间顺序这一重要信息，分类器会有缺陷的。在为一张照片分类时，我们必须将与它相邻的照片的标签信息考虑进来。

词性标注
给一个句子中的每个单词注明词性。如何评价一个标注序列靠谱不靠谱。比如动词后面还是动词就是一个特征函数，可以定义一个特征函数集合，用这个特征函数集合来为一个标注序列打分，并据此选出最靠谱的标注序列。
也就是说，每一个特征函数都可以用来为一个标注序列评分，把集合中所有特征函数对同一个标注序列的评分综合起来，就是这个标注序列最终的评分值。

3.PNG

4.PNG

定义好一组特征函数后，我们要给每个特征函数f_j赋予一个权重λ_j。现在，只要有一个句子s，有一个标注序列l，我们就可以利用前面定义的特征函数集来对l评分。上式中有两个求和，外面的求和用来求每一个特征函数f_j评分值的和，里面的求和用来求句子中每个位置的单词的的特征值的和。

为了建一个条件随机场，我们首先要定义一个特征函数集，每个特征函数都以整个句子s，当前位置i，位置i和i-1的标签为输入。然后为每一个特征函数赋予一个权重，然后针对每一个标注序列l，对所有的特征函数加权求和，必要的话，可以把求和的值转化为一个概率值。

CRF与HMM的比较

CRF比HMM要强大的多。对于词性标注问题，HMM模型也可以解决。HMM的思路是用生成办法，就是说，在已知要标注的句子s的情况下，去判断生成标注序列l的概率，如下所示：

pic7.PNG

这里：p(l_i|l_i-1)是转移概率，比如，l_i-1是介词，l_i是名词，此时的p表示介词后面的词是名词的概率。
p(w_i|l_i)表示发射概率（emission probability），比如l_i是名词，w_i是单词“ball”，此时的p表示在是名词的状态下，是单词“ball”的概率

1.CRF可以定义数量更多，种类更丰富的特征函数。HMM模型具有天然具有局部性，就是说，在HMM模型中，当前的单词只依赖于当前的标签，当前的标签只依赖于前一个标签。这样的局部性限制了HMM只能定义相应类型的特征函数，我们在上面也看到了。但是CRF却可以着眼于整个句子s定义更具有全局性的特征函数，如这个特征函数：

2.CRF可以使用任意的权重将对数HMM模型看做CRF时，特征函数的权重由于是log形式的概率，所以都是小于等于0的，而且概率还要满足相应的限制，如，。但在CRF中，每个特征函数的权重可以是任意值，没有这些限制。

3.HMM只是针对有向图来的，而CRF针对无向图

原文链接：
一文搞懂HMM https://www.cnblogs.com/skyme/p/4651331.html
HMM详解 https://blog.csdn.net/weixin_41923961/article/details/82750687
CRF链接 https://www.jianshu.com/p/55755fc649b1
CRF总结 https://www.cnblogs.com/lijieqiong/p/6673692.html