数据结构与算法（十三）平衡二叉树之AVL树

本文主要包括以下内容：

1. 平衡二叉树的概念
2. AVL树
3. 插入操作保持AVL树的平衡
4. 删除操作保持AVL树的平衡

平衡二叉树的概念

为什么需要平衡二叉树？

通过前面的 二分搜索树(Binary Search Tree)和 BinarySearchTree的时间复杂度分析 的介绍我们知道，二分搜索树的性能跟树的高度(h)有关系

h 为二分搜索树的高度，那么高度 h 和二分搜索树节点数 n 的关系是什么呢？

分析下满的二叉树的情况就知道了节点数量和二叉树高度的的关系了:

层数	该层的节点数
0层	1
1层	2
2层	4
3层	8
4层	16
h-1层	2^(h-1)

那么一个h层的满二叉树总共有多少节点呢？就是每层的元素个数相加即可：

n = 2⁰⁺²1+2³⁺²4+...+2^(h-1) = 2^h - 1

用对数表示就是：h = log(n+1)

用大O表示法就是： O(h) = O(log n)

上面是基于 满二叉树 的情况，所以二分搜索树最好情况的时间复杂度为 O(log n)

但是根据二分搜索树的性质知道，在最坏的情况二分搜索树会退化成链表，那么二分搜索树的在最坏的情况的时间复杂度为 O(n).

二分搜索树的最好情况的 O(log n) 和 最坏情况的 O(n) 是个什么概念呢？下面用一个表格对比下：

对比下 n 和 log(n) 之间的差距

n	log(n)	差距
16	4	4 倍
1024	10	100倍
100w	20	5万倍

随着数量不断的加大，它们之间性能的差距不断的两极分化。

这个时候就需要一个能够平衡的二分搜索树，就算在最坏的情况也能保证二分搜索树的性能保持在 O(log n)

那么什么是平衡二叉树，平衡二叉树 也称 平衡二分搜索树（Balanced Binary Tree）是一种结构平衡的二分搜索树。

平衡二叉树由二分搜索树发展而来，在二分搜索树的基础上平衡二叉树需要满足两个条件：

1. 它的左右两个子树的高度差的绝对值不超过1
2. 左右两个子树都是一棵平衡二叉树

常见的平衡二叉搜索树有：

1. AVL树
2. 红黑树
3. Treap

下面我们介绍下出现最早的平衡二叉树 AVL树。

AVL树

AVL树 是由 G. M. Adelson-Velsky 和 E. M. Landis于1962年提出。AVL树是最早的平衡二叉树。

AVL树维护自身的平衡涉及到两个概念：

1. 节点的高度
2. 节点的平衡因子

节点的高度就是从根节点到该节点的边的总和

节点的 平衡因子 是左子树的高度减去它的右子树的高度

带有平衡因子1、0或 -1的节点被认为是平衡的，因为它的左右子树高度差不超过 1

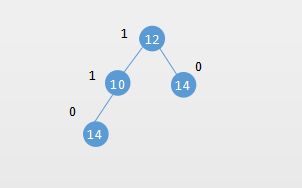
如下面一颗 AVL树：

这里写图片描述

上图的AVL树中，节点最大的平衡因子是1，所以它是一颗平衡二叉树。

一颗平衡二叉树的平衡性被打破肯定是在插入或者删除的时候，下面就来看如何在插入和删除的时候保持AVL树的平衡性。

插入操作保持AVL树的平衡

插入的元素在不平衡节点左侧的左侧，简称 LL

如下面一颗AVL树，在插入节点 5 后 节点 15 的平衡因子变成了 2，树的平衡性被打破：

这里写图片描述

这种情况我们称之为 插入的元素在不平衡节点左侧的左侧 简称 LL

遇到该情况需要对不平衡的节点进行右旋转：

这里写图片描述

通用情况如下：

这里写图片描述

右旋转代码：

private Node rotateRight(Node node) {
    Node nodeLeft = node.left;
    Node lRight = nodeLeft.right;
    //右旋转
    nodeLeft.right = node;
    node.left = lRight;

    //维护节点高度
    node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
    nodeLeft.height = 1 + Math.max(getHeight(nodeLeft.left), getHeight(nodeLeft.right));

    return nodeLeft;
}

插入的元素在不平衡节点右侧的右侧，简称 RR

这种情况也就是上一个情况的镜像。它需要对不平衡的节点向左旋转：

这里写图片描述

左旋转代码：

private Node rotateLeft(Node node) {
    Node nodeRight = node.right;
    Node rLeft = nodeRight.left;
    //左旋转
    nodeRight.left = node;
    node.right = rLeft;

    //维护节点高度
    node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
    nodeRight.height = 1 + Math.max(getHeight(nodeRight.left), getHeight(nodeRight.right));

    return nodeRight;
}

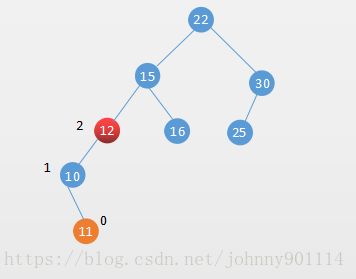
插入的元素在不平衡节点的左侧的右侧，简称 LR

插入的元素在不平衡节点的左侧的右侧，如下图所示：

这里写图片描述

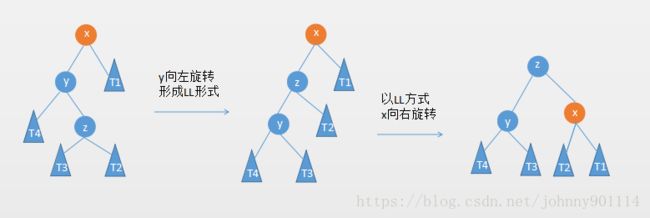
这个时候就不能单纯的对节点 12 右旋转，11和12都比10要大。这种情况需要两次旋转：

这里写图片描述

插入的元素在不平衡节点的右侧的左侧，简称 RL

插入的元素在不平衡节点的右侧的左侧，如下图所示：

这里写图片描述

插入操作维护AVL平衡性的相关代码：

public void add(K key, V value) {
    root = _add(root, key, value);
}
    
private Node _add(Node node, K key, V value) {
    if (node == null) {
        size++;
        return new Node<>(key, value);
    }

    if (key.compareTo(node.key) < 0)
        node.left = _add(node.left, key, value);
    else if (key.compareTo(node.key) > 0)
        node.right = _add(node.right, key, value);
    else //如果已经存在，修改对应value的值
        node.value = value;

    //维护node的高度
    //左右子树最高的高度+1
    node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

    //获取节点的平衡因子
    int balanceFactor = getBalanceFactor(node);

    // 右旋转
    // 左子树比右子树要高超过了1，说明当前节点的平衡被打破
    // 且新添加的节点是在左子树的左子树的左侧

    //LL
    if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
        return rotateRight(node);

    //RR
    if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
        return rotateLeft(node);

    //LR
    if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
        node.left = rotateLeft(node.left);//转化LL形式
        return rotateRight(node);
    }

    //RL
    if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
        node.right = rotateRight(node.right);//转化成RR
        return rotateLeft(node);
    }

    return node;
}

删除操作保持AVL树的平衡

删除操作和插入操作需要保持平衡的情况基本是一样的，代码如下所示：

private Node remove(Node node, K key) {
    if (node == null) {
        return null;
    }

    Node retNode = null;

    //如果要删除的节点小于当前节点，继续查询其左子树
    if (key.compareTo(node.key) < 0) {
        node.left = remove(node.left, key);
        retNode = node;
    }
    //如果要删除的节点大于当前节点，继续查询其右子树
    else if (key.compareTo(node.key) > 0) {
        node.right = remove(node.right, key);
        retNode = node;
    }

    //要删除的节点就是当前的节点
    else {
        //如果要删除节点的左子树为空
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            retNode = rightNode;
        }

        //如果要删除节点的右子树为空
        else if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            retNode = leftNode;
        }
        //=======如果要删除的节点左右子树都不为空
        else {
            //找到要删除节点的后继，也就是右子树的最小值
            Node successor = getMin(node.right);
            successor.right = remove(node.right, successor.key);
            successor.left = node.left;
            node.left = node.right = null;

            retNode = successor;
        }
    }

    //如果删除的节点是叶子节点
    if (retNode == null) {
        return null;
    }


    //得到retNode之后，维护平衡性

    //维护node的高度
    //左右子树最高的高度+1
    retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));

    //获取节点的平衡因子
    int balanceFactor = getBalanceFactor(retNode);

    // 右旋转
    // 左子树比右子树要高超过了1，说明当前节点的平衡被打破
    // 且新添加的节点是在左子树的左子树的左侧

    //LL
    if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
        return rotateRight(retNode);

    //RR
    if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
        return rotateLeft(retNode);

    //LR
    if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
        retNode.left = rotateLeft(retNode.left);//转化LL形式
        return rotateRight(retNode);
    }

    //RL
    if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
        retNode.right = rotateRight(retNode.right);//转化成RR
        return rotateLeft(retNode);
    }

    return retNode;
}

---

关注我 干货不错过

本文相关源代码github