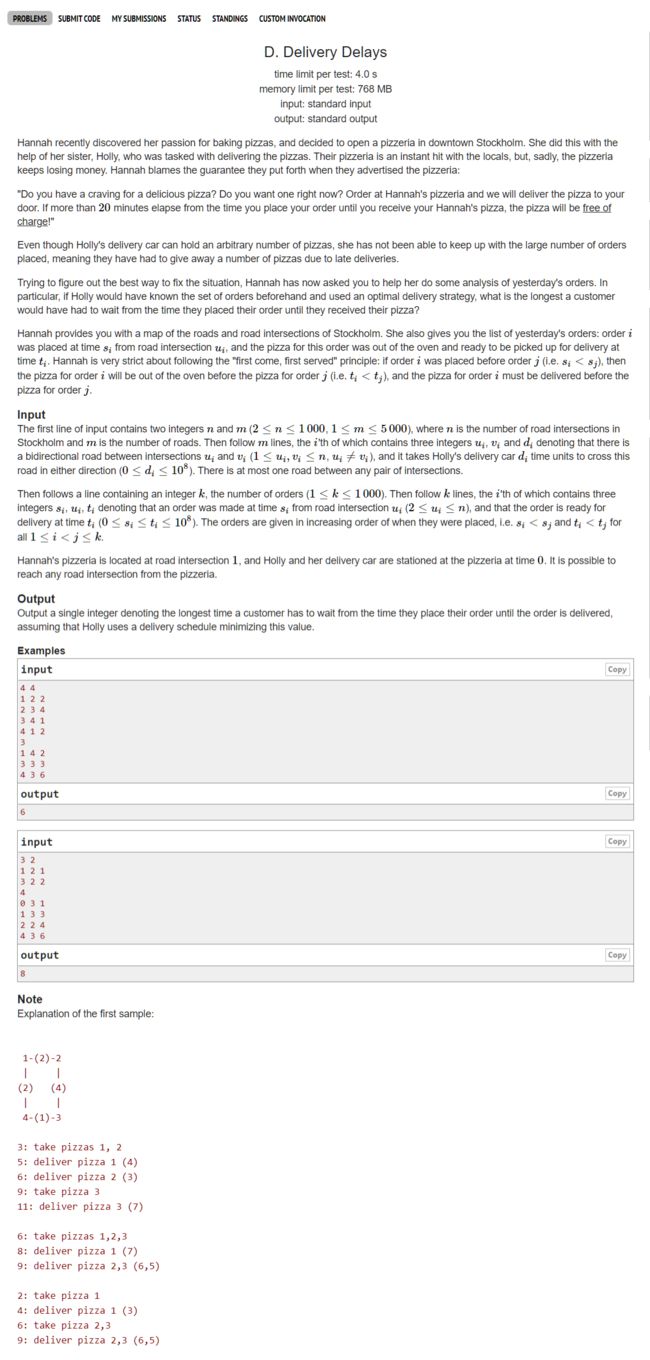
2018-2019 ACM-ICPC Nordic Collegiate Programming Contest (NCPC 2018)- D. Delivery Delays -二分+最短路+枚举
【Problem Description】
一座城市为无向图带权图,一号节点为披萨餐厅的位置,有\(k\)个人定披萨,按时间先后顺序给出定披萨的时间\(s_i\),地点\(u_i\)以及这个人的披萨在哪个时间做好\(t_i\)。问在所有配送方案中,所有人的等待时间的最大值最小是多少?配送顺序完全按照先来先服务的原则。
【Solution】
首先求\(n\)次\(Dijkstra\)求出任意两点间配送所需要的最短路程时间是多少。然后二分答案\(t\),即假定所有人的等待时间的最大值为\(t\),然后枚举验证即可。
因为配送顺序按照先来先服务的原则,所以不同方案间唯一的区别就是:从餐厅出发后连续配送多少个订单后回到餐厅。定义数组\(d[i]\)表示配送第\(i\)个人的订单,并回到餐厅需要的最短时间为\(d[i]\)。对于第\(i\)个订单,要么连续配送\(1,2,\dots,i\),要么连续配送\(2,3,\dots,i\),要么\(\dots\),要么直接配送\(i\),时间取最小值即可。所以直接\(O(n^2)\)枚举即可。
【Code】
#include
#include
#include
#include
#include
using namespace std;
#define int long long
#define maxn 1005
#define maxm 5005
#define INF 1e15
namespace Dijkstra{
struct node{
int v,w,next;
node(){}
node(int v,int w,int next=-1):v(v),w(w),next(next){}
bool operator <(const node&a)const{
return w>a.w;
}
}g[maxm<<1];
int head[maxn],cnt=0;
bool vis[maxn];
void init(){
memset(head,-1,sizeof(head));cnt=0;
}
void addedge(int u,int v,int w){
g[cnt]=node(v,w,head[u]);
head[u]=cnt++;
}
int dis[maxn][maxn];
void Run(int r,int n){
for(int i=0;i<=n;i++) dis[r][i]=INF;dis[r][r]=0;
memset(vis,0,sizeof(vis));
priority_queueq;
q.push({r,0});
while(!q.empty()){
node now=q.top();q.pop();
int u=now.v;
if(vis[u]) continue;
vis[u]=1;
for(int i=head[u];~i;i=g[i].next){
int v=g[i].v,w=g[i].w;
if(!vis[v]&&dis[r][u]+w>n>>m;
for(int i=1;i<=m;i++){
int u,v,w;cin>>u>>v>>w;
Dijkstra::addedge(u,v,w);
Dijkstra::addedge(v,u,w);
}
for(int i=1;i<=n;i++){
Dijkstra::Run(i,n); //求任意两个节点之间的最短路径
}
int q;cin>>q;
for(int i=1;i<=q;i++){
cin>>s[i]>>u[i]>>t[i];
}
int left=0,right=1e15,mid,ans=INF;
while(left<=right){ //二分答案
mid=(left+right)>>1;
if(check(mid,q)){
right=mid-1;
ans=min(ans,mid);
}else{
left=mid+1;
}
}
cout<