1 问题定义
1.1 问题描述
黄金点问题是一个由多个玩家参与的博弈游戏,每个回合,所有玩家各提交liang个0到99的数字,系统计算这些数字的平均值,并乘上0.618,返回结果作为这个回合的黄金点,复盘上一回合所有玩家的提交记录,和黄金点最接近的提交数的玩家得到N分(其中N为上一回合参加比赛的玩家人数),和黄金点最不接近的提交数的玩家扣掉2分。
1.2 我的猜测总结
- 实验发现,如果所有的同学采用的策略集合是简单action集合,不管使用的是Q-talbe,还是神经网络的DQN,最后结果的随机性都非常强,而且会输给一个策略非常简单的bot(采用的是固定的跟随策略,number1 为上一轮的黄金点,number2 为上一轮的黄金点乘上0.618),这个简单策略的bot在多次测试中都是遥遥领先的第一名,我们把它命名为superbot。
- 但如果有一位同学采用的是复杂策略(如在随机轮之后加一个“投机扰动”,一个number1 提交非常大的数字,另外一个number2 采用比上一个黄金点高一定数量来迎合number1),同时其他的bot都采用的是简单的actions集合(如取之前几轮的平均值,上一个黄金点乘上0.618,等)。在这种情况下,采用复杂策略的bot将会收到很好的成绩。
- 当有多个同学都采用了了复杂actions集合时,结果又会呈现很强的随机性,而且复杂策略bots多次输给了之前简单跟随的superbot。
1.3 问题难点
- 从我上面的实验结果和猜测看,这个游戏有一个很大的难点,我们不清楚其他的bot采用的是什么样的规则,我们也很难相应的设计我们的策略。
- 训练数据很少,之前我们组考虑使用之前的记录模拟训练,但是这样自己的结果不能被其他的bot 所感知到,和真实的比赛环境还是有一些出路的。于是验证想法的方式就只剩下了,自己写几个简单的bot一起开一个房间进行训练。但是这些简单的bot,并不能代表真实情况下所有同学的设计策略,就回到了上面一个难点了。
2 方法建模
2.1 方法的理论介绍
我和Xin Kang同学秉承着“多做实验少瞎猜”的精神,写了非常多个bots,它们主要用到了普通的q-learning,和DQN。下面我来给大家介绍一下这两个技术:
2.1.1. q-learning
q-learning 是一种基于q-table 记录智能体学习过程中积累的经验的RL 技术。 在智能体不断地与环境交互和成长的过程中,存在着三个我们需要注意的要素,state, ** action, reward**, 其中state 是指智能体的状态,action 是指智能体所采用的与环境相互作用的动作,reward 是指环境对于智能体的行动所产生的反馈,产生反馈的同时,智能体的状态会发生变化。用图表表示这个抽象的过程如下图所示:

其中的q-table 是一个数组矩阵,用来作为智能体的经验记忆,智能体对一个问题不断进步主要源自q-table 的更新。那么在智能体和环境交互的过程中,q-table是怎么更新的呢?
要知道q-table更新的,首先得知道q-table 的优化目标是什么。
q-table 是一种效用函数的表达形式,它的作用是,在输入当前state的情况下,输出采用各个action”将会“得到的效用或者说回报。当然这里说的”将会“,是根据以往经验预测的。那么根据Bellman 方程:
收获 \(G_{t}\) 为在一个马尔科夫奖励链上从t时刻开始往后所有的奖励的有衰减的收益总和。
\[ G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3\cdots}^{2}=\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \]
Bellman Equation 推导如下:
\[ \begin{aligned} Q(s) &=\mathbb{E}\left[G_{t} | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma G_{t+1} | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma Q\left(S_{t+1}\right) | S_{t}=s\right] \end{aligned} \]
由上面的推导可以看出,这个Q效用函数理论值或者说优化目标应该是 \(R_{t+1} + \gamma Q\left(s\_next\right)\)
有了优化目标,那么q-table(效用函数)的更新过程自然再清楚不过了:
\[ Q(s, a)=Q(s, a)+\alpha\left(Q_{target}(s, a)-Q(s, a)\right) \]
其中 \(Q_{target}(s, a) = R_{t+1} + \gamma max_{a}\left(Q\left(s\_next, a\right)\right)\)
2.1.2 DQN
理解了q-learning, 那么理解DQN 不难了,DQN 与前者不同之处在于,前者使用q-table 来表示效用函数,后者使用深度神经网络,每一轮设置
\[ loss = \left[Q_{target}\left(s\right) - Q\left(s\right)\right] ^{2} = \left[R_{t+1} + \gamma Q\left(s_{next}\right) - Q\left(s\right)\right] ^{2} \]
\[ \theta = argmin_{\theta} \left(loss\right) \]
即可。
2.2 我们使用的具体方法
我们采用了多种策略,
其中基于q-table 的 q-learning 的bots中
按照state 定义可分为:
- 前几次的黄金点 向下取整
- 前几次黄金点的$ log_{\frac{1}{0.618}}(goldennumber) $ 的向下取整
- 按照前十次黄金点 上升下降次数的编码 同 RLBotDemo 中对state 的定义
- 前一种定义上加上 最后一次 相对于倒数第10次 是上升还是下降
按照action 定义可分为:
- 直接产生0 到 99 的 整数,最后提交的number 是 action + random(0, 1)
- 直接产生0 到 7 的 整数, 最后提交的number 是 $ \frac{1}{0.618} ^{action + random(0, 1)} $
- 产生一个0 到 N - 1 的整数, 其中 N 为自己定义的 action 函数的种类
基于DQN 的 bot action 和上面的action 一致, 但是 state 是 前10次 黄金点(连续值)
和Hanyue Tu 等同学的实验结果显示,使用第四种state 定义, 第三种action 定义的 基于 q-table 的bot 结果最为稳定。
下面我画一下它的流程图:
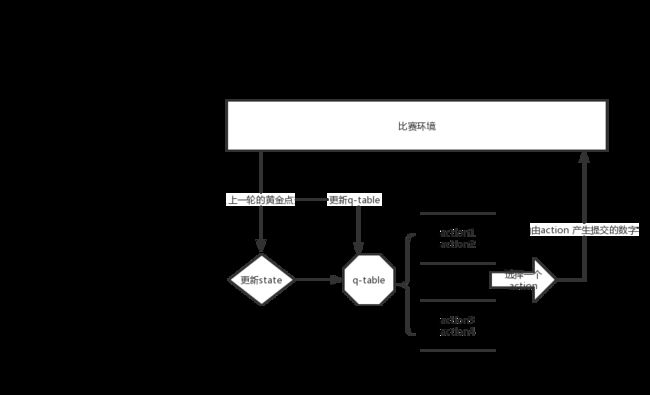
action定义:
action1:number1为前6个黄金点均值,number2为上一个黄金点加上前6轮之后黄金点的变化值。这个动作用于预测黄金点上下波动的情况。
action2:number1预测等比数列(number1=gArray[-1]/gArray[-2] * gArray[-1]),number2预测等差数列(number1=gArray[-1] - (gArray[-2]-gArray[-1]))。
action3:number1预测50,number2为上一个黄金点加上前6轮之后黄金点的变化值。
action4:number1为上一个黄金点,number2为上一个黄金点乘以0.618。
action5:number1为上一个黄金点,number2为前5个黄金点的平均值。
reward定义:
如果把每一轮的得分作为reward去更新Q表的话,由于大部分时候得分为0,所以Q表更新很慢。为了能够快速收敛,根据上一轮预测值里黄金点距离的排名,使用线性插值的方法得到一个相对得分作为reward。
其他细节:
在每一轮预测时,以概率p随机行动,以概率1-p选择期望回报最大的行动。游戏刚开始为了更够遍历Q表各个表项,p初始值为0.9,按照指数衰减,在1000轮后衰减到0.05,之后保持不变。
3 结果分析
比赛的结果当然不符合我们的预期,按照之前的实验结果,我们的bot 效果很好的, 可能是最好的几个bot 采用了(诸如一个number 提交一个大数, 另一个number相应提高抢第一这样的)复杂策略。
我们对于前1000次的成绩没有太在意,因为之前实验显示,我们的bot 确实是在1000轮之后才慢慢反超的,所以我们当时没有进行很大的修改。
我觉得三个数和两个数最大的区别是,三个数能够使用的复杂策略更多,由我文章最开始的经验总结来看,这样大家的bot 都趋向于使用复杂策略,这样比赛结果必将有不一样了。
我的队友Xin Kang 代码能力扎实, 非常认真负责,在Chao Li 老师发给我们demo之前,我们自己把网络接口啥的写了一遍,但是后来发现还是直接在Chao Li 老师的代码基础上改还是更方便。我们所有测试的bot 中最强的也是出自他手。
“三明治”法则?不存在的,Xin Kang 人非常好,有什么事情直接说就好了,嘻嘻