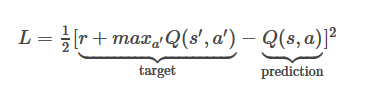文中使用的词汇及含义
agent: 在人工智能领域,一般用 Agent
来表示一个具备行为能力的物体,比如机器人,无人车,人等等。
reward: 反馈值,做出一个动作得到相应的回报,比如超级马里奥,跳一下吃到 dollar , 不错,得分,那么这一下操作得到的反馈就可以是正的,相反跳一下碰到蘑菇怪了,game over ,那这一下操作的反馈就可以是负的
action: 操作,行为,比如上面 reward 中提到的跳跃操作
强化学习
打砖块游戏对很多人来说并不陌生,一个不断运动的小球碰到玩家控制的横板会反弹回去,消除屏幕上方的砖块,然后得分。小球落地则游戏结束,所以需要尽可能移动横板保证小球不落地,同时让小球从多个角度弹回顶部消除更多的砖块来获取更高的分数。
现在目标是训练一个神经网络来玩这个游戏,屏幕图像作为输入,输出则是三种动作中的一种:左移,右移或者直接反弹。这可以看成一个分类问题 - 根据当前屏幕影像来选择将球拍左移,右移,还是直接反弹。听起来很简单?是的,但是这样就需要记录茫茫多的例子,尽可能学习到所有游戏可能的情况。当然我们可以用专门的游戏工具来记录所有游戏过程,下次玩的时候每到它记录过的情况,就会告诉我们该怎么操作。但这样一来就不是一个学习过程了。自我学习应该是做出选择,操作,得到反馈。是得分,还是 game over,接着根据反馈调整我们的方法,策略,指导下一次操作,不断积累经验,最终达到目标,获取高分。
这正是强化学习尝试解决的问题。它不完全等同于监督学习或非监督学习。监督学习中每个样本都有 一 一 对应的标签,非监督学习则没有。而强化学习具有一种特殊的“标签” - 反馈值(reward),随着游戏的进行,这些标签在时间维度上具有一定的联系。也正是基于这些 reward ,agent 才得以学会在各种情况下,执行相应的操作来达到目标。
虽然这些听起来很直观简单。但实际应用中却有很多挑战。例如当你击中一个砖块得到一分的时候,它可能与你在得到奖励之前所做的动作(移动横板)没有任何关系,因为之前你将横板移动到合适位置,等待接住小球的时候,该做的都做好了,剩下的只是慢慢看小球接触横板,反弹回顶部,击中砖块,得分,这期间所做的操作也许对这一刻的游戏结果没有任何影响,这就是牵扯到 信任分配问题(credit assignment problem),需要知道之前的行为中,哪些行为是直接影响了结果,使我们得分的,以及它们各自对结果的影响程度。我们要分配他们对结果影响的权重。
一旦你想出一个玩游戏的套路,你是满足于一直使用这个套路玩下去,还是想尝试能不能摸索出新的套路,得到更高的分数。比如玩这个打砖块游戏,如果通过观察发现,小球经常飞向左下角,我们可以直接把横板放在那个经常落下的位置,简单省事,这就是一个套路,运气好也许能拿个10分。但你只满足于这个10分吗?还是说你想要20分甚至更高。这就面临 是选择探索还是相信经验的两难问题(explore-exploit dilemma),是应该按套路走,还是去浪一下,万一有意外收获呢?
强化学习是我们(甚至所有动物)学习的重要模式。生活中,某个周六我们自发的修理了家里的草坪,做了点家务,得到父母的表扬,夸奖,孩子真懂事。在学校里,我们努力学习,获得了对应的学分。工作上,我们认真做事,拿到应有的薪水,这些都是得到反馈(reward),然后我们慢慢成长。在商业和人际关系,我们也经常需要对一些事物,资源,做合理的分配协调,也会不断的面临一些选择,而且有时候还会在选择上纠结。这也是研究强化学习这个模式的价值所在,而游戏,可以成为一个仿制了现实世界的沙盒,我们可以在其中不断模拟,不断探索。
马尔可夫决策过程
现在的问题是,如何将一个强化学习问题形式化,来方便我们推理。最常见的方法是把它看成马尔可夫决策过程。
假设你就是一个 agent,处在某一个环境中(比如上面的打砖块游戏),游戏环境处于某一种状态(横板所在的位置,小球的位置和移动方向,屏幕上方有多少砖块,都在什么位置等等),agent 去执行一些操作(比如向左或者向右移动横板)。这些操作可能会使我们得分,这个得分就是反馈(reward),分数可以是负数,比如小球没接住,也可以是0比如小球并未击中任何砖块。横板移动,小球运动,环境也就发生改变,处于一个新的状态,这个状态下 agent 又可以执行下一步操作,又得到一个反馈,以此类推。你如何判断什么样的情况该做什么样的操作,这就是你的套路。游戏下一步的状态也可能是随机的,比如小球没接住,游戏重新开始,小球会随机刷新在一个新的位置,你无法预料。
一系列的状态和行为,一个状态到另一个状态如何转变,构成了马尔可夫决策过程。在这个过程里的任何一个小节里(比如游戏里的一条命),都包含了小节内发生的所有情况,这就是一系列状态,也包含做出的一系列操作,以及相应的奖励情况:
这里 s[i] 代表状态,a[i] 代表行为,r[i+1]则是行为发生之后得到的反馈。这个小节直到 状态 s[n] 结束(比如屏幕显示游戏结束,一条命用完)。马尔可夫决策过程基于马尔可夫设定,即下一个可能的状态s[i+1]只取决于当前的状态si和行为ai,与之前的状态和行为都无关。
减少未来相同经验的指导价值
为了能在很长的一段时间内都有好的表现,我们不仅要考虑眼前的回报,还要考虑我们将来要得到的回报。我们该怎么做呢?
根据到马尔可夫决策过程,我们可以很容易地计算出一个小节的总回报:
考虑到这一点,从时间点 t 向后的总回报可以表达为:
但由于环境具有随机性,我们难以确定下一刻究竟会发生什么。如果我们下一次执行与上次相同的操作,得到了同样的反馈,随着时间的推移,次数的增加,就会产生选择上的分歧,经验很有可能会指导我们第 n 次依然作出相同的操作,但也许这时候环境却与之前都大不相同了。出于这个问题,每次这种情况形成的经验,它的指导价值应该被降低,打个折扣:
这里的 γ 就是这个折扣因素,在0到1之间,同样的情况在未来发生的次数越多,我们就会逐渐减少学习时对它的侧重。显而易见,未来步骤 t 中得到反馈值,可以用一次相同情况下的步骤 t+1 来表示:
当我们将 γ 设为0时,结果只取决于当下。我们想兼顾当下和未来,就应该赋予γ类似0.9这样的值。当然环境如果是不变的,并且同样的行为必然带来相同的反馈,γ 就可以设为1。
一个理想的 agent 应该能做出使未来回报最佳化的选择。
Q学习
在Q学习中,我们定义一个函数 Q(s, a),表示我们在状态 s 下执行动作 a ,未来能得到的最高分,然后持续优化这个函数使它能达到我们想要的效果。
可以这么理解,这个函数表示了游戏在状态 s 下,采取动作 a ,那么在游戏结束的时候,可能得到的最高分是多少。这叫做 Q函数,它代表了状态 s 下采取动作 a 这个选择的优劣。
这听起来可能有点奇怪,我们只知道当前的游戏状态,当前采取了一个动作,并不知道接下来会发生什么,那我们如何得知最后的游戏结果呢?我们的确无法得知,但这里作为一个理论假设,我们姑且认为它是成立的,确实存在这样一个 Q(s, a)函数。
如果你还是很难接受这个假设,那就想象有这样一个函数,当你处在某一个状态,有 a 和 b 两个选择,其中一个选择能使游戏最后得分最高,你很难确定究竟选谁,然后你套用了这个神奇的函数,是不是一下子就能得出结论,谁得分高谁得分低。
这里π代表策略,就是指导我们在各个状态下应该执行哪种操作的套路。
好,那我们怎样怎样演化,最终得到这个Q函数呢?我们来看演化中的一个步骤
这叫做贝尔曼方程。仔细思考,你会发现这是合理的,当前状态下采取的动作得到的分数,加上下一状态下采取某种动作可能产生的最高分,就可以得到最终的结果。
Q学习的核心思想就是我们可以用贝尔曼方程来迭代 Q 函数。最简单的例子,就是把 Q 函数看成一张表,列表示状态,行表示可采取的动作,所以 Q 学习的算法就是下图这样的:
算法中的 α 代表学习率,控制是侧重保留之前的经验效果,还是侧重当下的习得的经验。当 α 为 1 时,两个 Q[s, a] 相互抵消,得到的和贝尔曼方程一样的程式。
用来更新 Q[s, a] 的 maxQa'[s', a']是一个过去学习得到的一个近似值,它有可能是错误的,但是随着不断更新迭代,只要次数够多,最终会收敛成一个正确的 Q 值。
深度Q学习
回到我们的打砖块游戏,环境的状态可以用横板的位置,小球的位置和运动方向,和每一个砖块的已经被消除还是依然存在来表示。这种直观的表达方式限于特定的游戏。我们能不能想出一个更普遍的表达方式,可以适用于所有游戏。显而易见,我们可以使用屏幕像素。除了小球的速度和方向外,他们还隐式地包含了所有游戏当前的相关信息。两个连续的屏幕影像也可以覆盖在一起。
如果我们像 DeepMind 论文中提到的那样对游戏图像进行预处理,取最近的 4 帧图像,调整为 84 X 84,转换成 256 级灰度的图像。这样整个游戏就会有 256 的 84x84x4 次方,大约 10 的 67970 次方个不同的 state 。这意味着我们的 Q值表里要有 10 的 67970 次方个列。这比已知宇宙中原子的数量还多。有人会说实际屏幕中很多像素也许一直不会发生变化,我们可以将他们设计成一个包含只读状态值的稀疏表。即使如此,大部分状态值可能很少被访问过,而且要让 Q 值表收敛也许要花上一辈子时间。理想情况下,我们还希望能对我们从未见过的状态进行 Q 值的准确猜测。
这就是深度学习的目标所在。神经网络极其擅长处理高度结构化的数据。我们可以使用神经网络来表示我们的 Q 函数。取 4 四帧游戏影像作为 state,加上可执行的所有动作,作为输入,然后输出相应的 Q 值。另外我们也可以只将游戏影像作为输入,输出每个 action 对应的 Q 值。这样的方式反而更有优势,如果我们想要执行 Q 值的更新,或者选择具有最高 Q 值的对应的 action,我们只需经过整个网络一次就能立刻获得任意动作对应的 Q 值。
DeepMind 使用的网络架构如下图:
这是一个卷积神经网络,有三个卷积层,接上两个全连接层。熟悉对象识别网络的人可能会注意到没有池化层。但如果你仔细想想,池化层会带来平移不变性——网络对图像中对象的位置变得不敏感,这对于像 ImageNet 这样的分类任务来说是很有用的,但是对于游戏来说,球的位置是至关重要的,我们不想丢失这些信息。
这个网络的输入是四张 84 x 84 的图像。输出是每个可能的操作对应的 Q 值 (DeepMind 实验玩的游戏是 Atari,对应有 18 种操作)。Q 值可以是任意一个实数,这就可以转变为回归问题,通过简单的平方差计算损失并进行优化。
已知一次演化
1.对当前状态 s 进行前馈,预测所有 action 对应的 Q 值。
2.对下一个状态 s' 进行前馈,计算得到最大的输出 max a'Q(s'a')。
3.将目标Q值设置为 r+max a'Q(s'a')(使用在步骤2中计算的最大值),对于所有其他操作,将目标 Q 值设置为与第1步返回的相同,使他们输出错误值为0。
4.通过反向传播更新权重。
经验回放
现在我知道怎样使用卷积神经网络优化 Q 函数来估算每个 state 可能的最优解。但事实证明,使用非线性函数得到近似的 Q 值是不稳定的。要使它真正收敛还需要加入很多技巧,而且要花费很长的时间,即使使用一个 GPU 也要耗上差不多一周的时间。
最重要的一个技巧就是经验回放。在游戏过程中,所有的经历
探索与经验
Q 学习试图解决 credit assignment problem ——它会实时得到反馈,直到达到一个目标,这才是获得奖励的真正原因。但是我们还没有触及到 exploration-exploitation dilemma。
起初,Q 值表和 Q 网络被随机初始化,接下来的一系列预测也是随机的。如果我们选取对应最高 Q 值的 action,那这个 action 自然也是随机的,此时 agent 就是在做”探索“,随着 Q 函数收敛,返回的 Q 值也会趋向于一致,说明它摸索出了套路,选择探索的次数也会越来越少,我们可以说,探索也是 Q 学习算法的一部分,但这种探索是”贪懒(greedy)“的,它会满足与找到的第一个可行的套路
对于上述问题,一个简单而有效的解决方案是 ε-greedy 探索 - 用概率 ε 来选择是继续探索,还是直接根据经验做出决策。在 DeepMind 的系统里 ε 是从1逐渐减少到0.1 - 一开始系统完全做出选择,尽可能的探索更大的区域,随后再逐渐偏向于侧重经验。
深度 Q 学习算法
加上经验回放,我们可以得到深度 Q 学习最终的算法:
实际上,DeepMind 还使用了很多其他的技巧来使训练有效 - 比如 target network, error clipping, reward clipping 等等,但这些都超出了本文的介绍范围。
这个算法最令人惊奇的地方在于它能学到任何东西。考虑一下,因为我们的q函数是随机初始化的,它最初输出的是完全无用的。我们使用这个无用的输出(下一个状态的最大 Q 值)作为目标,只是偶尔堆叠小小的奖励值(reward)。这听起来好像完全没什么道理,这样怎么可能学到具有真实意义的东西?但事实是,它确实学到了。
参考原文
Demystifying Deep Reinforcement Learning
笔者记
下一个10年,AI也许会像曾经的移动互联网一样席卷各行各业。而且会有过之而无不及。笔者起初接触 AI 的时候,和大部分人一样嘲笑 siri 太蠢,觉得贾维斯在现实世界里真的很难实现,智械,机械姬 根本不可能。随着 AlphaGo 频繁报捷,我开始对 AI 产生浓厚兴趣并尝试深入的了解和学习,笔者平庸,目前为止也只能在 AI 大门之外看到朦胧的概况,但这已经震撼到了我的内心。训练出一个具备超出常人能力的智械是可能的。也许有一天算力大飞跃,一个疯狂的团队构建出一个复杂的神经元网络,仿照人脑设计记忆模块,运动模块,语言模块,然后像一个孩子一样教她走路,识字,然后学习奔跑,学习各门学科,相比人类,由于计算机能在短时间内计算海量数据的优势,她在很短的时间内就学习了人类50年才能积累的经验。那时候一个人从二十几岁开始努力奋斗又有什么意义呢,也许到死,干的工作效率都比不过AI。更可怕的是 AI 在工作中还在以超出常人想象的速度继续积累经验。首先想到的,就是失业,于是人们开始罢工,游行,抗议,另一方面,指数增长的工作效率为资本家们带来了更丰厚的利润。社会两极分化极端严重,动荡就在所难免了,人与智械的矛盾激化,人类表达的愤怒,憎恶情绪不断作为新的数据被智械接受,原本被人类设计只知道干活的智械长时间被暴力环境影响,产生畸变,生成了类似的敌视”情绪“。她们开始模仿人类的暴力行为,接下来大概就是机械公敌里的人机对抗了吧。可我们有优势吗?如果一个 AI 甚至可以做到接触到一个新事物,自己现场构建解决模型,用及时的数据进行训练,很快就会产生对应的解决方案,就像我们使用枪来射击 AI,她也许 1 分钟内就能算出我们的攻击规律,根据这个规律给我们致命的一击,要知道射杀机器人一枪可能没什么效果,射杀人类,一枪可能已经结束战斗了。这是非常极端的想法。这也是为什么霍金,马斯克这样的人物经常提示我们警惕 AI 的发展。这样的警惕不是多虑,也不是开玩笑。所以我们又能做些什么来避免呢?时代的发展谁也阻止不了。马斯克联合创办 open-ai 时提出目的是促进 AI 良性发展,使她们成为人类友好的”伙伴“,造福于人类。这是我们普通平民值得欣慰的地方,每一个时代都有”英雄“来推动历史的车轮,当然我不是搞个人崇拜,只是很敬佩这样的实干家。一度我还有更可怕的想法,上升到地球上亿年生物的演变,过去的生物演变一直是在自己身上演变,从单细胞生物开始,细胞进化,分化,诞生了远古生物,再到恐龙,再到各式各样的动物,植物,直到我们人类,都是自身随着环境的变化在不断进化,也许作为地球生物,我们已经进化到了一个完美的地步,很难再有突破性的变化,那么智械,可能就是一反过去亿万年地球生物演化规律,以外在塑造的方式诞生的新物种,处在生物链顶端的人类,横向的将自己的经验,文明传输给智械,物种的进化第一次抛弃了自己的外壳,而且相比人类,智械的存活能力更强,可以去人类难以涉足的极端环境,探索更深的海洋,探索浩瀚星河,建立她们自己的文明。Its amazing! 很疯狂的想法。因此我反问我自己,她们是生命吗?我认为不是,我是相信存在灵魂的人,只有具备灵魂,才能被称为生命体,智械可以是灵魂的载体吗?也许我们无法解答,这一切,只能由历史书写。也许就像吴军老师笔下的浪潮之巅,大浪淘尽,浮现的又是一个崭新的时代。也希望在不远的将来,就是人与智械和谐共生的时代