2019 iOS面试题大全---全方面剖析面试
2018 iOS面试题---算法相关
1、七种常见的数组排序算法整理(C语言版本)
2、2019 算法面试相关(leetcode)--数组和链表
3、2019 算法面试相关(leetcode)--字符串
4、2019 算法面试相关(leetcode)--栈和队列
5、2019 算法面试相关(leetcode)--优先队列
6、2019 算法面试相关(leetcode)--哈希表
7、2019 算法面试相关(leetcode)--树、二叉树、二叉搜索树
8、2019 算法面试相关(leetcode)--递归与分治
9、2019 算法面试相关(leetcode)--贪心算法
10、2019 算法面试相关(leetcode)--动态规划(Dynamic Programming)
11、2019 算法面试相关(leetcode)--动态规划之背包问题
翻转二叉树
二叉树的前序遍历
二叉树的中序遍历
二叉树的后序遍历
验证二叉搜索树
二叉树的最近公共祖先
二叉搜索树的最近公共祖先
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树
二叉树(Binary Tree)是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树,至少有2k-1个叶子节点,至多有2k-1个节点。
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
从二叉树的定义来看,算是比较适用递归算法的数据结构了
iOS:分别用OC和swift实现二叉树,并绘制到屏幕上
二叉树
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
一、 翻转二叉树
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
备注:
这个问题是受到 Max Howell 的 原问题 启发的 :
谷歌:我们90%的工程师使用您编写的软件(Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了。
又是经典的翻转。
直接用递归解法,分别递归地交换左右子树
var invertTree = function(root) {
if(!root) return root
let right = root.right
root.right = invertTree(root.left)
root.left = invertTree(right)
return root
};
二、 二叉树的前序遍历
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,2,3]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。
简单说其遍历顺序就是:根--左--右
使用递归可以很容易实现。
var preorderTraversal = function(root) {
return helper(root,[])
};
var helper = function(root,nums){
if(!root) return nums
nums.push(root.val)
helper(root.left,nums)
helper(root.right,nums)
return nums
}
不过题目有要求用迭代算法,这里我们可以想到之前提过的数据结构:栈
我们可以先将父结点的值放到数组里,然后将父节点入栈,等遍历完左子树,再出栈,去遍历右子树。
var preorderTraversal = function(root){
let treeStack = []
let res = []
while(root || treeStack.length){
while(root){
res.push(root.val)
treeStack.push(root)
root = root.left
}
if(treeStack.length){
root = treeStack.pop()
root = root.right
}
}
return res
}
三、 二叉树的中序遍历
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。若二叉树为空则结束返回,否则:
(1)中序遍历左子树
(2)访问根结点
(3)中序遍历右子树
简单说其遍历顺序就是:左--根--右
同理,用递归也可以很简单的实现。
var inorderTraversal = function(root) {
return helper(root,[])
};
var helper = function(root,nums){
if(!root) return nums
helper(root.left,nums)
nums.push(root.val)
helper(root.right,nums)
return nums
}
如果不用递归,用迭代呢?一样,也可以用栈去实现,先把父结点入栈,去遍历左子树,然后出栈将父节点放进数组,在同样去遍历右子树
var inorderTraversal = function(root){
let treeStack = []
let res = []
while(root || treeStack.length){
while(root){
treeStack.push(root)
root = root.left
}
if(treeStack.length){
root = treeStack.pop()
res.push(root.val)
root = root.right
}
}
return res
}
四、二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。即:
若二叉树为空则结束返回,否则:
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根结点
简单说其遍历顺序就是:左--右--根
和前序中序一样,用递归也可以很简单的实现。
var postorderTraversal = function(root) {
return helper(root,[])
};
var helper = function(root,nums){
if(!root) return nums
helper(root.left,nums)
helper(root.right,nums)
nums.push(root.val)
return nums
}
那如果不用递归用迭代呢?
leetcode上的前序中序遍历两道题都是标注的中等难度,而这道题却是标注成困难难度。
因为如果还是用之前的思路即还是用栈,是没办法直接实现的。
我们可以以根-右-左顺序入栈,然后一直向左遍历,直至左右子树都为空。出栈并保存到数组中,然后一直重复以上,这里需要注意的是,由于父结点已经遍历过了,这里一直出栈会造成死循环。所以我们还需要引入一个参数pre,来记录上次遍历的树,如果是栈尾的左右子树,则说明该结点已经遍历过,不再重复遍历。
var postorderTraversal = function(root) {
if(!root) return []
let treeStack = [root]
let res = []
let pre
while(treeStack.length){
root = treeStack[treeStack.length - 1]
if((!root.left && !root.right) || (pre &&(pre == root.left || pre == root.right))){
res.push(root.val)
treeStack.pop()
pre = root
}else{
if(root.right) treeStack.push(root.right)
if(root.left) treeStack.push(root.left)
}
}
return res
}
五、 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
示例 2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
验证二叉搜索树,其实就是验证其是否有序,我们可以对其进行中序遍历,如果遍历后的数据是有序的,则说明是二叉搜索树,反之则不是。
var isValidBST = function(root) {
if(!root) return true
let nums = []
helper(root,nums)
for(let i = 0; i < nums.length - 1; i++){
if(nums[i] >= nums[i + 1]) return false
}
return true
}
var helper = function(root,nums){
if(!root) return
helper(root.left,nums)
nums.push(root.val)
helper(root.right,nums)
}
那么能不能用o(1)的空间复杂度来解决呢?事实上我们没必要把数据都保存下来,对于右子树而言,只要所有右子树都大于其父节点即可,同理,所有左子树小于其父节点即可。
我们可以用两个变量:min和max,对于左子树,则判断是否小于min;对于右子树,则判断是否大于max
然后不断递归遍历,同时更新min和max
var isValidBST = function(root) {
return helper(root,undefined,undefined)
}
var helper = function(root,min,max){
if(!root ) return true
if(min != undefined && root.val <= min) return false
if(max != undefined && root.val >= max) return false
return helper(root.right,root.val,max) && helper(root.left,min,root.val)
}
六、 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
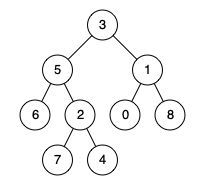
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
首先可以确定如果root为null或者p或q是根节点,那么说明最近的公共祖先就是根结点root。
我们同样可以使用递归去实现,分别递归左右结点,将其设为根节点,如果返回null,说明公共祖先在另一侧,如果都为null,说明公共结点就是root
var lowestCommonAncestor = function(root, p, q) {
if(root == null || root == p || root == q) return root
let left = lowestCommonAncestor(root.left,p,q)
let right = lowestCommonAncestor(root.right,p,q)
return !left ? right : (!right ? left : root)
}
或者我们可以同时分别求p和q的最近祖先
var findLowestAncestor = function(root,p){
if(root == null || root == p || root.left == p || root.right == p) return root
return findLowestAncestor(root.left,p) || findLowestAncestor(root.right,p)
}
一层一层往上遍历,直到p和q的祖先相遇
var lowestCommonAncestor = function(root, p, q) {
let qSet = new Set()
qSet.add(q)
while(p != q){
if(qSet.has(p)) return p
while(q != root){
q = findAncestor(root,q)
if(p == q) return p
qSet.add(q)
}
p = findAncestor(root,p)
}
return p
};
七、 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
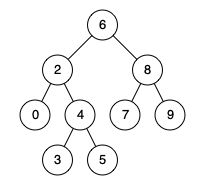
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
题目中的p和q有可能两个都在同侧,在递归的过程中,另一侧则没有必要去递归了,但因为二叉树无序,所以上边的算法没办法去判断,就算p和q不在另一侧,也只能继续递归下去。
而在二叉搜索树中,上边的那个算法就可以优化下
如果p和q都小于root的值,则说明p和q都在左侧,向左边递归即可;
如果p和q都大于root的值,则说明p和q都在右侧,向右边递归即可;
否则,就说明p和q在root的左右两侧,则其最近公共祖先就是root。
如果(root.val - p.val) 和 (root.val - q.val)的积是正的,则说明他们在同一侧
var lowestCommonAncestor = function(root, p, q) {
return (root.val - p.val) * (root.val - q.val) <= 0 ? root : lowestCommonAncestor(root.val >= q.val ? root.left : root.right, p, q)
};
这里当然也可以不用递归
var lowestCommonAncestor = function(root, p, q) {
while ((root.val - p.val) * (root.val - q.val) > 0) root = p.val < root.val ? root.left : root.right
return root
};