不倒嗡嗡
2016年10月10日,在圣地亚哥召开的美国计算力学等几何分析会议上,受等几何分析的创始人Tom Hughes博士的邀请,老顾做了题为“基于曲面叶状结构理论的六面体网”的报告,汇报了和大连理工大学罗钟铉、雷娜教授团队合作的关于神圣网格研究成果【1】。这一报告引起了与会者的广泛兴趣,许多人认为这是神圣网格问题理论研究的一个突破。Tom Hughes博士表示这是一项非常重要的工作;T-Spline之父,CAD领域的泰斗Tom Sederberg教授表示祝贺;犹他大学CAD领域的著名学者Elaine Cohen教授表示这是一个重要突破;佛罗里达大学,CAD领域的著名学者Jorg Peters教授给予了高度评价。Jorg教授认为这项工作从原则上解决了神圣网格问题,理清了体样条的奇异点和奇异曲线的性状,为构造全局光滑的体样条清除了障碍。他认为这方面学术上的研究已经成熟,剩下的工作应该被工业界接手来进一步完善。也有一些欧洲的学者纷纷索要论文,以进行跟踪复制。德国维尔斯特拉斯应用分析和随机(Stochastic)研究所的斯杭博士,不远万里来纽约访问。充分的讨论之后,他对神圣网格问题的彻底解决充满了信心。
历史回顾
2016年3月22-24日,老顾专程拜访了犹他州的杨百翰大学(Brigham Young University)的Tom Sederberg教授。Sederberg教授为大连理工大学的学者签名赠书。
2007年,SIGGRAPH 终身成就奖得主Tom Sederberg教授将老顾介绍给计算力学领域的泰斗Tom Hughes教授。那时,Hughes教授刚刚发起等几何分析(Isogeometric Analysis)的革命,和传统有限元方法比较,等几何分析可以提高计算精度,简化设计和分析流程。但是,等几何分析需要一个前提条件:将样条曲面转换成体样条表示。而这一点,需要计算结构化神圣网格(Structured HolyGrid)。Sederberg、Hughes和老顾在华盛顿聚会,就结构化神圣网格问题进行了深入地讨论。
美国三院院士(国家工程院,国家科学院,国家科学与艺术院), Tom Hughes博士,发起了等几何分析的革命。
近十年来,老顾拜会了国内、国际许多著名专家学者,对这一问题的认识逐步加深。在盐湖城、在合肥,中国科技大学的陈发来教授多次告诉老顾:“这一领域的绝大多数研究都是比较经验性的,缺乏理论支撑。需要发现和建立严谨、普适的理论框架。”
法国Inria的Pierre Alliez教授,德国柏林自由大学的Konrad Polthier教授都是网格生成领域的专家,他们都有自己独到的见解。Aliez教授建议网格的边应该和曲面的主曲率线尽量吻合,Polthier教授建议用分支覆盖(Branch Cover)将标架场转换成微分形式。在巴黎,老顾和法国Inria的Bruno Levy教授交流过基于Centroidal Voronoi Tessellation的体网格生成算法。在里昂,老顾和几何逼近论大师Jean-Marie Movan教授探讨过网格质量和曲率收敛的关系。在科大刘利刚教授举办的图形学暑期班上,浙江大学的黄劲教授和老顾探讨了这个问题。黄教授在这个领域耕耘多年,具有宝贵的第一手经验,他对于用标架场生成六面体网的算法中奇异点、奇异线的分布问题深感兴趣,由于缺乏理论根基,奇异线的产生和分布不可控,其性状的分析也非常困难。在路易斯安那的巴吞鲁日,李新教授告诉老顾用空间形变来生成体网格所遇到的退化情形。在波士顿的哈佛校园,赵辉博士和老顾探讨过四边形网格成为polycube边界的拓扑条件。在香港,雷诺铭教授和老顾讨论过如何用拟共形几何手段来提高网格质量。在数字几何,计算力学,计算机辅助设计等诸多领域,几乎所有的学者都对相关问题充满浓厚兴趣。
大连是中国船舶设计、船舶制造的工业基地之一,精密机械加工方面工业基础深厚。大连理工大学历经半个多世纪的学术积累,具有非常雄厚的CAD/CAE科研基础。王仁宏教授开创的学派,一直在国内计算数学、计算几何领域占据领袖地位;计算力学的泰斗钱令希院士开创的计算力学专业,一直在国际上领先。王仁宏教授的弟子,大连理工大学的校长助理罗钟铉教授邀请老顾前去访问讲学,对于神圣网格问题的研究给予了高度重视和大力支持。在大连理工讲学期间,老顾和计算力学方向的关振群教授交流了科研心得。关教授在网格生成领域有数十年的研究经验,他认为对偶网格能否分解为不自相交的封闭曲线具有重要意义。关教授和香港大学的王文平教授有过深入交流,王教授指出网格的光滑性和调和能量密切相关。大连理工大学的雷娜教授为了解决神圣网格问题在纽约访问了一年的时间,在这一年中,大家日以继夜,高度专注于这一问题,终于在理论上取得了长足进展。
等几何分析
在计算机辅助设计(Computer Aided Design CAD)领域,设计的机械都是由所谓的样条曲面(Spline Surface)来表示,特别是经典的NURBS曲面(Non-Uniform-Rational-B-Spline)。但是在计算机辅助工程(Computer Aided Engineering CAE)领域,机械的力学热学性能的数值模拟却是用有限元方法(Finite Element Method FEM)来处理。在通常情形下,有限元方法将机械实体进行三角剖分,如图2和图3所示,然后用分片线性函数来逼近光滑解。
CAD和CAE的基本数据结构的差异带来了工程上的巨大困难。首先,将CAD的NURBS样条表示转换成有限元的剖分,即所谓的网格生成,这需要困难而复杂的计算和操作。在波音航空公司中,网格生成这一步骤占据整个流程70%以上的时间和成本,真正求解偏微分方程只占30%不到的成本。其次,数学上的处理也比较间接而迂回。物理规律一般表示成高阶偏微分方程,而有限元方法一般用一阶光滑的分片线性函数。为了处理光滑阶数不够的矛盾,有限元方法一般采用偏微分方程的变分形式求得弱解。比如,热力平衡态的温度分布满足拉普拉斯方程,这是一个二阶椭圆型偏微分方程,未知函数需要具有二阶光滑性;用有限元的伽辽金法求解时,我们将拉普拉斯方程转换成优化调和能量的问题,而调和能量只需要一阶光滑性。
Tom Hughes博士深刻地洞察到了CAD和CAE基本数据结构不一致性这一基本问题,提出了等几何分析(Isogeometric Analysis)这一颠覆的理论框架,引发了CAD/CAE领域的一场革命。等几何分析的根本思想就是统一几何设计和几何分析的数据结构,工业设计和工业仿真都用样条表示。这样做的好处是显而易见的。
首先,等几何分析方法具有理论处理的便捷性。在等几何分析的框架下,未知函数被表示成NURBS基函数的线性组合。线性组合系数是待定的未知变量。因为NURBS基函数具有高阶可微,被高阶微分算子作用后所得函数依然是可以被表示为NURBS函数。这样,我们可以用待定系数法来求解偏微分方程。例如,为了求解拉普拉斯方程,我们在定义域中选取一些采样点,然后利用未知函数在采样点处的拉普拉斯等于零来求解待定系数。这种方法被称为是colocation方法,它不需要将偏微分方程转换成变分能量,因此数学手法上更为简洁直接。今年(2016年),在等几何分析领域的学者们在理论上首次证明了通过精心挑选采样点的位置,colocation方法求得解的精度达到伽辽金法求得解的精度。这在理论上将等几何分析方法提到了和有限元法平起平坐的地位。
其次,等几何分析方法省却了从样条到网格的转换过程。但是,这里隐藏着极大的挑战。传统的CAD模型只是将机械零件的表面用样条来表示,而等几何分析需要的是机械零件实体的样条表示。从样条曲面转换到体样条表示,这是等几何分析的根基。而这一根本问题的解决依赖于六面体网格的生成,即神圣网格问题的妥善解决。同时,更进一步,经典的神圣网格不要求结构化的网格,而等几何分析要求的是结构化六面体网格。所谓结构化,就是指局部上,六面体网格具有直积结构,和标准欧式空间中整数格点构成的网格同构。因此等几何分析提出的神圣网格问题更具有挑战性。
三位一体
等几何分析提出的基本理论问题可以大致归纳如下:给定空间中封闭的高亏格曲面,剖分其内部体积,
结构化的六面体网格(神圣网格)是否存在?
如果存在,最少奇异点的个数是多少?
如果存在,最少奇异曲线的条数是多少?
这种神圣网格是唯一的吗?所有的神圣网格的集合如何描述?
如何构造这种神圣网格?是否存在自动算法?
在过去的二十年间,Thurston、Mitchell、Erickson利用子流形浸入理论和同调群理论解答了非结构六面体网格的存在性问题,他们的方法对于结构性六面体网格的问题无能为力。最近,大连理工大学的罗钟铉、雷娜团队和老顾团队合作,利用曲面的叶状结构(foliation)理论和黎曼面的亚纯微分理论(Meromorphic Differential)理论对这些问题给出了确定的回答,从而将结构化神圣网格的理论向前推进了一步。
这一理论的核心在于证明了三个基本几何拓扑概念本质上是一致的,可着色四边形网格(红-蓝网格)、带测度的叶状结构(measured foliations)和全纯二次微分(holomorphic quadratic differentials),即所谓的三位一体。对于上面提到的基本问题,我们给出的解答是:
结构化的六面体网格存在,并且无穷多。
对于边界曲面的亏格为g>1,一般情况下,奇异点有4g-4个。
最少内部奇异曲线的条数是2g-2条(边界上有4条)。
这种神圣网格不唯一,其中边界曲面上诱导的四边形网格构成一个线性空间,其维数是6g-6维。
存在构造方法,其算法流程可以完全自动化。
红蓝网格
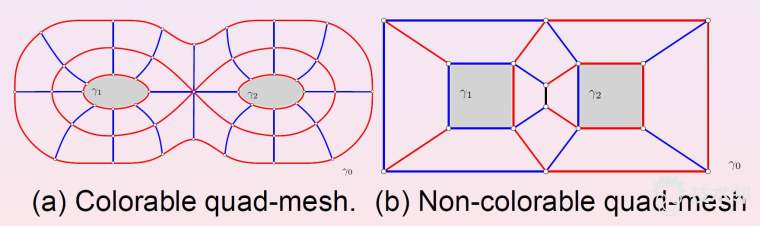
图4显示了所谓的可染色四边形网格(或者红-蓝四边形网格)(colorable quad-mesh)。假设给定曲面上的四边形网格,如果我们能够将所有的边红-蓝染色,使得每个四边形中,两组对边分别被染成红色和蓝色,则此四边形网格被称为是可染色的。
有些四边形网格是不可染色的,如图5右帧所示,我们无法确定中间黑色边的颜色,无论我们选择红色或是蓝色,都会产生矛盾。我们证明了如下的引理:
四边形网格可染色的充要条件是所有顶点都和偶数条边相邻。
假设输入曲面是封闭曲面,如图4中的兔子曲面,给定一个可染色四边形网格,如兔子身上的红-蓝网格,可染色四边形网格的所有红边组成有限条圈,每条圈没有自相交点。同样,所有蓝边也组成有限条圈,每条圈也没有自相交点。我们考察可染色四边形网格的对偶网格,则对偶网格由有限条圈组成,并且每条圈都没有自相交。
我们将兔子曲面进行细分(subdivision),每个四边形被劈成四个子四边形,则红圈和蓝圈的条数加倍。我们不停地细分下去,则兔子曲面被红圈覆盖,同时也被蓝圈覆盖。换言之,兔子曲面被分解成红圈的并集,也被分解为蓝圈的并集。局部上看,红(蓝)圈层层堆叠,彼此没有交叉或者折叠,由此,我们得到了两个叶状结构(foliation)。
叶状结构
所谓叶状结构(foliation),就是将n维流形分解成(n-1)维子流形,其分解方式局部上具有直接结构,如图6所示,我们将亏格为3的曲面分解成一族曲线,每条曲线被称之为叶子。每片叶子可以是封闭曲线,或者无限延长的螺旋线。曲面上三条叶子交汇的点被称为是奇异点,一般情况下亏格为g>1的曲面上有4g-4个奇异点。在任意一个常点处(非奇异点),存在一个领域,叶状结构具有直积结构。
我们可以定义一个测度,这个测度的几何意义如下:任给一条曲线,此曲线横截通过了叶子的条数等于这条曲线的测度。
叶状结构的叶子实际上是曲面上的光滑流线,其速度切向量场为流场。最为光滑的流场被称为是所谓的调和场,其旋量处处为零,同时散度也处处为零。由此,曲面的叶状结构和曲面上的全纯微分开始联系起来。
全纯微分
图7解释了曲面上全纯微分的概念。给定一个亏格为一的小猫曲面(左帧),我们可以周期性地将曲面保角地映射到平面上面(中帧)。或者更为严密地,我们将小猫曲面上的黎曼度量,经过投影映射拉回到小猫曲面的万有覆盖空间上面,存在从万有覆盖空间到整个欧式平面的共形映射。这个共形映射的导数就是定义带小猫曲面上的一个全纯1-微分形式。这个共形映射将平面上的水平线拉回到曲面上,形成全纯微分的水平轨道(即为右帧中的红色曲线),这个映射经平面上的铅直线拉回到曲面上的全纯微分的铅直轨道(即为右帧中的蓝色曲线)。给定一个全纯1-微分形式,则其所有的水平轨道形成曲面的一个叶状结构。
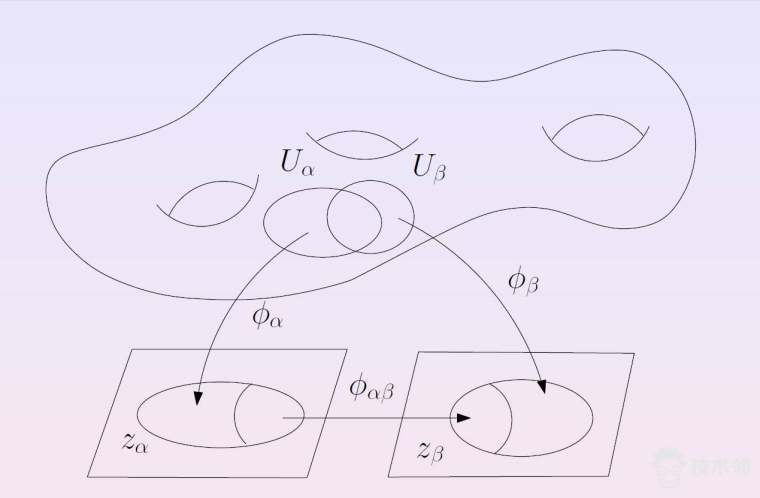
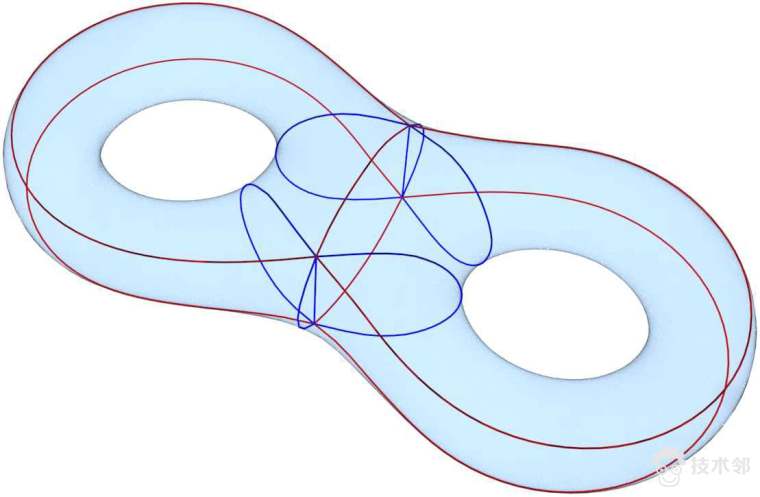
图8显示了亏格为二的曲面上的全纯二次微分,及其水平和铅直轨道。全纯二次微分的严格数学描述比较抽象费解,它是借助于黎曼面的结构来诠释的。如图9所示,作为流形的曲面,我们无法用一个坐标系来覆盖,只能用多个坐标系来覆盖。如果我们都采用复坐标,并且坐标变换都是可逆全纯函数,则曲面被称为是黎曼面。给定一个全纯二次微分(Holomorphic Quadratic Differential),则它在每个局部坐标系下都是某个全纯函数导数的平方。
曲面上所有的全纯二次微分构成一个线性空间,例如图10所示,前两个全纯二次微分之和等于第三个全纯二次微分。根据黎曼-罗赫定理,所有全纯二次微分构成的空间的维数等于6g-6。
经典的 Hubbard-Masure 理论【2】证明了可测叶状结构和全纯二次微分之间的等价关系,任给一个可测叶状结构,则存在一个全纯二次微分,微分的水平轨道诱导的叶状结构和给定叶状结构在一定意义下彼此等价。
由此,我们证明了可染色四边形网格、可测叶状结构和全纯微分之间的等价关系,即三位一体。
六面体网格生成算法
基于三位一体的理论,我们可以设计六面体网格的自动生成算法。下面我们用一个简单的例子来解释我们算法的主要流程。
首先,我们计算全纯二次微分群的基底;然后,通过线性组合求得一个全纯微分;全纯微分的水平轨道给出了曲面的一个叶状结构,如图11所示。
。
过奇异点的轨道被称为是奇异轨道,每条奇异轨道连接着两个奇异点,如图12所示。
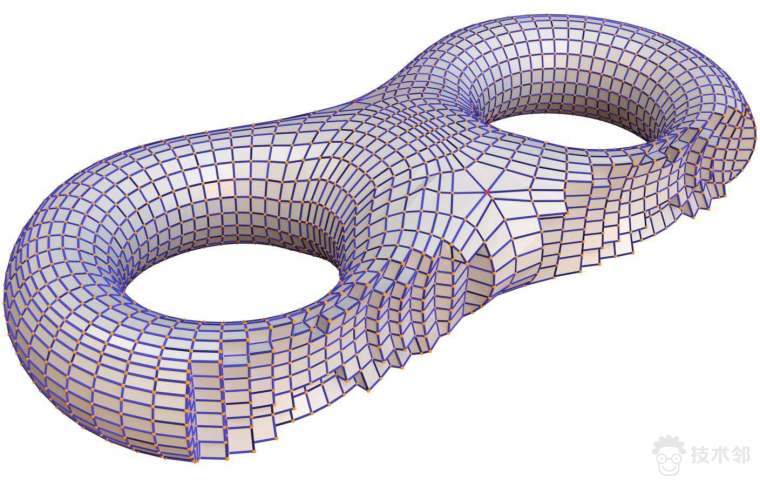
曲面的叶状结构诱导了曲面上的四边形网格(图13),奇异轨道将曲面分解成圆筒曲面(图14)。
每个圆筒曲面包含着一个圆柱体,表面的四边形网格向体内拓展成圆柱体的六面体网格,如图15所示。三个圆柱体交于一条奇异线。
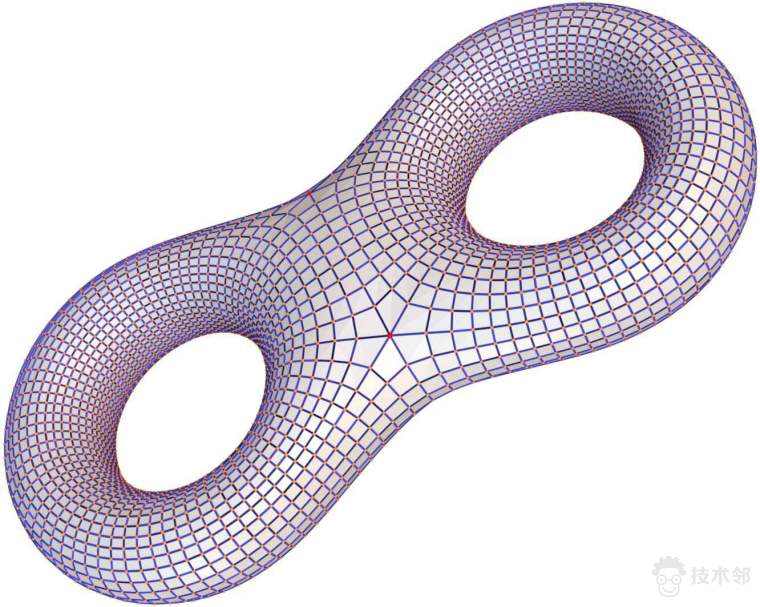
最后生成的六面体网格如图16所示,只有4个奇异点,两条内部奇异曲线,整体具有很好地结构性。
展望
目前,基于叶状结构的六面体网格生成算法侧重考虑了流形的拓扑结构和共形结构,而忽略了几何信息。在实际应用中,网格化需要充分考虑曲面的几何特征,特别是曲面的主曲率方向,曲面的特征曲线,尖锐的折角曲线等等。很多时候,我们需要加入更多的奇异点或奇异线,来使得网格化更好地适应几何特征。这些都是下一步需要发展的方向。
斯杭博士通过多年的实践经验,充分认识到从拓扑剖分到组合、几何剖分之间的巨大障碍。如何建立组合、几何剖分的障碍理论,在网格生成领域中具有根本的重要性。
虽然,等几何分析在学术界的研究日益蓬勃壮大,在工业界只有几家公司开始采用这一新兴技术。Tom Hughes在展望未来的时候,说出了非常具有哲理的一番话。他说历史上任何一个伟大的创造,都历经了三个阶段:
人们认为这种方法是不可能实现的,
人们认为虽然这种方法可以被实现出来,但是和现行的方法比较没有任何优势,因此没有必要采用这种方法,
人们须臾离不开这种方法。
他认为等几何分析目前正在前两个阶段,并且豪情满怀地畅想未来等几何分析必将取代有限元而成为业界主流。我们也倾向于认为,目前基于叶状结构的六面体网格生成方法介于第一和第二个阶段,我们有理由相信这种方法在不远的将来将大行其道!