串匹配算法也称作模式匹配算法,就是在目标字符串中查找子字符串,常用于文本搜索、入侵检测等领域,将目标字符串定义为T(t0,t1,... tn-1),将模式字符串定义为P(p0,p1...pm-1)。下面将来逐步讲解算法之美中的KMP算法。
1.BF算法
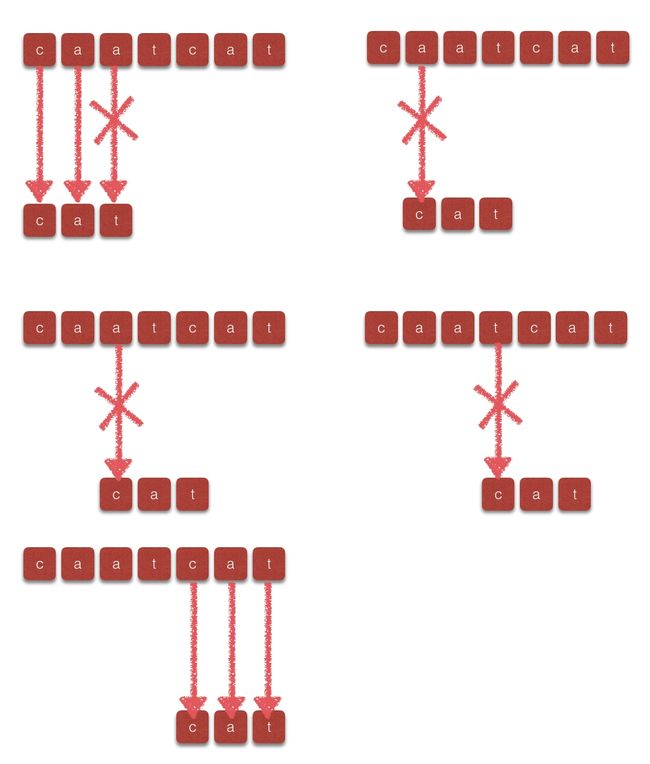
最简单的做法就是遍历目标字符串中的每一个字符与模式字符串中的字符进行逐一比较,不相同的时候保持目标字符串的索引不变模式字符串的索引加1,在进行逐个字符的比较,这种方式也称作BF(Brute Force)算法,如下图所示:
由此可见,BF算法的时间复杂度为O((n-m)*m),该方法简单、直观,但是由于每遇到一次失配都要将目标字符串的索引回溯,显然效率很低。
2.MP算法
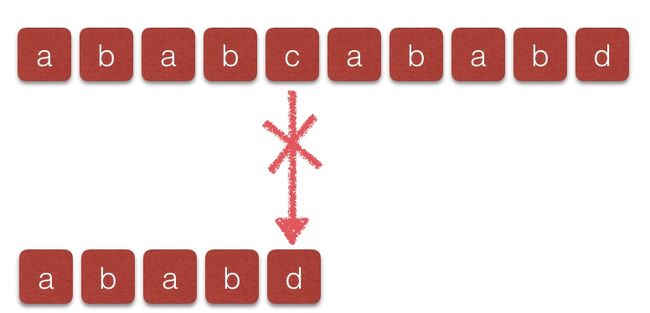
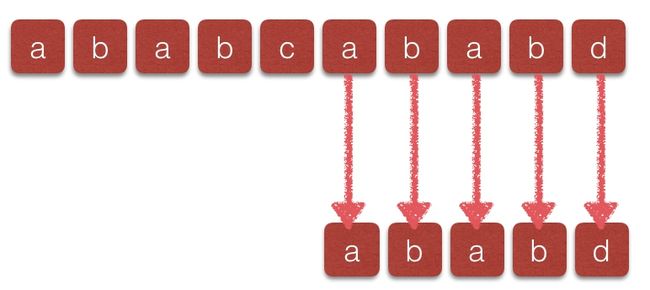
MP算法是由詹姆斯·莫里斯和沃恩·普莱特在1970年提出的一种快速匹配算法。该算法的主要特点是当失配情况发生时,目标字符串的索引不需要回溯,利用模式字符串的内部特征可以完全避免目标字符串的回溯,这样可以极大的提高检索效率。先举一个简单的例子对于目标字符串ababcababd与模式字符串ababd来说:
第一次失配发生在
t[i = 4] = c 和
p[j = 4] = d 处如果按照BF检索的话,下一次比较时字符串T和字符串P的起始位置分别为1和0,但是这样做完全没有必要,通过观察模式字符串可以发现,ababd中前四个字符具有相同的特征就是a[0]a[1] = a[2]a[3],那么下次匹配时,就不需要将目标字符串的索引回溯,我们只需要将模式字符串的索引位置变为j = 2就可以进行下轮的比较:
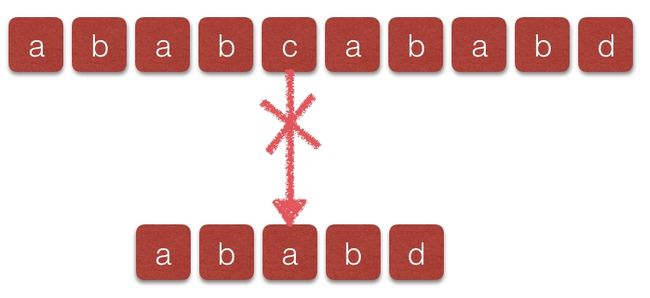
此时发现t[4] != p[2],需要比较t[4]与p[0]得到如下图:
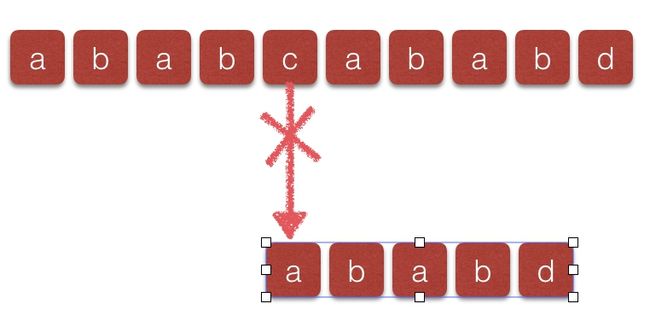
发现t[4] != p[0],然后将i加1,再与p进行比较:
逐个比较之后发现完全相等。
MP算法就是在对字符串进行匹配之前,先求出模式字符串中各个字符间的关系(由于模式字符串在进行匹配之前就可以确定),然后依据此关系与目标字符串进行匹配。记录模式字符串P中各个字符之间的关系的函数也叫作字符串的失效函数。让我们先来看看这个失效函数,先举一个简单的例子:目标字符串为aaaaab与模式字符串aaab的比较,当第一轮比较到i=3时,失配发生了,此时t[i] = a 与 p[i] = b不相等,由于模式字符串在i=3之前的字符都与目标字符串的字符相同即:t[0]t[1]t[2] = p[0]p[1]p[2],而且模式字符串中的前三个字符也完全相同即:p[0]=p[1]=p[2]那么下次比较的位置我们能准确的定位:目标字符串t[3]与模式字符串p[2]进行比较,因为t[1] = p[0] ;t[2] = p[1],所以如果从t[1]开始逐个与模式字符串中的字符比较就会造成浪费。失效函数是记录当失配发生时,模式字符串索引应该跳转的位置。
我们用f(i)记录当失配发生时,模式字符串应该回退的索引位置,则定义如下:对于长度为n的字符串,位于第m位的字符如果存在如下关系:p[0]...p[k] = p[m-k]...p[m],且满足该条件的k最大,那么f[m]=k,若不存在f(i) = 1,其中n > m , m > k。,当遇到失配发生时,我们只需要将模式字符串的指针移动到f(m-1) + 1处,而不需要移动目标字符串的指针。
可以简单的论证一下当存在匹配模式时(读者可以自行论证当不存在模式匹配时的情况):对于目标字符串T和模式字符串P(我们假设都从下标1开始),当T[i + 1 ... i + k - 1]的k-1个元素与P[1 ... k-1]相同,但是T[i+k] 与 P[k]比较时失配,如果f(k - 1) = j ,那么根据定义P[1...j] == P[k-j... k-1],也就是说T[i+k-j...i+k-1] = P[1...j],那么我们下次比较的就是T[i+k]与P[j+1]了,所以,当P[k]失配时,我们将下次比较的位置定位在P[f(k-1)+1],我们假设next[k] = f(k-1)+1,当失配在第k个字符串发生时,next[k]表示下次比较时,模式字符串的索引值。
下面的C代码就是求取模式字符串的next函数如下:
void MPPattern(const char * var , int *mpArr) {
size_t length = strlen(var);
int i = 0;
int j = mpArr[0] = -1;
while (i < length) {
while (j > -1 && var[i] != var[j]) { // 4
j = mpArr[j]; // 5
}
i++; // 1
j++; // 2
mpArr[i] = j; // 3
}
}
var 即为待求解的模式字符串,将最后求得的next[]存放在mpArr中,将j、mpArr[0]赋值为-1。首先看看简单的1、2、3这几个步骤,如果我们要求解的是aaaaa这样字符全部相同的模式字符串,自然而然,随着字符索引的增加,next[i]根据定义也应该是递增+1的,这三步很好理解。再来看看4、5步,如果向前遍历的过程中x[i]!=x[j],由于i总比j大,需要将j回溯,回溯的位置就是mpArr[j](其实就是f(k-1)+1),在进行比较,如果j = -1(mpArr[0])时,执行1、2、3步。
对于字符串aaabc执行的结果为
目标字符串与模式字符串比较代码如下:
int isTargetContain(const char* target , const char* pattern) {
size_t pLength = strlen(pattern);
int * a = calloc(pLength, sizeof(int));
MPPattern(pattern, a);
size_t tLength = strlen(target);
int i = 0 , j = 0;
while (j < tLength) {
while (i > -1 && target[j] != pattern[i]) {
i = a[i];
}
i++;
j++;
if (i >= pLength) {
int index = j - i;
i = a[i];
free(a);
return index;
}
}
free(a);
return -1;
}
其中i = a[i]依然表示的是回溯。
KMP算法
KMP算法与MP算法相似,唯一的不同点就是,f(m)不仅要满足p[0]...p[k-1] = p[m-k]...p[m-1],同时要满足条件P[k]!=P[m]。KMP是在MP算法上的优化,在与目标字符串比较时,T[i ... i + k - 1]的k-1个元素与P[0 ... k-1]相同,但是T[i+k] 与 P[k]比较时失配,按照MP算法的话,模式字符串应该回溯到f(k-1)+1这个位置,如果 P[f(k-1)+1]与P[k]相同的话,再次与目标字符串比较,肯定会失败。我们用kmpNext[]数组来记录KMP算法下失配时模式串的偏移:
- 如果kmpNext[j] = -1 表示P[j] = P[0],且P[j]前面k个字符与P开头的k个字符不等,或者相等但是P[j]!=P[k]
- 如果kmpNext[j] = k 表示模式字符串P中,字符P[j]前面k个字符与模式字符串开头k个字符相同,且 P[j]!=P[k]
- 其它情况kmpNext[j] = 0
kmp计算kmpNext[]的算法实现如下:
void KMPPattern(const char * var , int *kmpArr) {
int i ,j;
size_t length = strlen(var);
i = 0;
j = kmpArr[0] = -1;
while (i < length) {
while (j > -1 && var[i] != var[j]) {
j = kmpArr[j];
}
i++;
j++;
if (var[i] == var[j]) { // 1
kmpArr[i] = kmpArr[j];
} else {
kmpArr[i] = j;
}
}
}
其中回溯那部分代码与MP算法相同,唯一不同的是1处的代码,如果我们的模式字符串为aaaa,那么根据定义可知道,kmpNext[] = [-1,-1,-1,-1],这就是var[i]==var[j]这个判断做的事情,但是如果是字符串aaaab,那么kmpNext[] = [-1,-1,-1,-1,3],最后的3就是else里做的事情,复杂的模式字符串原理大致相同,可以自行论证。
kmp算法目标字符串与模式字符串比较的代码如下:
int KMP(const char *target , const char *pattern){
size_t targetSize = strlen(target);
size_t patternSize = strlen(pattern);
if (patternSize > targetSize) { return -1; }
int *t;
t = calloc(patternSize + 1, sizeof(int));
KMPPattern(pattern, t);
int i = 0 , j = 0;
while (j < targetSize) {
while (i > -1 && target[j] != pattern[i]) {
i = t[i];
}
i++;
j++;
if (i >= patternSize) {
free(t);
return (j - i);
}
}
free(t);
return -1;
}
结论
kmp算法由于先寻找模式字符串的内部特征来降低与目标字符串的匹配次数,时间复杂度为O(m + n),在进行匹配之前需要先将模式字符串的失效函数计算出来,在进行匹配时,如果匹配失败,不需要将目标字符串回溯,只需要将模式字符串的指针回溯值next[j]处从而提高效率。