Support Vector Machine
[学习、内化]——讲出来才是真的听懂了,分享在这里也给后面的小伙伴点帮助。
learn from:
https://www.youtube.com/watch?v=QSEPStBgwRQ&list=PLJV_el3uVTsPy9oCRY30oBPNLCo89yu49&index=29
台湾大学李宏毅教授,讲授课程很用心,能把我之前看过却不理解的知识很易懂、精彩的讲出来——respect
1、SVM
SVM是一个经典的二分类、监督学习算法。与logistic regression很像(需要先学此基础),主要独特之处有两点:
1.loss fuction 用 Hinge Loss。
2.模型 f(x) 使用了 kernel method。
下面依次理解这两个关键,来学习SVM。
2、Hinge Loss
2.1
SVM 算法结构与 logistic regression 或者 binary classification 基本一样:
![[机器学习] SVM——Hinge与Kernel_第1张图片](http://img.e-com-net.com/image/info8/ddb3be709bf341a5b526c3e8f4069e65.jpg)
在解决上面原L(f)不能做梯度下降时,与logistic regression使用 sigmoid + cross entropy不同,使用Hinge Loss,从而产生了Linear SVM。
logistic regression 与 Linear SVM两个算法唯一的不同之处就是使用了不同的loss function,前者使用的sigmoid+cross,而后者用 hinge 。
![[机器学习] SVM——Hinge与Kernel_第2张图片](http://img.e-com-net.com/image/info8/1f44b8b17608476eba9e2e48753e2f7c.jpg)
2.2
下面讲讲 loss function 那些事,理解这些后,将对 SVM 的 HInge 有很深的理解。
因为原本的loss fuction(下图中标①的loss function,下文简称L①)不能微分所以无法做梯度下降 ,所以我们要做的就是用一个可以微分的loss function(下文简称L②)来近似代替L①。我们知道L①的作用:当预测值与实际值相等时,L=0,不相等时,L=1(函数括号里成立时,函数值=0,否则为1,不清楚的可以查一下 kronecker 记号)。binary classification 中:
![[机器学习] SVM——Hinge与Kernel_第3张图片](http://img.e-com-net.com/image/info8/85a5518e44d64678994b8cac0256587a.jpg)
而y只等于+1或-1,所以预测正确时,即g(x)与y相等时,y一定与f(x)同号,预测错误时异号。(以0点为界,y·f(x)越大即就是预测正确,y·f(x)越小即为预测错误,下图中用yf(x)作图分析并说Larger value, smaller loss,应该是这样理解的)所以我们需要找这样一个L②来代替L①:当同号时,loss接近0;当异号时,loss很大。
下面是尝试使用不同的L②:
square loss: 不行。
连我们上面分析L②应有的性质都不满足,而已早在 logistic regression 里就知道了 square loss 是不适用这种离散型任务的。
![[机器学习] SVM——Hinge与Kernel_第4张图片](http://img.e-com-net.com/image/info8/c5a63b9433614c47b7aa24958164de91.jpg)
sigmoid+square
sigmoid+cross entropy
Hinge
Hinge 与 sigmiod+cross entropy 这两个loss function的区别:对于结果已经正确的样本数据,hinge 就不再继续产生loss用于继续提升,而sigmiod+cross entropy 会继续产生loss 使其再继续远离刚刚能正确分类的点(不满足于刚刚超过阈值)。
2.3
确定好了loss function之后,就可以做梯度下降了。
![[机器学习] SVM——Hinge与Kernel_第8张图片](http://img.e-com-net.com/image/info8/a42c4208fd4b47be8437bc3c17175e0e.jpg)
c(w)有很多都为0,不=0的那些c(w)即为 support vector.
SVM有很好的鲁棒性(robust),因为有很多数据(即那些c(w)=0的)不会影响结果,而 logistic regression 相比就没有这样的鲁棒性。
2.4 Linear SVM的另一种表示形式
3、kernel trick
下面是花书(Deep Learning)中关于SVM的部分,主要就是在说kernel,说的比较宏观比较笼统,先看一下有利于下面深入学习。
![[机器学习] SVM——Hinge与Kernel_第10张图片](http://img.e-com-net.com/image/info8/0a44875dc8de4da18d447d30b2f36965.jpg)
3.1
先概括一下我自己理解的kernel trick:利用很多机器学习算法的模型参数都能写成样本间内积的特点,利用核函数代替先转换空间(即非线性ϕ(x))再内积的方法,来学习非线性模型。
先知道一个事实:w是x的线性组合。
听起来可能难以相信:训练出的模型参数w是数据x的线性组合?解释一下:梯度下降更新参数w时,c(w)只能取0,±1,取0不用说了,取±1时,w就是在±学习率*x
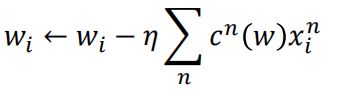
3.2 径向基函数
径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意一点c的距离,c点称为中心点,也就是Φ(x,c)=Φ(‖x-c‖)。任意一个满足Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数,标准的一般使用欧氏距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。在神经网络结构中,可以作为全连接层和ReLU层的主要函数。
![[机器学习] SVM——Hinge与Kernel_第14张图片](http://img.e-com-net.com/image/info8/6e3f4b269bb14bd897307930f6c037bd.jpg)
3.3 与神经网络
3.3.1 sigmiod kernel 与神经网络
用sigmiod kernel就相当于一个只有一层hidden layer的神经网络。
每个神经元的参数就是一个输入的data。神经元的个数 = support vector的个数。
3.3.1 SVM 与神经网络
其实kernel是可学习的,但是可学习性没有神经网络参数强,只能给几点kernel然后学习出他们的组合。
只有一个kernel相当于只有一层隐藏层,由多个Kernel组合相当于由多个隐藏层。

![[机器学习] SVM——Hinge与Kernel_第5张图片](http://img.e-com-net.com/image/info8/2e962ac3cad94539862ef7242690d8cb.jpg)
![[机器学习] SVM——Hinge与Kernel_第6张图片](http://img.e-com-net.com/image/info8/10be9fda7c2943d3b28d4e122de3d2f5.jpg)
![[机器学习] SVM——Hinge与Kernel_第7张图片](http://img.e-com-net.com/image/info8/a2b60f47addc4a32ad7f763590e867df.jpg)
![[机器学习] SVM——Hinge与Kernel_第9张图片](http://img.e-com-net.com/image/info8/b7b6265233d0419884028734318ae234.jpg)
![[机器学习] SVM——Hinge与Kernel_第11张图片](http://img.e-com-net.com/image/info8/179b5464cb164193b4f93a31693aab9d.jpg)
![[机器学习] SVM——Hinge与Kernel_第12张图片](http://img.e-com-net.com/image/info8/b9a36bfad48c47a1aba08028941215f7.jpg)
![[机器学习] SVM——Hinge与Kernel_第13张图片](http://img.e-com-net.com/image/info8/d9f915dc78c14ef88d1205b95ed0c335.jpg)
![[机器学习] SVM——Hinge与Kernel_第15张图片](http://img.e-com-net.com/image/info8/9befe5c6d18146358580a7899bd390ed.jpg)
![[机器学习] SVM——Hinge与Kernel_第16张图片](http://img.e-com-net.com/image/info8/01880ebddf9147b4969a3752727e8d47.jpg)