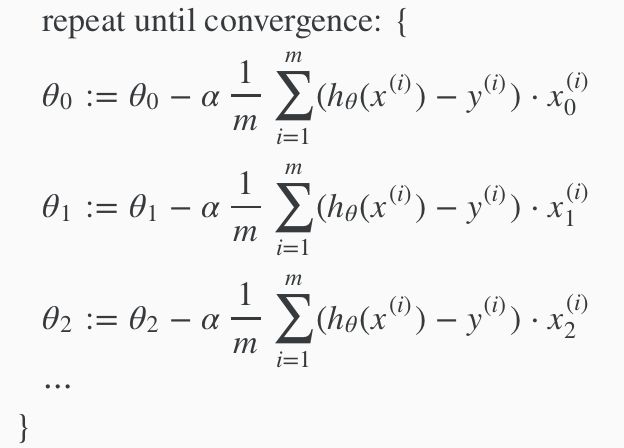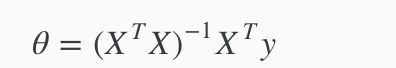要不要点紧呐
20天没发文章了,罪过罪过。
深夜了,就简单写一下今天了解到的一点关于Linear Regression的内容。
什么是Linear Regression,具体怎么Regression,什么θ0 + θ1x1 + θ2x2,什么梯度下降的,(包括下图中1/m∑(...)x是怎么来的)没什么意思,就不再赘述。
稍微需要注意的是下图中所示的 θ是如何在训练中被更新的,也就是梯度下降的具体公式。
看上去每一个 θ的更新方式都相同,只有细微的差别,具体是在求1/2m∑(...) 2这个式子对不同的 θ进行偏导时的不同,对哪个 θ求偏导,那个 θ的系数就会留下来,会微积分的同学们都应该明白。
而在实际情况中,训练集中的各种特征的特征值范围一般是不同的,例如预测房屋价格中,房屋面积的值的范围可能在1到1000,房屋年龄却仅仅是1到10,这样会造成什么样的情况呢,见下图。
绘图水平有限,但是意思到位了,在上述房价预测的例子中有两个特征,取值范围相差很远,可以想象,在θ与这2个特征运算的过程中,房屋面积所占的比重远远大于范围只有1到10的房屋年龄。换句话说,假设初始的θ为1左右,乘以1000的影响远远大于乘以10的影响。如上图,横纵坐标为两个特征对应的两个θ,图像为房价预测模型的cost function。图中红线表示出梯度下降进度,可想而知,这样情况下的梯度下降,进度很慢。因此这里引出一个叫做Feature Scaling的方法—— 特征缩放, 简单来说就是把输入减去所有输入的平均值 ,除以输入值的范围。从而将不同特征的不同输入值,全都框在一个差不多的范围之中。
例如上述1到10的房屋年龄,如果所有值的平均为7年,则将所有的房屋年龄减7,再除以房屋年龄的范围,1到10年,则为(10 - 1)。最后的结果是,(x - 7 )/ (10 - 1) 。
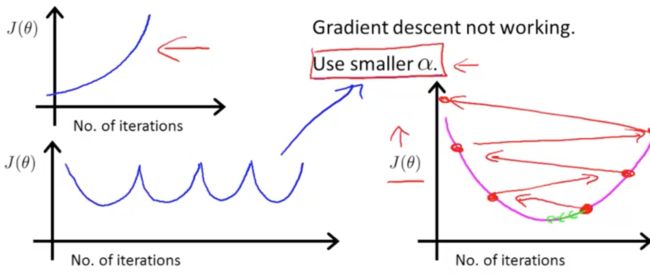
接下来,还是有关梯度下降,在正常情况下,cost function的值在每轮迭代都会下降。也就是说如果某一轮或某几轮或断断续续地总是上升,就说明训练一定是出了问题。
看下边图中左边的两个平面直角坐标系,都是cost function上升或升降夹杂的情况,再看右边的那个坐标系,从右下角的红点开始进行梯度下降,可是迈的步子太大,一步走了很远,不仅没有下降反而上升了,这样一步一步的,反而越训练cost function的值越大。所以怎么办呢,当然是把步子迈小一点。因此我们把learning rate改小。
而大家也知道,步子太小,走得就很慢,所以找一个合适的learning rate也是很必要的事情。这需要在实践中得到经验。我认为,先要找一个可以正常梯度下降的最大的learning rate,这样首先可以保证梯度可以正常地下降,其次训练速度也不会慢;但是这样意味着无法接近到cost function的最小值。在此时梯度逐渐收敛时,减小learning rate,继续训练,然后收敛,然后减小learning rate...循环往复。最终会接近cost function的最小值(同学们,我这加粗部分说的对不对,你们关于学习率的经验请分享一下吧)
吴恩达也介绍了相关经验,他是从0.001,0.003,0.01,0.03,...,0.3,1这样3倍一提升来寻找learning rate,可以作为实战中的参考。
慢着,等等,此时我好像反应过来一些什么,求cost function的最小值?最小值怎么求,不应该是一阶导等于0吗?让一阶导等于0的θ不就是我们想要的θ吗,还辛苦的梯度下降干啥。
确实,这种方式可以求出来我们要的θ,并且连求一阶导的功夫都省了,下边公式可以直接求出来θ。他叫做Normal Equation(标准方程)。
(其中X是第一列为1,从第2列起为所有特征值组成的矩阵,就是θ 0x 0 + θ 1x 1 + θ 2x 2中[x 0,x 1,x 2]这样的矩阵,x 0为全1,Y是label组成的矩阵)
并且这样求θ都不用上边讲的Feature Scaling呢。
这东西这么好还用梯度下降干啥呢?它真的就是最好的吗,请看下表:
从第3行的时间复杂度我们可以看出一些端倪。在n不大的时候,用上边的公式确实不错。当n也就是特征的数量很大的时候,Normal Equation的n3的“威力”就会显现出来了。速度慢。
In practice, when n exceeds 10,000 it might be a good time to go from a normal solution to an iterative process.
然而学过线性代数的同学们都知道,并不是任何一个矩阵都是可逆的,如果一个矩阵不可逆,Normal Equation的逆矩阵就没法求,这个方法也就不能用了。虽然说计算是可以用捷径计算出来的,见下边英文...(注:octave类似matlab)
When implementing the normal equation in octave we want to use the 'pinv' function rather than 'inv.' The 'pinv' function will give you a value of θ even if XTX is not invertible.
就是说在octave里编程计算时,用pinv函数代替inv函数求逆,就算是不可逆矩阵,也能求出来。但是是伪逆。
对于无法求逆的矩阵,一般来说有以下办法:
虽然说学过线性代数,大部分其实也还给了老师,什么有逆矩阵的充要条件啊,谁还记得。但是自己想一想,也能有个八九不离十。例如我的数据集中存在如下两种特征,平方米面积,平方英尺面积。这两个分明就是可以进行换算的,远看是两个特征,近看还是两个特征,实际上是同一个特征的情况。这种情况是不是就对应着矩阵中存在线性相关?所以说解决办法也很简单,删除其中一个特征就好了。
还有一种情况,特征数量多,多于训练样本数量。同学们想想,我用10条样本拟合出100个特征,这可能吗?所以还是删除一些作用不大的特征吧。我记得在之前哪篇文章里讲过筛选特征来着?那个信息增益?
好了,太晚了,睡了。
最后,文章首尾呼应,强烈推荐一部网剧,《河神》
参考资料:吴恩达机器学习
如果你也喜欢机器学习,并且也像我一样在ML之路上努力,请关注我,我会进行不定期更新,总有一些可以帮到你。
部分图片来自网络,部分本人绘制